В приведенном примере с равномерным законом распределения плотности вероятности исходная, или безусловная, энтропия как до, так и после измерения, составляет
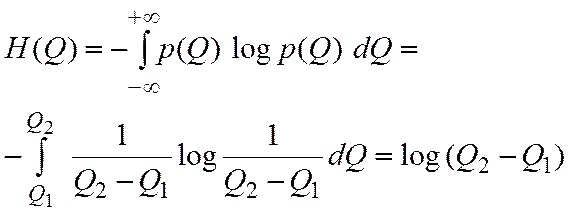
Оставшаяся после получения отсчета Qп условная энтропия равна:
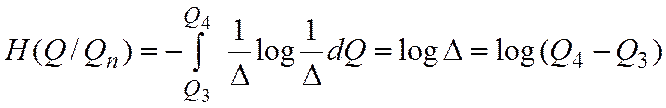
Полученное количество информации, равное разности исходной (безусловной) и оставшейся (условной) энтропий определяется как
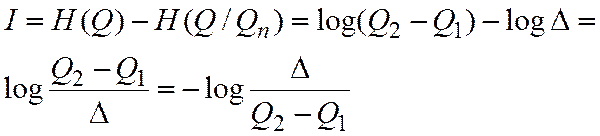
В замене операции деления D на Q2 – Q1 , используемой в классической (ортодоксальной) метрологии при определении относительной погрешности измерения, на операцию вычитания исходной и оставшейся неопределенностей, характеризуемых соответствующими значениями энтропии, и заключается основной прием анализа теории информации.
9. Измерение как сужение интервала неопределенности
Рассмотрим понятия однородных величин, шкалы порядка (реперной шкалы), шкалы интервалов, шкалы отношений, измерительного преобразования.
Различные предметы могут сравниваться между собой лишь по однородным свойствам. Под однородными свойствами и характеризующими их величинами понимают такие, которые могут быть сопоставлены между собой по признаку “больше – меньше”.
Сопоставляя предметы друг с другом, мы обнаруживаем признаки их отличия, например: данный предмет тяжелее или легче другого, тверже или мягче, теплее или холоднее длиннее или короче и т.п. Разложим предметы в ряд так, чтобы каждый последующий был тверже предыдущего, или таким же образом, но по какому‑либо другому признаку, относительно которого такое разложение предметов возможно. Однородными называются сравнимые по признаку “больше ‑ меньше” величины, которые могут быть расположены в последовательный ряд, составленный так, что каждая из входящих в него величин будет больше всех предыдущих и меньше всех последующих.
После того, как возможные значения измеряемой величины расставлены по признаку “больше ‑ меньше” в последовательный ряд, последующей предпосылкой для возможности производства измерений является выбор некоторых из этих значений в качестве отправных (по-французски реперных) точек. Совокупность выбранных реперных точек образует некоторую “лестницу” или шкалу (от латинского scalae – лестница) возможных значений измеряемой величины. Подобные шкалы называют шкалами порядка. Так, для измерения скорости ветра, что было необходимо для парусного флота, в 1805 г. Бофортом была предложена шкала скорости ветра в “баллах Бофорта”, представленная в методических указаниях к выполнению контрольной работы (раздел 4 данного УМК).
С развитием техники измерений шкалы порядка заменяются на шкалы интервалов и шкалы отношений. Так, шкала Бофорта использовалась до 1964 года, когда международным соглашением был принят ее перевод в скорость ветра, измеряемую в метрах в секунду. Это не меняет принципиального значения шкал порядка, так как во многих случаях они являются единственно возможной шкалой для производства измерений. Примером последнего случая может служить используемая до настоящего времени минералогическая шкала твердости. Твердость – это свойство вещества сопротивляться проникновению в него другого тела, вызывающего изменение или повреждение его поверхности. Это свойство имеет все признаки однородной физической величины, так как к нему в полной мере применимо понятие “больше – меньше”: Более твердые тела без особого труда отличаются от менее твердых тел. Однако метода построения шкалы интервалов или шкалы отношений для твердости природных материалов до сих пор нет, и существующая шкала твердости “в баллах” остается единственной шкалой твердости минералов.
Если под измерением понимать лишь сравнение измеряемой величины с некоторым значением, принятым за единицу, то измерения по шкалам порядка, в которых еще нет постоянной единицы измерения, придется рассматривать как нечто “недостойное” называться измерением. В классической метрологии, оперирующей понятием погрешности измерения, так и поступили, назвав измерения по шкалам порядка “грубой оценкой” или просто “оценкой”. Последнее время вместо термина “оценка” иногда применяется термин “мягкие измерения”.
Однако в действительности эта оценка может быть не так уж и груба. Так, например, если нам в результате опыта стало известно, что измеряемая температура была такова, что серебряный образец уже расплавился, а золотой еще оставался твердым, то значение температуры, следовательно, находилось в интервале от 960,5 до 1063 оС. Используя средство измерений класса точности 5 и, получив показание, равное 1010 оС, получим интервал неопределенности 2(1010х0,05) = 101 оС, равный интервалу между реперными точками. Таким образом, информация, полученная в результате измерения по шкале порядка, ничем не хуже той, которая может быть получена при использовании других измерительных устройств соответствующего класса точности.
Основным недостатком шкал порядка является полное отсутствие уверенности в том, что интервалы между выбранными реперами являются равновеликими. Именно таково, например, положение со шкалой Бофорта. Неравенство протяженности баллов шкалы Бофорта между собой показано в последнем столбце таблицы (в разделе 4 УМК).
Получение любой информации, в том числе и измерительной, теория информации трактует как устранение некоторой части неопределенности, а количество информации определяется как разность неопределенностей ситуаций до и после получения данного сообщения.
В случае измерения по шкале порядка весь диапазон возможных значений измеряемой величины разбивается реперными точками на ряд интервалов. Неопределенность до измерения характеризуется тем, что мы не знаем, в каком из интервалов лежит значение измеряемой величины, т.е. область неопределенности до измерения простирается на все интервалы шкалы порядка (от “штиля” до “урагана” по шкале Бофорта или от “мягче талька” до “тверже алмаза” по минералогической шкале т т.д.). В результате измерения появляется указание того, что измеряемая величина лежит в конкретном интервале, т.е. область неопределенности сужается от полной длины натуральной шкалы до длины указанного интервала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.