Если стоит задача оценить энергетическое действие электрического тока, мгновенное значение которого не остается постоянным во времени, то используется функционал
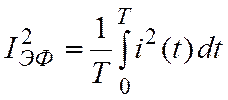(10.1)
Аналогом этого квадратичного функционала в теории вероятности является функционал для дисперсии, а аналогом действующего значения переменной составляющей тока – понятие среднеквадратического отклонения случайной величины.
Характеристикой транспортной способности тока с произвольной формой кривой при переносе вещества (например, в электролитической ванне) является его среднее значение
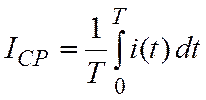(10.2)
Аналогом такого линейного функционала в теории вероятностей применительно к процессу измерения является определение интервала неопределенности с помощью квантильной оценки с заданной вероятностью. За интервал неопределенности принимается интервал, в который попадает определенный процент всех наблюдаемых отсчетов.
Разница между этими двумя усредненными значениями тока может быть весьма существенной и зависит от формы кривой его изменения во времени. Если функционал (10.1) неправомерен для описания переноса вещества, а функционал (10.2) для описания транспортировки энергии, то для характеристики процессов “транспортировки информации” должен существовать свой, особый функционал.
Исходя из многолетнего опыта установления интервала неопределенности, остающегося после выполнения измерения, следует, что этот интервал не имеет однозначного соотношения с оценкой среднеквадратического отклонения s. Оценка мощности помехи не определяет однозначно ее мешающее, дезинформирующее воздействие. Если закон распределения результата измерения при непрерывном отсчете считают близким к равномерному закону, интервал неопределенности принимают равным всей ширине этого распределения. Внутри интервала все отсчеты равновероятны, доверительная вероятность PД = 1. В случае нормального закона распределения вероятности указать интервал неопределенности простым логическим рассуждением нельзя. Пологое распределение можно охарактеризовать только среднеквадратическим отклонением, значения максимального отклонения указать нельзя, так как при таком распределении теоретически, хотя и редко, но могут встречаться сколь угодно большие отклонения. Если относительное среднеквадратическое отклонение при нормальном законе распределения d = 0,5% , то в среднем на каждые три отсчета будет попадаться одно отклонение, достигающее 0,5% , на каждые 22 отсчета в среднем будет встречаться одно отклонение, достигающее 2d = 1%. Один раз на 370 или 15000 отсчетов будут встречаться отклонения 1,5 и 2% . Приходится определять интервал неопределенности, приписывая ему некоторое значение td. Если принимать t равным 1, 2, 3, то получим доверительные интервалы при доверительной вероятности 0,67, 0,95 или 0,997.
Таким образом, не пользуясь теорией информации обоснованно выбрать ширину интервала неопределенности, остающегося после выполнения измерений, представляется затруднительным.
Согласно выражению (8.1) количество информации, получаемое в результате измерения, равно разности энтропий до и после проведения измерения. Исходная неопределенность H(Q ) зависит только от распределения вероятностей различных значений измеряемой величины (различных сообщений). Неопределенность, остающаяся после измерения, т.е. условная энтропия H(Q/Qп.), зависит только от распределения вероятностей помехи. Поэтому каждый из членов основного соотношения теории информации может рассматриваться отдельно и независимо друг от друга.
В связи с этим дезинформационное действие шума или помехи зависит только от их закона распределения и может быть однозначно указано путем вычисления энтропии H(Q/Qп.) этого закона распределения. Таким образом, по Шеннону единственным эффективным критерием дезинформационного действия любого шума или помехи является их энтропия.
Исследуя дезинформационное действие помех с различными законами распределения вероятностей, Шеннон обнаружил, что однозначного соответствия между мощностью помехи (т.е. ее дисперсией s2 ) и вносимой ею дезинформацией (т.е. значением энтропии) не наблюдается. При одной и той же мощности помехи вносимая ею дезинформация различна и зависит от закона распределения вероятностей этой помехи. При определенном среднеквадратическом значении (при определенной мощности) помехи наибольшим дезинформационным действием (наибольшей энтропией) обладает помеха с нормальным законом распределения вероятностей. При любом другом законе распределения вероятностей помехи ее энтропия (при том же самом среднеквадратическом значении) оказывается меньшей.
Таким образом, при произвольном законе распределения вероятностей дезинформирующее действие помехи определяется не всей мощностью помехи, а только ее некоторой частью, которую Шеннон назвал энтропийной мощностью помехи. По аналогии с дисперсией и среднеквадратическим отклонением при исследовании процессов получения измерительной информации удобнее оперировать не энтропийной мощностью помехи, зависящей от степени воздействия возмущающих факторов, а энтропийным значением неопределенности.
Для более полного рассмотрения энтропийного значения неопределенности, остающейся после выполнения измерения, определим энтропию для рассмотренных выше равномерного и нормального законов распределения вероятности.
Для непрерывной случайной величины значение условной энтропии определяется выражением:
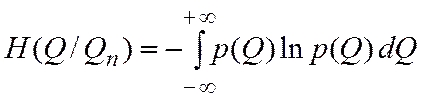
Плотность вероятности p(Q) для равномерного закона распределения (рис.8.2) может быть записана по участкам
p(Q ) = 0 при Q < Q3 иQ > Q4
p(Q ) = 1/D при Q3 < Q < Q4
Отсюда условная энтропия при равномерном законе распределения равна
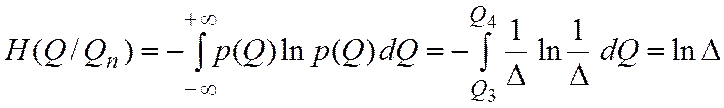
Из этого выражения видно, что условная энтропия равна логарифму интервала неопределенности или, наоборот, значение интервала неопределенности есть величина, стоящая под знаком логарифма в выражении для условной энтропии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.