Используя связь между энтропийным значением неопределенности и среднеквадратическим отклонением результата измерения через энтропийный коэффициент К в виде D = 2Кs, можно получить ряд упрощенных способов определения энтропийного интервала неопределенности, получаемого после выполнения измерения. Большая серия отсчетов необходима лишь для установления вида закона распределения, т. е. для определения величины среднеквадратического отклонения s и энтропийного коэффициента К.
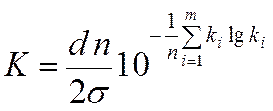
При вычислении энтропийного значения неопределенности для ряда однотипных измерений, при которых используются однотипные средства измерений и однотипные методики выполнения измерений, обстоятельное исследование (50 – 200 отсчетов) может быть проведено один раз с целью установления значений К и s . Далее предполагают эти значения неизменными и используют их в качестве априорной информации при выполнении однократного измерения. При выполнении многократного измерения с ограниченным числом отсчетов (10‑15), значение s определяют на основе экспериментальных данных, полученных при конкретном измерении, а значение К используют на основе априорной информации.
В приложении 3 (в методических указаниях к выполнению контрольной работы) приведена таблица для значений ki lg ki , используемых при вычислении энтропийного значения неопределенности результата измерения и энтропийного коэффициента в соответствии с приведенными выше формулами.
Для использования априорной информации о виде распределения экспериментальных данных имеет большое значение накопление данных и составление каталогов о видах распределения, характерных для различных типов средств измерений и широко применяемых методов измерений.
Реальные значения энтропийного коэффициента для большинства средств измерений, применяемых при выполнении технических измерений, близки к энтропийному коэффициенту равномерного распределения. В случае использования информации о классе точности средства измерения, при определении неопределенности результата измерения принимают математическую модель равномерного закона распределения.
Как показано в работах профессора П. В. Новицкого, упрощенный метод определения энтропийного интервала неопределенности на основе известного значения s состоит в принятии условия d =2s (К = 2).
12. Информация в метрологических системах
Понятие «система» является распространенным, относится к наиболее обобщенным и применяется к самым разнообразным объектам изучения. В метрологии термин «система» также получил широкое распространение. Например в таких словосочетаниях, как «система единиц», «система эталонов», «система метрологического обеспечения» и т.п. Профессором Слаевым В.А. введено обобщающее понятие «метрологической системы» как системы (определенной) категории объектов, изучаемых в метрологии. Эти объекты разнообразны и могут быть как материальными (средства измерений, эталоны, обеспечивающие технические средства и т. д.), так и нематериальными (термины и определения, обозначения единиц физических величин и их определения, содержание нормативных документов, протокольная документация и т.д.), а также смешанного типа (методы и средства поверки, определения единиц и их воспроизведение, метрологическое учреждение в целом и т. д.).
Средства измерений служат для получения количественной информации о наиболее существенных свойствах объектов, поэтому каждое средство измерений может рассматриваться как канал передачи и преобразования информации об измеряемой величине. Приемником сообщений служит человек, ПЭВМ, средства для дальнейшей обработки информации и обеспечения информационных процессов. Источником сообщений (информации) служит объект измерений. Сообщение, поступающее от объекта измерений, содержит информацию о размере физической величины, характеризующей исследуемое свойство объекта. Копия сообщения содержит получаемую измерительную информацию.
Формы представления измерительной информации зависят от ее предназначения. Если измерительная информация предназначена для дальнейшей переработки, то она представляется в виде закона распределения вероятности результата измерения или его числовых характеристик (оценок). Если измерительная информация не предназначена для дальнейшей переработки, то она представляется в форме, удобной для человека.
Как было показано выше, количество информации, полученное в результате измерения, равно разности исходной и оставшейся энтропий, что приводит к выражению
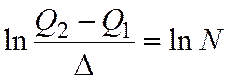 ,
(12.1)
,
(12.1)
где число N = (Q2 – Q1) / (D) показывает, сколько интервалов неопределенности длиной D = 2d укладывается во всем диапазоне Q2 – Q1, т. е. какое число различимых градаций измеряемой величины позволяет получить данное средство измерений или методика выполнения измерений.
Соотношение (12.1) справедливо при любом законе распределения вероятности, если только интервал неопределенности Dбудет найден через энтропию. Величина N именуется числом различимых градаций измеряемой величины. Сам термин введен в середине прошлого века П.А. Новицким на основе анализа работ Л. Бриллюэна. Смысл вводимого понятия можно пояснить на рис. 12.1.
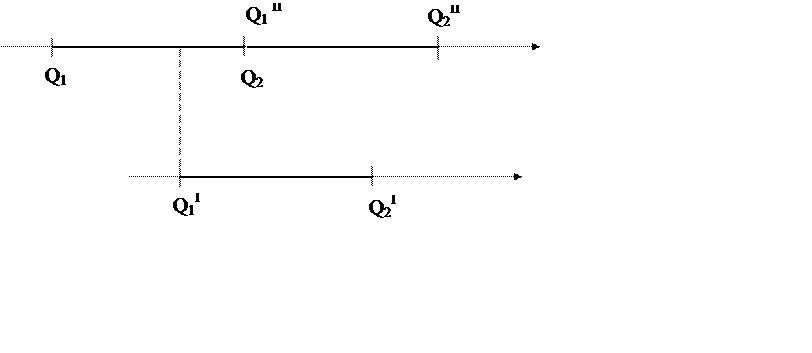 |
Рис. 12.1. Иллюстрация к понятию «число различимых градаций».
Пусть в результате измерений получены интервалы неопределенности Q2‑ Q1, Q2I– Q1I, Q2II– Q1II. В случае первого и второго интервала нет возможности утверждать, что измерялись однородные величины разных размеров, поскольку полученные интервалы пересекаются. В случае первого и третьего интервалов можно говорить о том, что измерялись величины разных размеров.
Число различимых градаций N измеряемой величины зависит от класса точности средства измерений. Поясним сказанное на примере шкалы гипотетического амперметра, изображенной на рис. 12.2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.