Предел измерений амперметра 20 А, класс точности – 5. Для указанного прибора измеряемая сила электрического тока не может отличаться от того, что показывает указатель(стрелка), больше чем на 1 А. Если стрелка остановилась на делении 9, то значение измеряемой величины может находиться в пределах от 8 до 10. Число N различимых градаций в данном случае составляет:
N = 100/2|кл.точ.| = 10 или N = 20 А/2 А
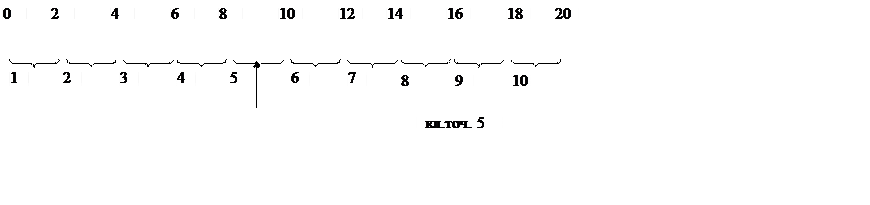 |
Рис. 12.2. Зависимость числа различимых градаций от класса точности средства измерений
В данном случае используется ситуационная модель, предполагающая, что в пределах полученного интервала имеет место равномерное распределение плотности вероятности.
Количество полученной информации I =log10.
Примечание: альтернативный подход предусматривает, что в начале шкалы слева от 0 может быть деление – 1. Тогда число различимых градаций 11. Этот подход, принятый рядом зарубежных метрологов не принят в России исходя из энергетической теории СИ.
При единичных измерениях, выполняемых обычно с помощью стрелочных приборов, определение среднего количества информации оказывается невозможным. Во многих других случаях – анализе и определении неопределенностей измерений, экспертном оценивании методов измерений, при цифровых измерительных технологиях, обработке и передаче полученных при измерении данных (как и при непрерывных измерениях быстропротекающих процессов) целесообразно использовать методы теории информации. Рассмотрим некоторые положения и понятия теории информации, связанные с фактором времени. Если каждое отдельно измеренной значение из n статистически независимых значений, образующих определенное количество Минформации, содержит среднее количество информации Iср, то эти величины можно связать между собой следующим соотношением:
M = nIср (12.2)
Для случая равномерного распределения значений, представляемых m уровнями,
Из последнего соотношения можно сделать важные качественные выводы: количество информации (информативность) измерений возрастает с увеличением количества измерений (числа отсчетов) наблюдаемой величины и числа различимых ступеней ее квантования.
Количество информации, получаемое в единицу времени, определяется как поток информации, или производительность источника, и измеряется в единицах [M] = бит/с.
По аналогии с выражением (12.2) можно записать:
M =(dn/dt) Iср
Если именуемое временем установления показаний, или тактом, время, необходимое для получения (передачи) одного измеренного значения (dn = 1), обозначить через ТИ, то можно средний поток информации определить следующим образом:
M = (1/TИ) Icр (12.4)
Максимально возможный поток информации СК, передаваемый через канал связи, называется емкостью канала связи и имеет также размерность единицы потока [CK] = бит/с. Под емкостью канала средства измерения (по аналогии) можно понимать максимально возможное количество информации, получаемое за определенное время. Так как число m различимых уровней квантования средства измерения (или число различимых градаций N) является определенным и постоянным, то емкость этого средства пропорциональна максимальному числу отсчетов nmax , полученному за указанное время, т.е. СК ~ nmax. В практике измерений этот предел обычно недостижим и М < СК. Сказанное можно пояснить следующим примером. Предположим, что используется электроизмерительный прибор класса точности 1,6 с временем установления ТИ = 0,8 мс. Емкость канала этого прибора, при допущении равномерного распределения измеряемых значений, составляет СК = 6,2 кбит/с, что доказывается следующим расчетом.
N = m = 1/(2|0,016|) = 31,25
Icp = log31,25 = 4,96
СК = (1/0,8 мс)х4,96 бит = 6,2 кбит/с.
Рассмотрим измерительный прибор, имеющий две шкалы – грубую и точную. Цена деления точной шкалы уменьшена по сравнению с грубой. В этом случае количество информации суммируются. Так как каждому делению грубой шкалы с числом делений m1 соответствует m2 делений точной шкалы, то общее число делений обеих шкал mизм, т.е. число возможных различимых уровней двухшкального измерительного прибора, составит:
mизм = m1m2
Если предположить, что интервал неопределенности результата измерения равен одному делению точной шкалы, то количество полученной информации
Iизм = I1+ I2 = logm1 + logm2
Проще всего уменьшить неопределенность информации, если решение заключается в выборе одного из двух значений или представляет собой высказывание типа “Да” или “Нет”. В измерительной технике подобные решения связаны с определением двух граничных значений. Примером может служить определение уровня электропроводящей жидкости в резервуаре (рис. 12.3). При погружении в жидкость электрода, соединенного с катушкой определенного реле, последнее срабатывает и загорается соответствующая лампа, “отвечая” утвердительно на вопрос: “Уровень жидкости Врез ³ 0,25В0?”.
Для подобного рода решений число различимых значений величины m =2 и вероятность появления одного из значений этой величины p0=0,5. Однозначный ответ на подобного рода вопрос представляет собой единицу количества информации – бит. Для определения уровня жидкости необходимо задать два вопроса, в результате чего будет получена информация I = 2бит, что иллюстрирует табл.12.1.
Таблица 12.1
Возможные состояния уровня жидкости в резервуаре.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.