Использование основных положений теории информации для характеристики процесса измерений, страница 6

Величина интервала неопределенности может быть выражена также через среднеквадратическое отклонение. Для равномерного распределения

Q₃ – Q_п.= ‑ 0,5D,      Q₄ – Q_п. = + 0,5D

Обозначим 0,5D = d, тогда для центрированного равномерного закона дисперсия составит

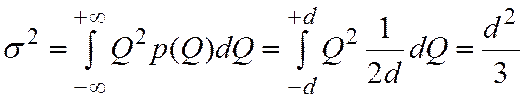                   (10.3)

Таким образом, для равномерного закона распределения , . Интервал неопределенности . Следовательно, энтропия

Обозначим для центрированного нормального закона распределения , тогда при СКО равном s,

,

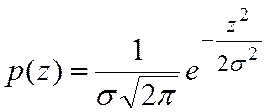а условная энтропия, т.е. неопределенность, оставшаяся после измерения, равна

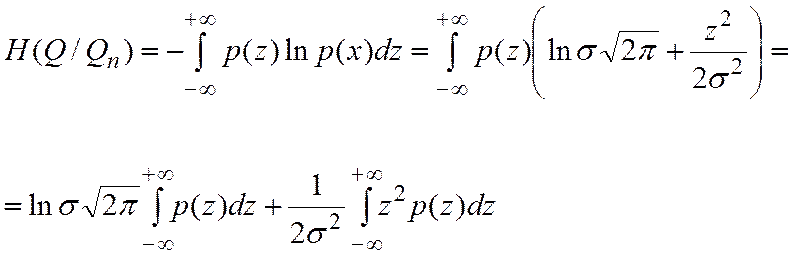
Так как

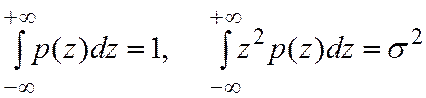
то

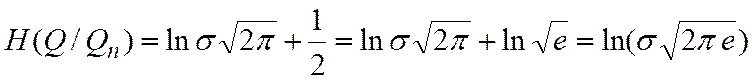.        (10.4)

Полученное выражение для нормального закона распределения вероятности отличается от полученного ранее выражения для равномерного закона распределения только выражением, стоящим под знаком логарифма. Отсюда вытекает важный вывод о том, что с информационной точки зрения неограниченное распределение вида пологой кривой приводит к получению точно такого же количества информации, как и резко ограниченное равномерное распределение, если соблюдается условие . Иными словами, эффективный интервал неопределенности, вызываемый разбросом показаний с пологой кривой распределения, совершенно эквивалентен по количеству вносимой дезинформации интервалу неопределенности, вызываемому равномерным и резко ограниченным распределением.

Изложенный подход к определению эффективного (в энтропийном смысле) интервала неопределенности может быть использован при любом законе распределения, характеризующем разброс показаний. Подобно тому, как понятием действующего значения электрического тока пользуются при любой форме кривой этого тока. Аналогичными могут быть и словесные определения этих обоих понятий.

Так, эффективным значением данного переменного тока мы называем значение постоянного, не изменяющегося во времени электрического тока, который производит такое же энергетическое действие, как и данный переменный ток. Подобно этому энтропийным значением неопределенности считается неопределенность такого равномерного распределения, которое вносит такое же дезинформирующее действие, что и данный закон распределения.

На рис. 10.1. приведен пример энтропийного значения неопределенности для равномерного, треугольного и нормального законов распределения.

Зависимость между энтропийным интервалом неопределенности и СКО может быть представлена как 0,5D = d = Ks, где коэффициент К зависит от вида закона распределения и называется энтропийным коэффициентом неопределенности или энтропийным коэффициентом закона распределения вероятности.

Как показал Шеннон, наибольшей энтропией при заданном значении мощности, т. е. наибольшим помехосодержанием, из всех возможных законов распределения вероятности обладает нормальное распределение. Поэтому оно имеет наибольший энтропийный коэффициент. Согласно (10.4) для нормального ЗРВ

Любое другое распределение, отличное от нормального, может иметь энтропийный коэффициент, только меньший этого значения. Например, согласно (10.3) для равномерного ЗРВ

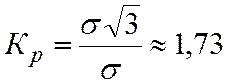
В обратном случае, если задано s (или аналог СКО – u), то наименьший интервал неопределенности характерен для равномерного ЗРВ.

 

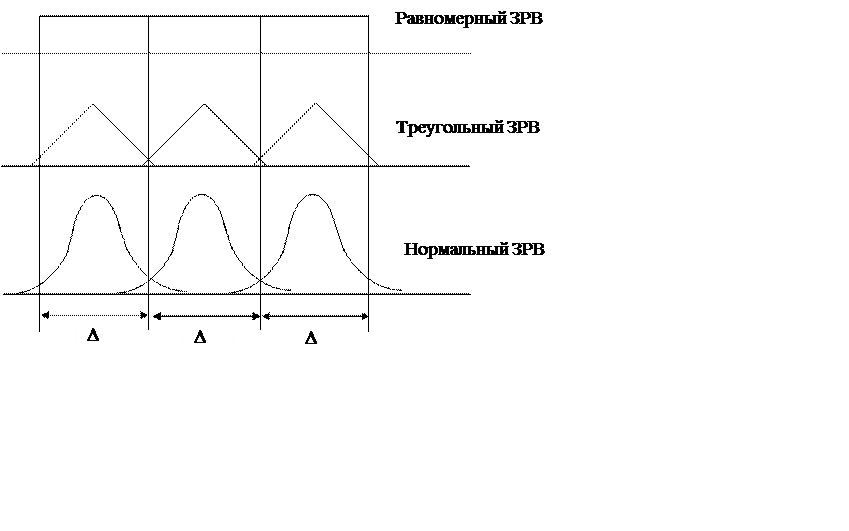Рис. 10.1. Пример соотношения энтропийного значения неопределенности для равномерного, треугольного и нормального законов распределения

11. Практические методы определения энтропийного интервала неопределенности

Энтропийный интервал неопределенности вычисляется по значению условной энтропии H(Q/Q_п), зависящей от закона распределения вероятности результата измерения. Однако, при оценке точности результата измерения мы располагаем не самим законом распределения, а лишь некоторым конечным числом n конкретных показаний средства измерений, подчиняющихся этому закону. На основании этого ограниченного числа показаний может быть построена ступенчатая гистограмма, в той или иной мере приближающаяся к действительному закону распределения (рис.11.1). Поэтому практически желательно иметь формулу для вычисления энтропийного интервала неопределенности исходя из полученной эмпирическим путем гистограммы.

Если гистограмма состоит из m столбцов с границами Q₀, Q₁,… Q_m и каждый столбец шириной d = Q_i – Q_i+1 включает в себя k_i показаний, то плотность вероятности на протяжении каждого из столбцов остается постоянной и равна

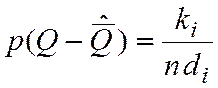
Энтропия такого ступенчатого распределения

 

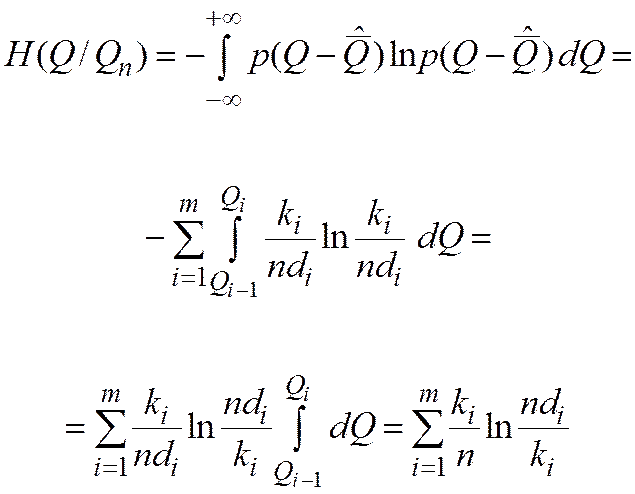
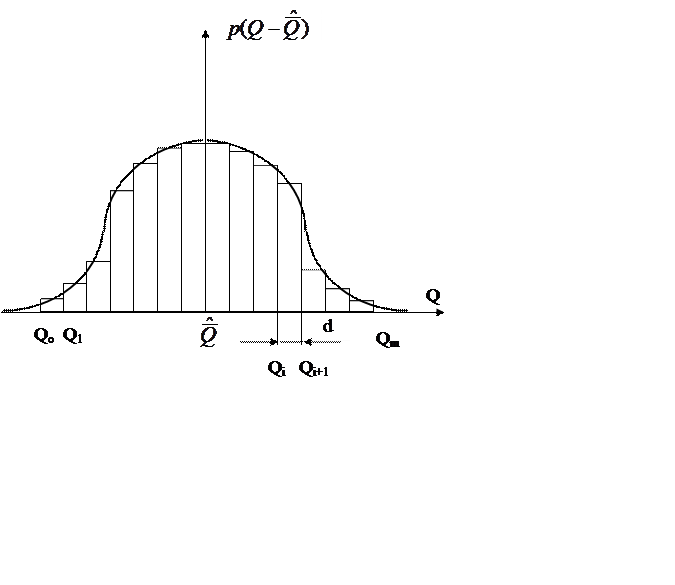Рис.11.1 Гистограмма на основе конечного числа показаний

Обычно ширина всех столбцов гистограммы принимается одинаковой, т.е. d_i = d , тогда

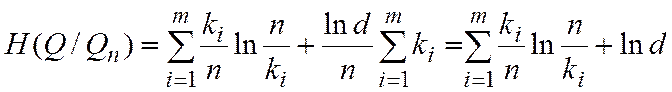
Таким образом, энтропия гистограммы определяется как взятая с обратным знаком сумма произведений вероятности случайной величины на логарифм этой вероятности, а член lnd обеспечивает независимость значения величины энтропии от произвольного выбора величины d ступеньки гистограммы.

Для расчетов это выражение можно представить как

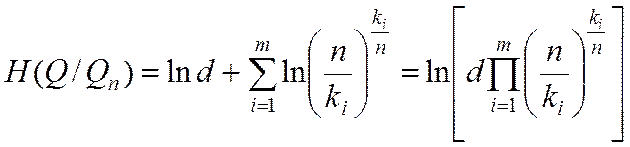
тогда энтропийное значение интервала неопределенности будет равно

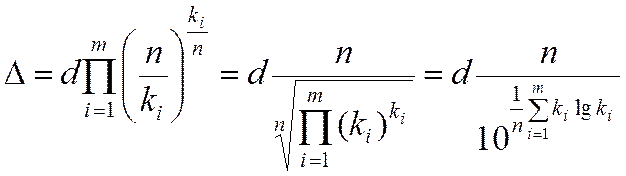              (11.1)

Исследование формулы (11.1) показывает, что полученная оценка является смещенной, но это смещение убывает по мере увеличения n и m. При этом m и d могут выбираться произвольно, но с ограничением k_i ³ 2 , так как наличие интервалов с k_i = 0 или k_i = 1 не изменяет энтропии, поскольку 1¹ = 1 и при определении энтропии полагают 0⁰ = 1.

Выражение (11.1) может быть использовано на практике только тогда, когда общее число показаний n настолько велико, что может быть разбито на m (не менее 5‑7) интервалов шириной d , в крайние из которых еще попадает по 2 показания. Это приводит к тому, что вычисление энтропийной неопределенности результата измерения, исходя из основного определения, можно выполнять, располагая серией не менее чем из 30‑50 наблюдений. Необходим такой объем испытаний, при котором уверенно определяется вид закона распределения вероятностей результата измерения. Поэтому метод прямого вычисления энтропийного значения неопределенности результата измерения может быть использован только при обстоятельных исследованиях, допускающих большую затрату времени.