Расчёт статически неопределимых систем (рам и балок): Методическое пособие

Мосиянова Е. И.

МЕТОДИЧЕСКОЕ  ПОСОБИЕ

По Сопротивлению материалов к разделу :

‘‘ РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ ’’

( рам и балок )

Рецензент                        Селиванов М. И.

Утверждено на заседании методического семинара

кафедры                      27/ IX - 85  г.

Утверждено на заседании методической

комиссии филиала          25/ X - 85  г.

Калуга      1985 г.

РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ

(  рам и балок )

ВВЕДЕНИЕ .

  Статически неопределимыми называются такие системы , для которых определение внешних реакций и всех внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия.

  Для простоты пояснений рассмотрим только те случаи, когда конструкция, и силы, действующие на неё, лежат в одной плоскости.

  Существует три типа плоских статически неопределимых систем : стержневые системы  c шарнирно связанными элементами ;  рамы и балки.

Системы первого типа в настоящем пособии не рассматриваются.

Рамой называется кинематически неизменяемая стержневая система, элементы которой жёстко связаны в узлах .

иногда в конструкцию рамы шарниры, но их введение не нарушает общей кинематической неизменяемости системы.

В рамах статическая неопределимость возникает :

1) за счёт большого числа внешних связей  (реакций опор)

(рис. 1а) - внешняя статическая неопределимость;

2) вследствие особенностей конструкции (наличие замкнутых контуров) (рис. 1б) - внутренняя статическая неопределимость;

3)  при наличии замкнутых контуров и  «лишних»  (  >3  )  внешних  связей  (рис. 1в).

     Балкой называется брус, работающий преимущественно на изгиб, причем длина его несоизмеримо больше двух других размеров, характеризующих поперечное сечение. У балок статическая неопределимость является следствием постановки дополнительных опор, обеспечивающих большую жёсткость системы. Такие балки принято называть неразрезными (рис.2)

рис. 2

Для рам и балок применим общий порядок раскрытия статической неопределимости.

1)  устанавливают степень статической неопределимости системы  (число «лишних», с точки зрения статики, неизвестных).

2)  получают основную и эквивалентную системы.  

3)  составляют канонические уравнения метода сил и решают.

4)  проверяют правильность полученного решения .

расчёт по этой схеме носит название «метода сил», поскольку в качестве «лишних» неизвестных выбирают усилия, действующие по направлению отброшенных связей.

I.   СТЕПЕНЬ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ СИСТЕМЫ.

I.   I  Статическая неопределимость рам.

Количество «лишних» связей в рамах определяется по формуле :

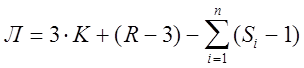                                                 , где

     К - число замкнутых контуров, каждый из которых имеет три неизвестных внутренних усилия (М - изгибающий момент, Q - поперечную силу, N - продольную силу) (рис. 3) R - число реакций внешних связей, 3 - число линейно независимых уравнений равновесия для плоской системы сил, n - число шарниров, S_i - число стержней, сходящихся в одном шарнире.

Рассмотрим статически неопределимую раму, представленную на рис.4. Для неё число замкнутых контуров равно 4 (I;II;III;IV), число внешних связей R=5 (три в за

                                                        рис. 4

щемлении А и по одной в тягах В и С). Эта рама имеет один шарнир (n=1), соединяющий четыре стержня (S-1)=4-1=3, 

Л=3 4+(5-3) - 1 (4-1) =11

Таким образом, рама 11 раз статически неопределима.

1.2. Статическая неопределимость балок.

Балка замкнутых контуров не имеет и для неё количество лишних неизвестных определяется по упрощённой формуле

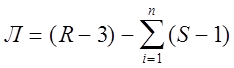                                                ,     S=2

Рассмотрим статически неопределимую балку (рис.5,а)

ри               рис.5.

Число внешних связей для рассматриваемой балки (R) равно 5 (три в опоре А и по одной на опорах В и С). В пролёте ВС имеется шарнир D, снимающий одну связь.

Тогда                                                           Л=5-3-1=1

Балка один раз статически неопределима.

Расчётная схема для такой балки представлена на рис. 5,б.

Дадим некоторые пояснения.

Так как изгибающий момент в шарнире равен 0,то через точку D могут передаваться только вертикальные усилия.

Следовательно, балка АС может быть представлена в виде системе, состоящей из двух балок: балки АВ и балки DC, которая в точке D опирается на балку АВ .

опора Dбалки DС является не подвижной шаровой опорой статически определимой балки DС. Реакции V_D, H_D  и V_D могут быть найдены с помощью уравнений статики, причём H_D = 0. Балка АВ, являясь один раз статически неопределимой, оказывается, в свою очередь, нагруженной внешними силами и реакцией V_D, приложенной в точке D.

2. ОСНОВНАЯ СИСТЕМА; ЭКВИВАЛЕНТНАЯ СИСТЕМА.

Основной системой называется статически определимая система, полученная из заданной путём отбрасывания «лишних» связей.

 Эквивалентной называется система, полученная, путём загружения основной системы заданными внешними силами и специально подобранными реакциями отброшенных связей, обеспечивающая такие же перемещения, как и заданной системе. Это достигается за счёт приравнивания к нулю перемещений точек приложения «лишних» связей по направлениям этих связей.   ;

D₁(P₁ ; P₂ ; ... X₁ ; X₂ ; ...) = 0                , т.е.

перемещение точки наложения первой связи по направлению этой связи от действия внешних сил (P₁ ; P₂ ;) и реакций «лишних» связей (X₁ ; X₂ ; ...) отсутствует.

Число таких уравнений равно числу таких отброшенных «лишних» связей.

2.1. Основная и эквивалентная система для рам.

При выборе основной системы для рам необходимо помнить, что статическая определимость является необходимым, но недостаточным признаком правильно выбранной основной системы.

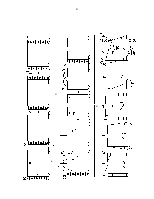
Рама, представленная на рис. 6,а, является 6 раз статически неопределимой.            

рис.6                                             

  Для неё можно предложить множество вариантов систем, некоторые из них представлены на рис. 6,б,в,г.

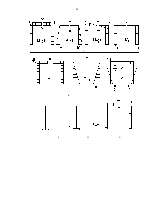
  Основная система выбрана правильно, если она обеспечивает кинематическую неизменяемость вновь полученной рамы и не включает в себя дополнительных связей, отсутствующих в заданной системе. Необходимо отметить, что недопустимо также и использование мгновенно кинематически изменяемых систем, подобно представленной на рис.7.

Связи, наложенные на систему допускают поворот рамы относительно точки А на малый угол. При этом реакция в опоре В достигает бесконечности. Для рассматриваемой рамы и предложенных основных систем (рис.6) эквивалентные системы будут выглядеть следующим образом (рис.8).