ж11. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ НА ИЗГИБ
Задачи, в которых число неизвестных силовых факторов и связей больше числа уравнений, называются статически неопределенными.
Метод сил.
Вместо отброшенных лишних связей мы прикладываем неизвестные (пока) силы.
|
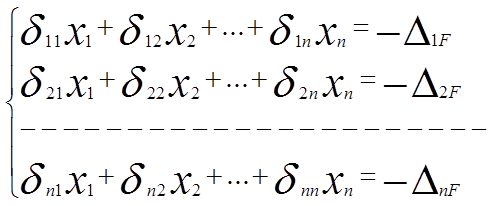
Порядок решения статически неопределенных задач:
1) Определить степень статической неопределенности.
2) Выбираем основную систему путем отбрасывания лишних связей, заменяем отброшенные связи неизвестными силами.
3) Составляем уравнения совместности дифференциации в виде канонических уравнений метода сил.
4) Решаем систему уравнений.
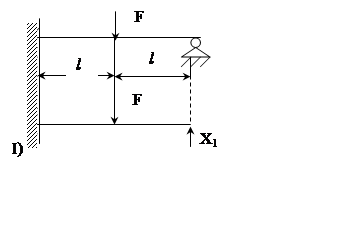 |
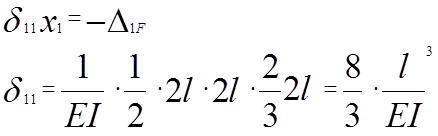
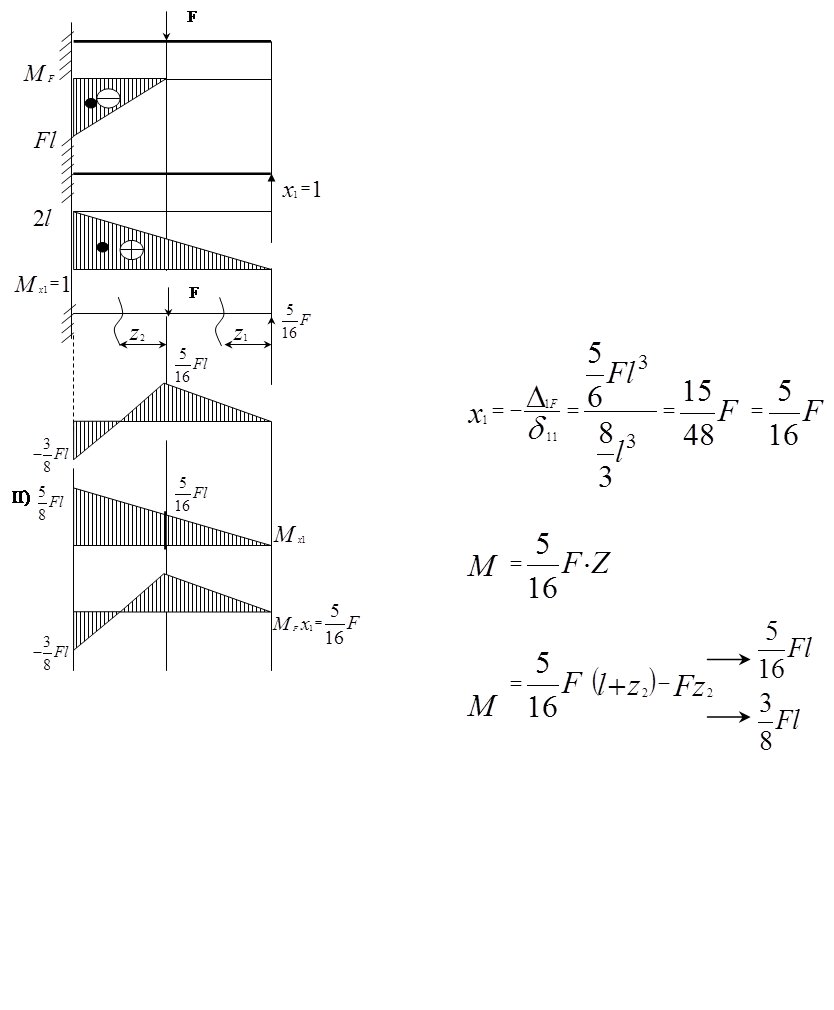
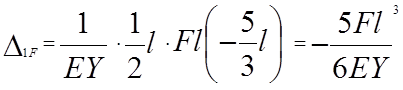
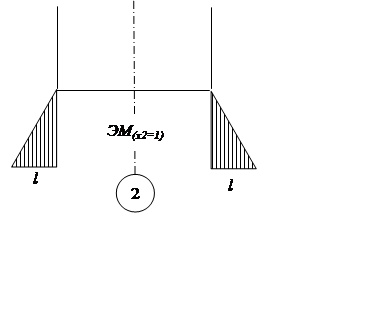
Задача 2. 4 – 3 = 1 (раз статич. неопред.)
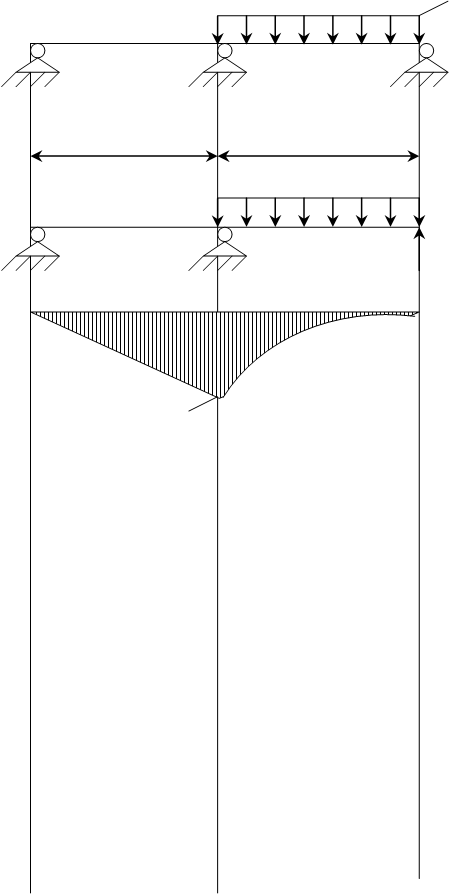 |
|||
|
|||
![]()
![]()
![]()
![]()
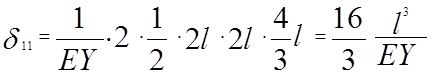
![]()
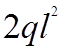
![]()
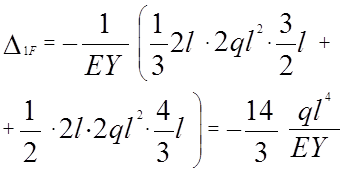
![]()

 |
|||
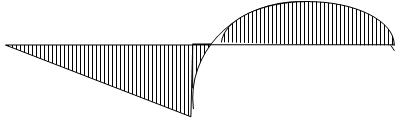 |
|||
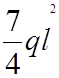
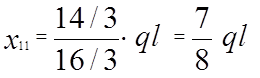
![]()
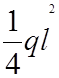
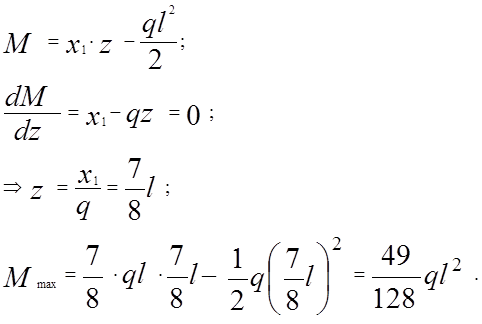
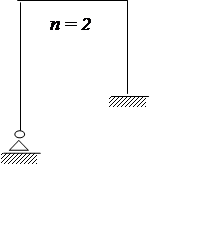
Статически неопределимые рамы
 |
|||||||||
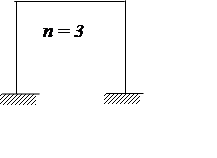 |
|||||||||
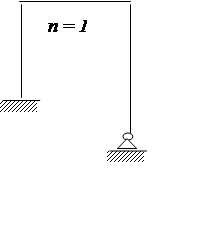 |
|||||||||
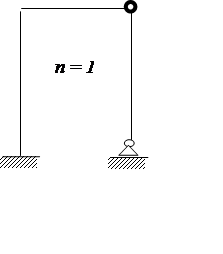 |
|||||||||
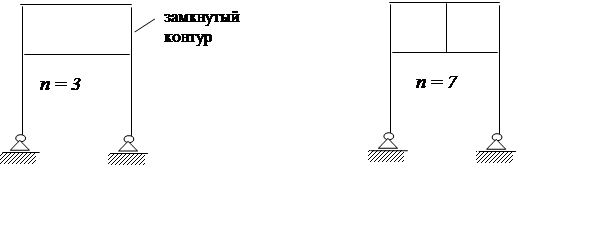 |
|||||||||
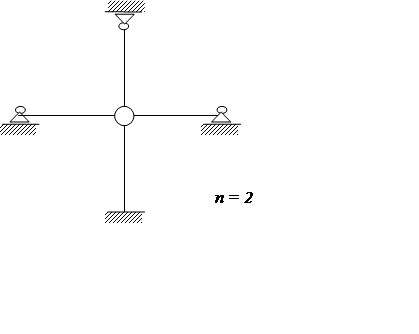 |
|||||
![]()
где R – количество реакций;
Ш – число шарниров;
К – количество замкнутых контуров;
S – число стержней, сходящихся в шарнире.
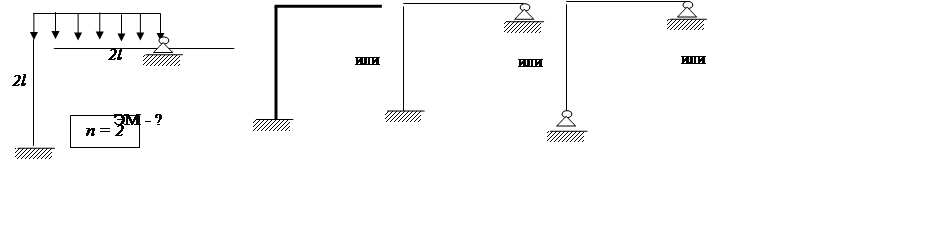 |
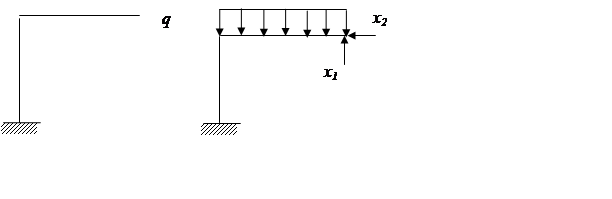 Основная система должна быть статически определима и
кинематически неизменима.
Основная система должна быть статически определима и
кинематически неизменима.
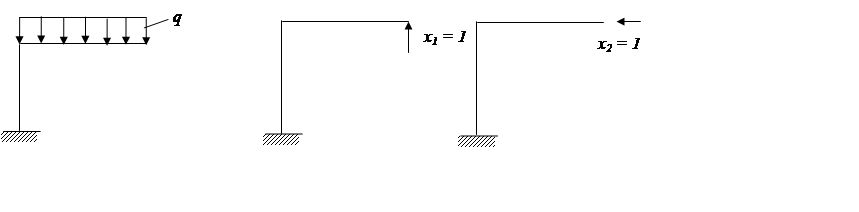 |
|||
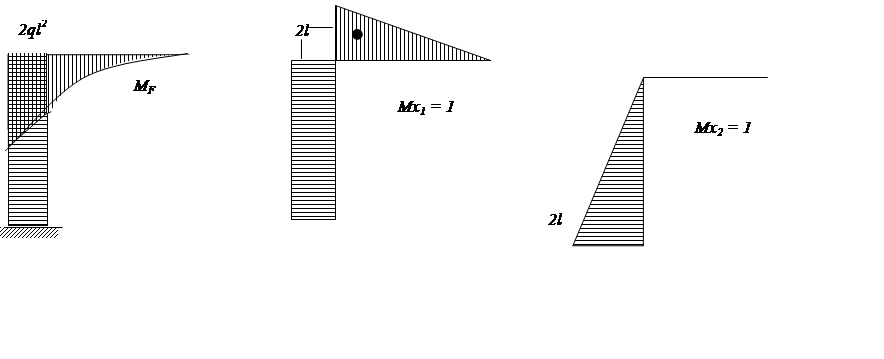 |
|||
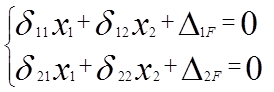
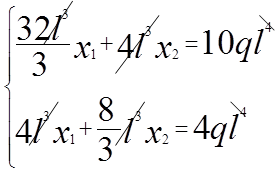 |
|||
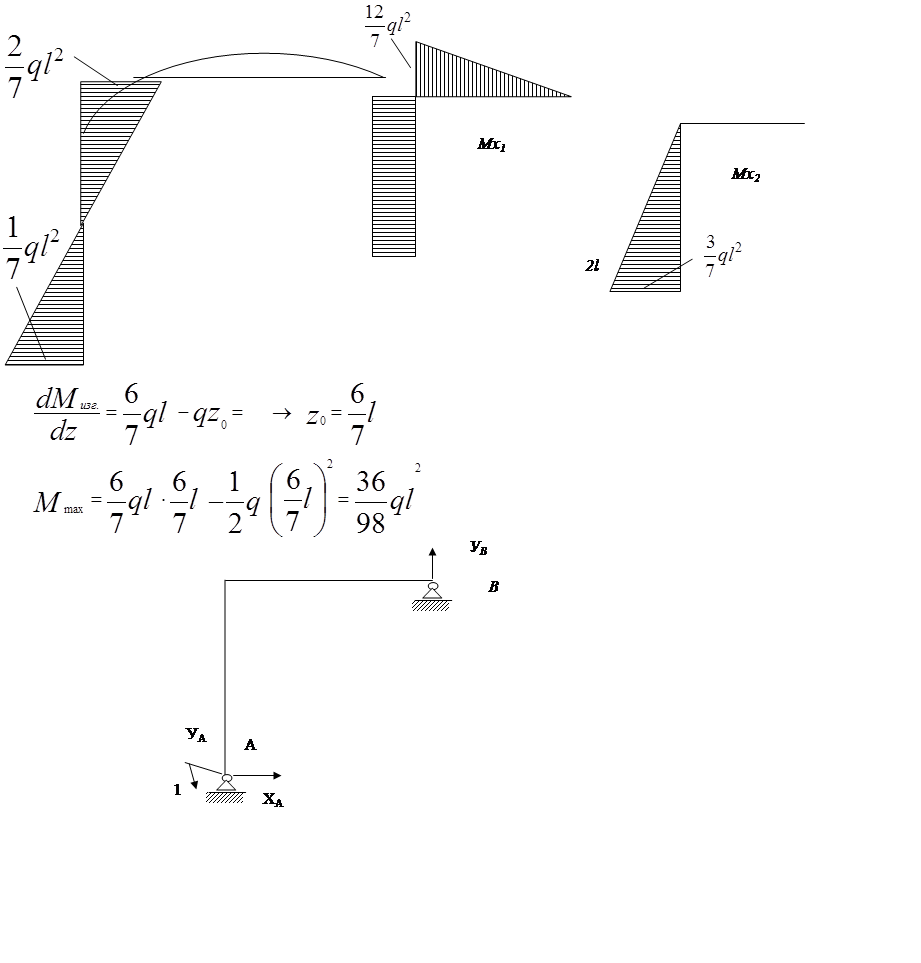 |
|||
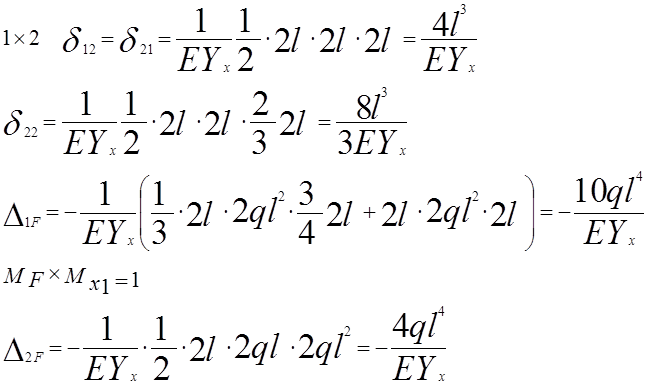
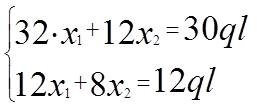
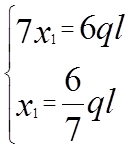
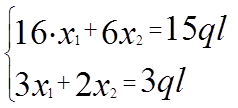
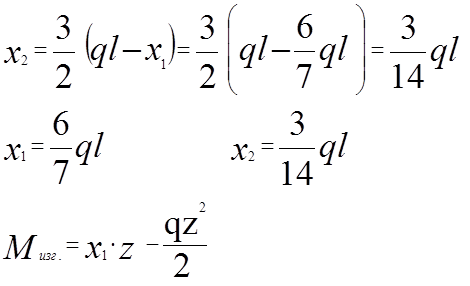

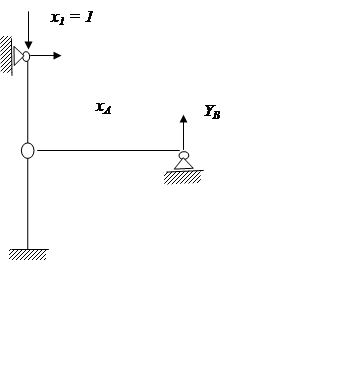
Проверка:
Выберем другую систему.
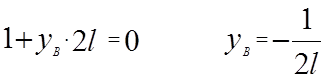 S Fx = 0, XA = 0
S Fx = 0, XA = 0
 S MA = 0:
S MA = 0:
S MB = 0:
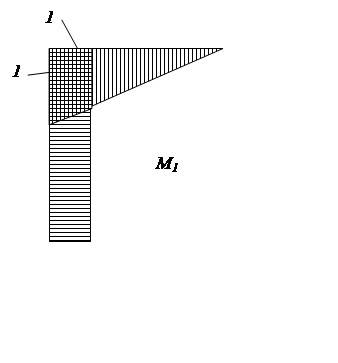 |
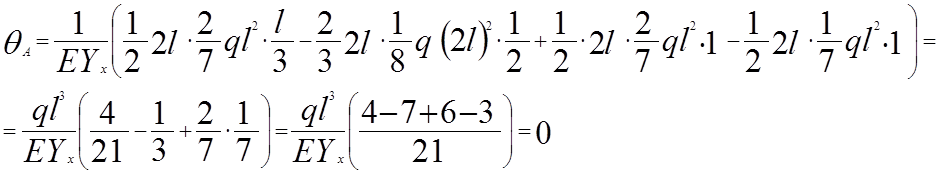
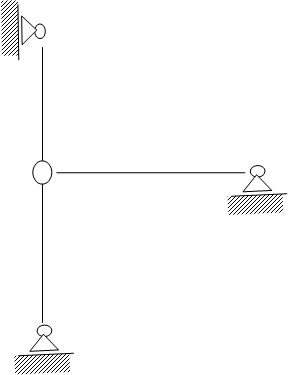 Задача:
Задача:
 |
|||
 |
|||
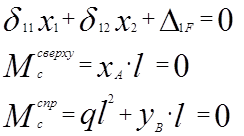
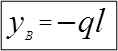
![]()
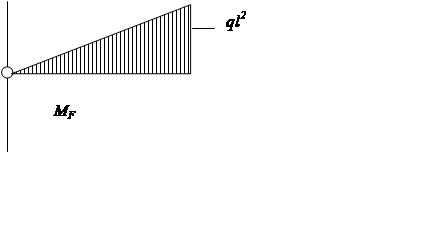 |
||
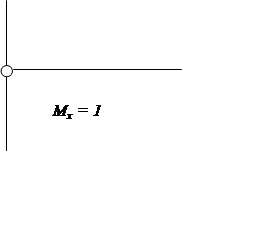 |
||
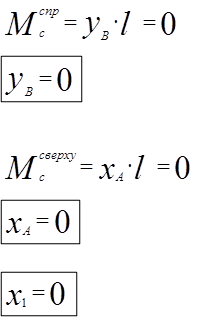
статической неопределенности
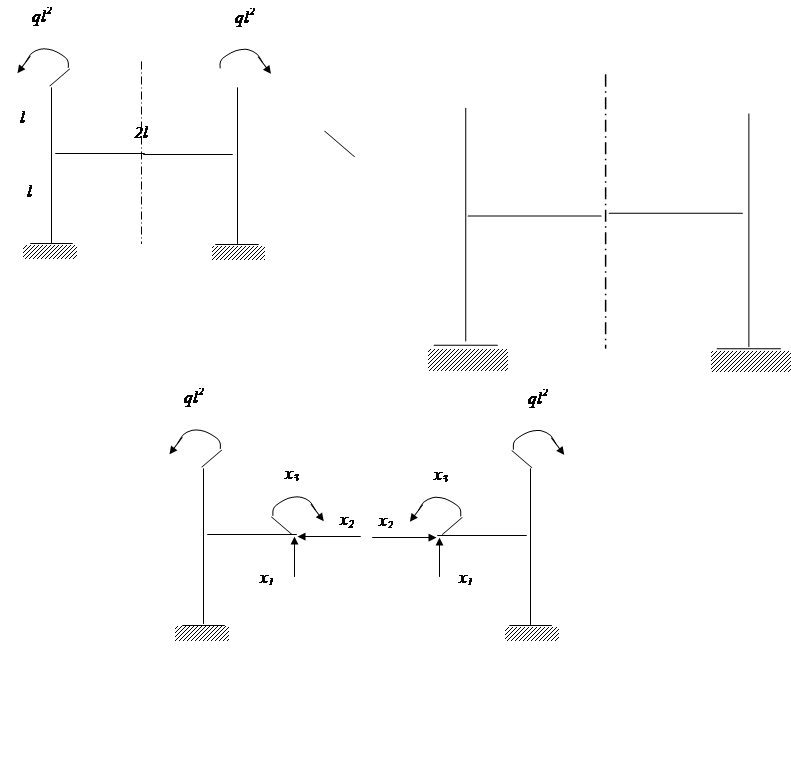 |
n = 3
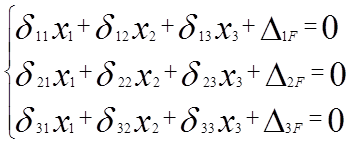
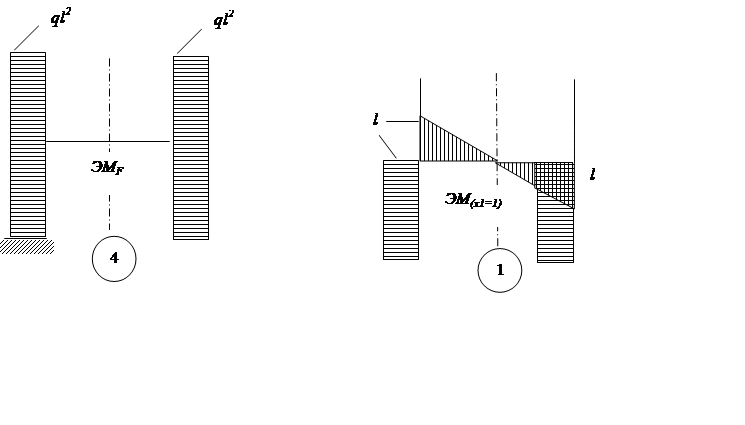 |
|||||||
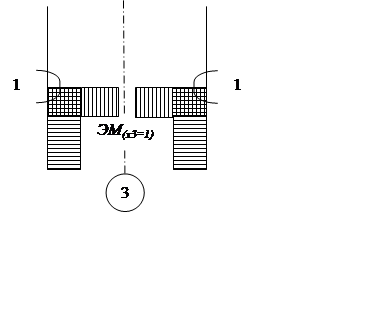 |
|||||||
 |
|||||||
 |
|||||||
х
 |
х
 |
х
 |
х
 |
х
 |
х
 |
х
 |
х
 |
х
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||
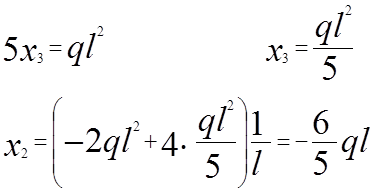
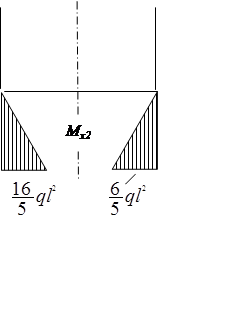
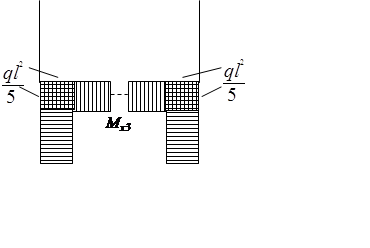
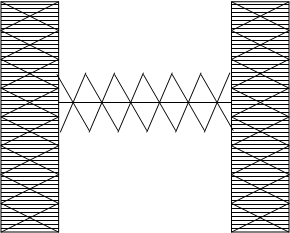
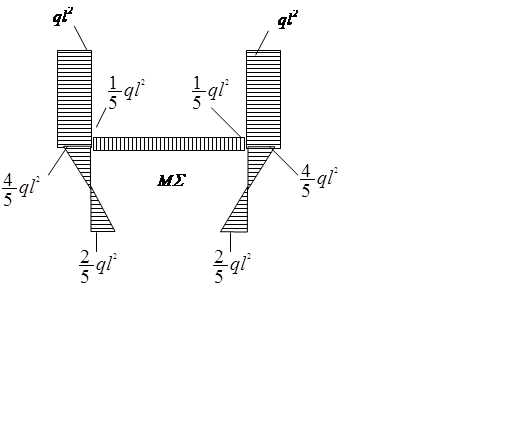
Симметричные факторы являются зеркальным отображением друг друга относительно оси симметрии.
Кососимметричные факторы тоже являются зеркальным отображением друг друга, но с противоположным знаком.
В симметричной раме при симметричной нагрузке, кососимметричные факторы обращаются в ноль.
В симметричной раме при кососимметричной нагрузке обращаются в ноль симметричные факторы.
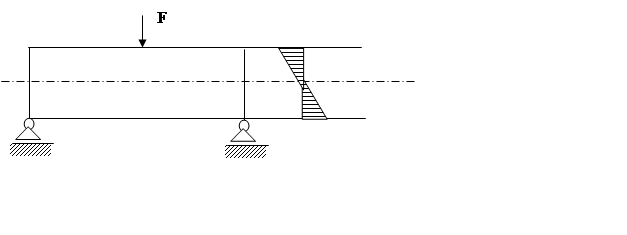 |
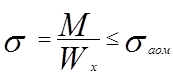
Предельное состояние наступит тогда, когда система перестанет воспринимать все возрастающую нагрузку или когда изменение геометрических размеров системы таковы, что она перестает выполнять свое назначение.
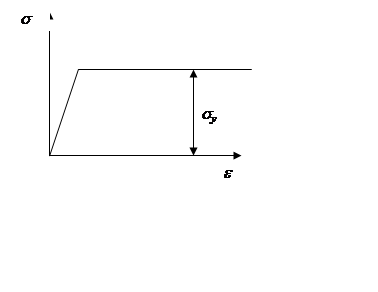
Под расчетом по методу предельной нагрузки понимается такой расчет, когда полученная диаграмма такого вида:
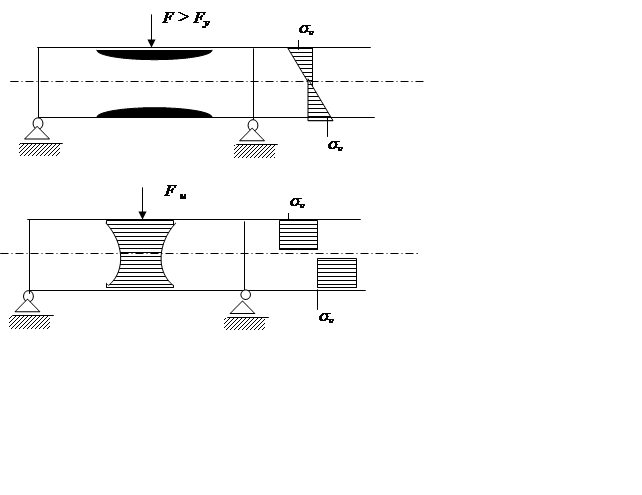
Состояние сечения, при котором напряжение на всей высоте сечения равно пределу текучести, называется пластическим шарниром, а нагрузка, при которой это происходит – пластической нагрузкой.
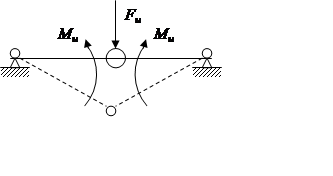
Свойства пластического шарнира:
1) действует в одну сторону;
2) при снятии нагрузки он закрывается (перестает быть шарниром);
3) имеет предельный момент.
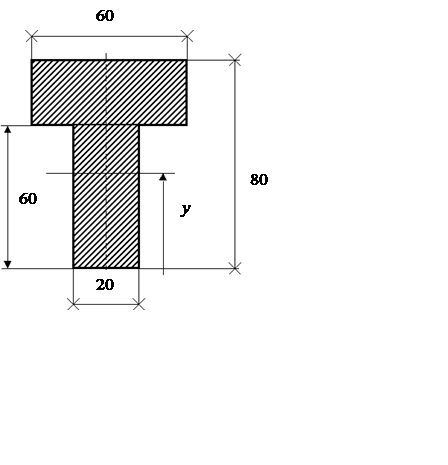
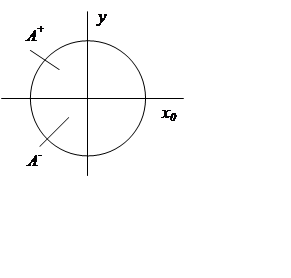 А+,
А- - площадь растянутой (сжатой) части сечения.
А+,
А- - площадь растянутой (сжатой) части сечения.
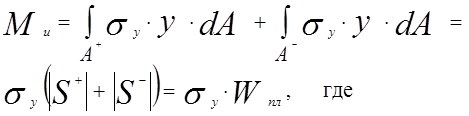
Wпл – пластический момент сопротивления;
x0 – находится из равенства А+ = А-
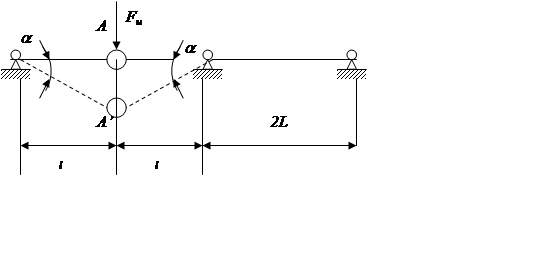
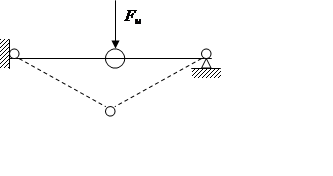 Балка перейдет в предельное
состояние тогда, когда в ней образуется столько пластических шарниров, что она
станет кинематически изменяема.
Балка перейдет в предельное
состояние тогда, когда в ней образуется столько пластических шарниров, что она
станет кинематически изменяема.
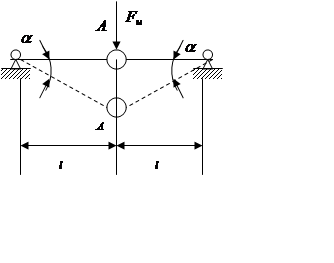
Суммарная работа всех внешних и внутренних сил на возможном перемещении равна нулю.
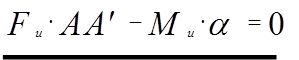 |
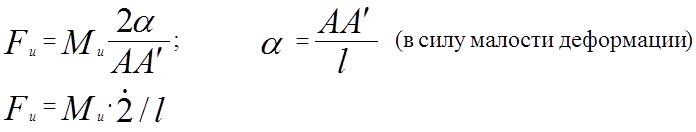 |
 |
|||
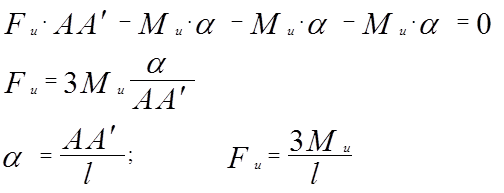
Истинному переходу балки в предельное состояние соответствует состояние с наименьшей предельной нагрузкой.
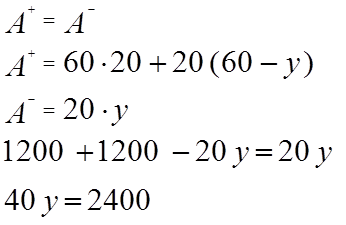
 |
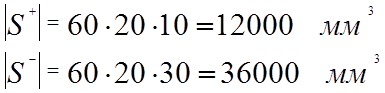
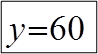 |
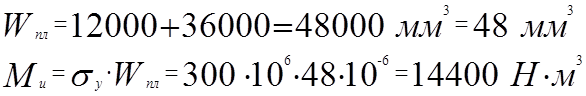 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.