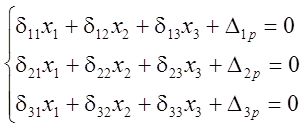
Полученная система уравнений носит название системы канонических уравнений метода сил. Для её решения необходимо построить эпюры изгибающих моментов от внешней нагрузки (грузовая эпюра) (рис. 12,в) и единичных усилий (Х1=1; Х2=1; Х3=1;) (рис. 12,г) и пользуясь методом Мора вычислить коэффициенты канонических уравнений (если возможно воспользоваться способом Верещагина)
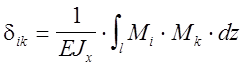 или
или 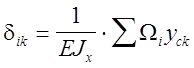
|
|
![]()
![]()
|
а |
|
б |
|
рис. 12 |
|
|
|
а |
|
г |
|
|
|
е |
|
д |
|
|
|
ж |
рис. 12 (продолжение)
В рассматриваемом примере:
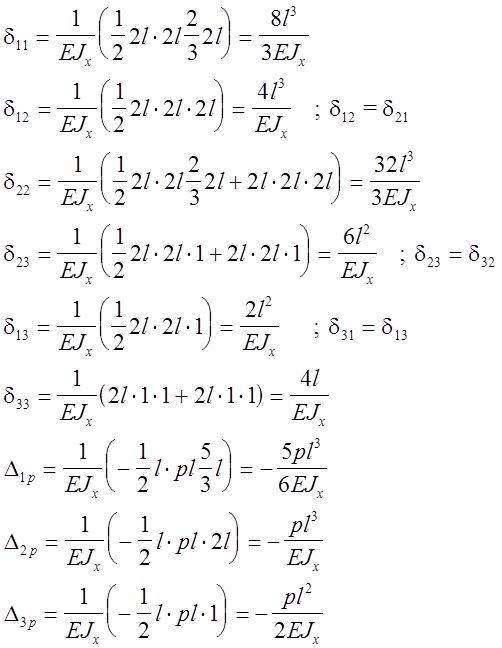
При определении коэффициентов необходимо помнить следующее:
I. Коэффициенты, имеющие двойные одинаковые индексы (d11; d22; d33; dii; и т.д.), называются главными. Они вычисляются умножением эпюр от единичных нагрузок самих на себя. Эти коэффициенты всегда положительны.
II. Коэффициенты имеющие разные индексы (d12; d31; d23; dij; и т.д.), называются побочными. Они вычисляются умножением эпюр от разных единичных сил друг на друга и могут быть положительными, отрицательными, нулевыми. Коэффициенты: d12; d31; d23; и т.д. - попарно равны между собой dij = dji(на основании теоремы о взаимности перемещений).
III. Грузовые коэффициенты (D1p; D2p; и т.д.) вычисляются умножением грузовой эпюры соответствующую единичную. При вычислении грузовых коэффициентов площади всегда берутся с криволинейной эпюры, а ордината под её центром тяжести - с линейной. Эти коэффициенты могут быть: положительными, отрицательными, нулевыми.
Найденные значения коэффициентов необходимо подставить в систему уравнений и решить последнюю.
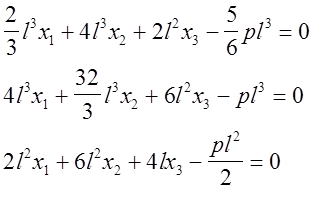
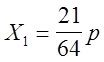
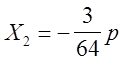
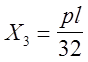
Задача считается решённой, если найдены значения всех неизвестных и построена суммарная эпюра изгибающих моментов. построение суммарной эпюры может быть выполнено двумя способами.
При первом способе построения основную систему нагружают внешними нагрузками и найденными значениями неизвестных усилий (рис. 12,д). Если в результате решения системы уравнений, оказалось, что какое-то из неизвестных имеет знак минус (в нашем случае Х2= -3р/64), то при нагружении этим усилием основной системы необходимо изменить его направление на противоположенное. Дальнейшее построение эпюры изгибающих моментов выполняется по общим правилам, т.е. для каждого участка рамы записываются уравнения изгибающих моментов и производятся соответствующие подсчёты.
Рама, представленная на рис. 12,д имеет три участка, для которых могут быть записаны следующие уравнения:
1.
участок (ВС): ![]()
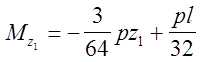
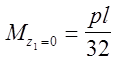
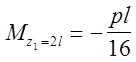
2. участок
(СD):
![]()
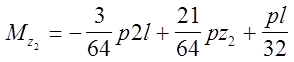
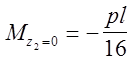
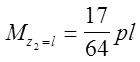
3. участок
(DА): ![]()
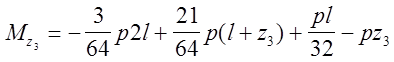
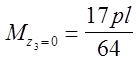
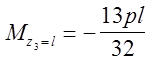
Суммарная эпюра изгибающих моментов представлена на рис. 12,е.
При другом способе построения, эпюра МS , построенных от действительных значений Х1;Х2 и т.д., найденных при решении системы уравнений, и грузовой эпюры. В нашем случае: эпюры от Х1;Х2;Х3; (рис. 12,ж) и эпюры от внешних нагрузок (рис. 12,в).
Суммирование производится по точкам.
Точка В
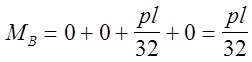
Точка С
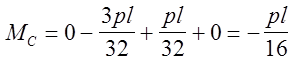
Точка D
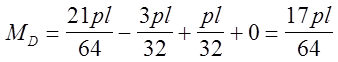
Точка A
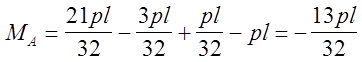
Найденные значения соответствуют вычисленным ранее при построении суммарной эпюры первым способом (рис. 12, е).
3.2.а.2. Проверка правильности полученного решения.
Известно, что перемещение по напровлению действия связи должно отсутствовать. Это условие и используется при проверке.
Для исследуемой рамы выбирают новую основную систему (рис. 13,а) и нагружают её единичной нагрузкой, действующей по направлению одной из отброшенных связей (рис. 13,б). От действия этой нагрузки строят единичную эпюру (рис. 13,в). Эту эпюру по правилу Верещагина перемножают с эпюрой М (рис. 12,е); результат перемножения должен дать 0.
В ряде случаев непосредственное вычисление площадей элементов суммарной эпюры и определение их центров тяжести бывает затруднительно.
|
|
рис. 13
Поэтому перемножение суммарной эпюры на единичную можно заменить перемножением составляющих суммарной эпюры (рис. 12,в,ж) на единичную (рис. 13,в) с последующим суммированием результатов.
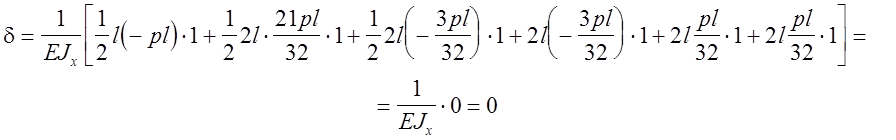 Угол поворота
сечения в точке А (рис. 12) оказался равным нулю, что соответствует
действительности, т.к. углы поворота защемлениях отсутствуют.
Угол поворота
сечения в точке А (рис. 12) оказался равным нулю, что соответствует
действительности, т.к. углы поворота защемлениях отсутствуют.
3.2.а.3. Пример расчёта статически неопределимых рам.
Пример I. Для рамы, изображённой на фиг. 14,а требуется раскрыть статическую неопределимость и построить суммарную эпюру изгибающих моментов. Моменты инерции стоек рамы и её горизонтального элемента (ригеля) различны и показаны на чертеже. Число неизвестных опорных реакций, рассматриваемой рамы, равно пяти, так что две из них являются «лишними».
Основная и эквивалентная системы, а так же эпюры изгибающих моментов от заданной нагрузки и от лишних неизвестных Х1 и Х2 = 1 показаны на фиг. 14,б,в,г,д,е.
Канонические уравнения метода сил имеют вид:
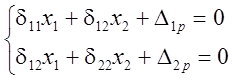
|
|
|
а |
|
б |
|
в |
|
г |
|
д |
|
е |
Фиг. 14
Коэффициенты этих уравнений вычислим по формуле Верещагина:
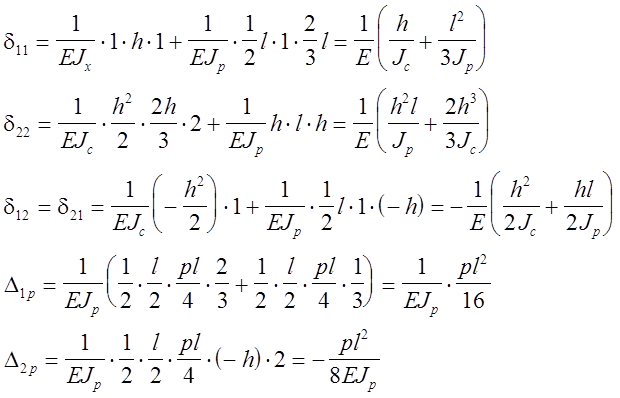
Подставим найденные значения коэффициентов в систему канонических уравнений и решим последнюю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.