Таким образом, вид канонического уравнения значительно упрощается:
![]()
По общему правилу определяем коэффициенты полученного уравнения:
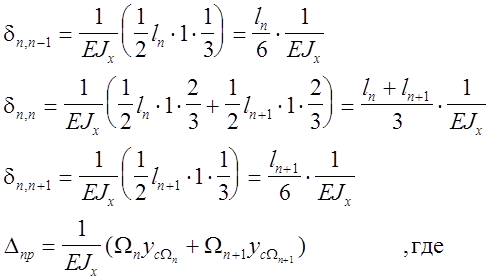
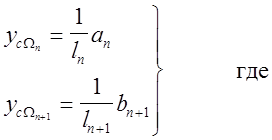
 - реакции на
опорах (n-1) и (n+1) от
момента Мn=1
- реакции на
опорах (n-1) и (n+1) от
момента Мn=1
![]() n - горизонтальная проекция отрезка, соединяющего правую
опору пролёта ln с центром тяжести
грузовой эпюры в этом пролёте,
n - горизонтальная проекция отрезка, соединяющего правую
опору пролёта ln с центром тяжести
грузовой эпюры в этом пролёте,
bn+1 - горизонтальная поекция отрезка, соединяющего правую опору пролёта ln+1 с центром тяжести грузовой эпюры в этом пролёте.
Выполнив все подстановки получаем:
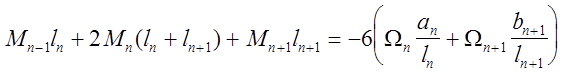
В уравнение входят три момента на трёх соседних опорах, поэтому оно носит название «уравнение трёх моментов».
3. 2. б. 5. Примеры решения задач с помощь уравнения трёх моментов.
Для балки, изображённой на рис. 26, а построить эпюру изгибающих моментов. При решении задачи придерживаемся следующего порядка:
1) Устанавливаем степень статической неопределимости; заданная система один раз статически неопределима.
2) Получаем основную, а затем эквивалентную системы (рис. 26,б). Для этого врезаем над опорами шарниры и прикладываем в них моменты.
3) Строим эпюры изгибающих моментов от внешних нагрузок, действующих в пролётах (рис. 26, в).
4) Записываем уравнение 3-х моментов применительно к рассматриваемой задаче.
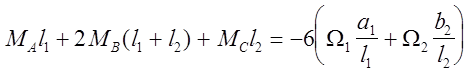
5) Анализируем уравнение и решение его.
|
|
Рис. 25
|
|
|
а |
Опоры А и С являются концевыми шарнирными опорами. Изгибающий момент (внутренний силовой фактор) над такими опорами равен нулю, если нет внешних нагрузочных моментов.
|
б |
Следовательно:
МА=МС=0
Согласно общим положениям правила Верещагина
|
в |
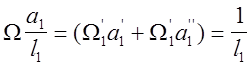 т. е.
т. е.
|
г |
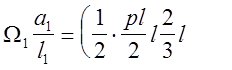
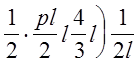
|
д |
|
е |
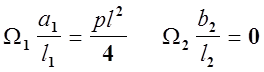
т. к. на втором пролёте нетт внешних нагрузок. Окачательно уравнение примет вид:
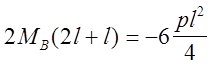
|
ж |
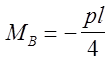
|
Рис. 26 |
6) Построение суммарной эпюры изгибающих моментов.
Суммарная эпюра изгибающих моментов может быть построена двумя способами: графическим суммированием, непосредственным построением. Использование графического суммирования более удобно, если грузовые эпюры линейны (как в нашем случае).
Порядок построения в этом случае следующий.
Сначала строим эпюры изгибающих моментов от найденного значения МВ на эпюру изгибающих моментов от внешних нагрузок (рис. 26, д). Перестраеваем -получаем окончательную суммарную эпюру (рис. 26, е).
при втором способе иостроения рассматриваются две
самостаятельные балки АВ и ВС. Балка АВ нагружена внешней
нагрузкой и момент МВ=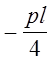 .
От их действия вычисляются опрные реакции и по общему правилу строится эпюра
изгибающих моментов (см. Рис. 26, ж). Аналогично решается балка ВС.
.
От их действия вычисляются опрные реакции и по общему правилу строится эпюра
изгибающих моментов (см. Рис. 26, ж). Аналогично решается балка ВС.
|
|
Пример 2.
|
а |
Раскрыть статическую неопределимость. Построить суммарную эпюруизгибающих моментов (рис. 27, а).
Для решения задачи вводим фиктивный пролёт СА и далее поступаем по общему правилу: врезаем над опорами шарниры, прикладываем в них моменты и нагружаем балки внешними нагрузками (рис. 27,б).
|
в |
Записываем уравнение трёх моментов:
![]()
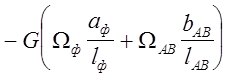
|
г |
Опора С является фиктивной опорой, поэтому момент на ней равен нулю: Mc=0
Пролёт СА является фиктивным пролётом в реальной балке он отсутствует, поэтому lCA=lф=0.
|
Рис. 27 |
Опора В разделяет пролёт lAB и консоль.
Момент возникающий над опорой, создаётся нагрузкой действующей на консоли.
Таким оброзом
Т. к. пролёт СА является фиктивным, то и
выражение 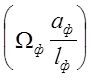 для него отсутствует, т. е.
для него отсутствует, т. е.
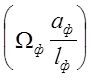 =0
=0
для определения величены 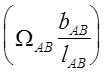 строим
эпюру изгибающих моментов от действия силы Р в пролёте АВ (рис.
27, в)
строим
эпюру изгибающих моментов от действия силы Р в пролёте АВ (рис.
27, в)
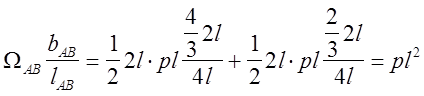
|
|
Окончательно получаем:
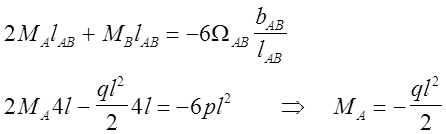
|
а |
Суммарную эпюры изгибающих моментов от внешней нагрузки (МР), нагрузки на консоли (МВ) и моментов в заделке (МА), получаем суммарную эпюру изгибающих моментов (рис. 27, г).
3. 2. б, 6. Использование свойств симметрии и косой симметрии при расчёте
статически неопределимых балок.
|
б |
Балка АВ, представлена на рис. 28, является симметричной как по конструкции, так и по нагружению. Она дважды статически неопределима, т. к. горизонтальные составляющие опрных реакций на опорах А и В равны нулю.
|
в |
Решение задачи значительно упрощается, если использовать свойство симметрии.
|
Рис. 28 |
Разрежим балку по оси симметрии и в месте разреза приложим внутренние силовые факторы Mx=X1 и Qy=X2 (N=X3, как уже говорилось ранее, равно 0)(рис.28,а).
Поперечная сила Qy(или Х2)согласно свойству симметрии, равна нулю.
Таким образом единственным неизвестным является изгибающий момен Мх=Х1. Далее решаем задачу по общему правилу (рис. 28, б).
|
|
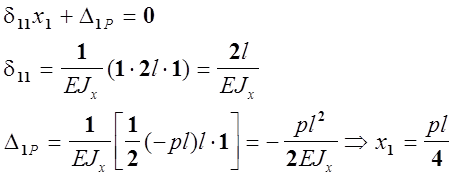
Суммарная эпюра изгибающих моментов представлена на рис. 28, в.
|
а |
Балка АВ, представленная на рис. 29, симметрична по конструкции, но кососеметрична по нагрузкам.
Она дважды статически неопределимая, т. к. горизонтальные составляющие опорных реакций равны нулю.
|
б |
Для упрощения решения используем свойство косой симметрии. Разрежем балку по оси симметрии и в месте разреза приложим неизвестные усилия Х1; Х2; Х3;
Х3=0
(из условия) ![]()
Х2=0 (из свойства косой симметрии.)
|
в |
Таким образом единственным неизвестным будет поперечная сила Х2 (рис.29,б).
Далее решаем задачу по общему правилу:
|
Рис. 29 |
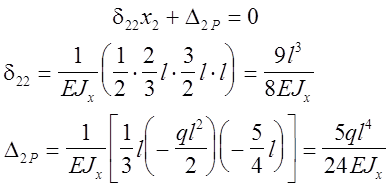
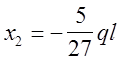
Суммарная эпюра изгибающих моментов представлена на рис,29,в.
Литература.
Феодосьев В. И. Сопративление материалов
Москва, Наука, 1979 год, число стр.-560
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.