|
|
Тогда основная система (см. Раздел 2.2) принимает вид
консольной балки (рис. 21, б), а эквивалентная - этой же балки нагруженной
внешним усилием Р и неизвестной опорой Х1 (рис. 21,
в). Система, представленная на рис. 21, в будет эквивалентна заданой, если сила
Х1 будет подобрана так, что вертикальное перемещение
на опоре В будет отсутствовать. Это условие может быть записано в виде
канонического уравнения метода сил: 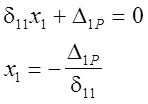 Как и в
предыдущих примерах, коэффициенты канонического уравнения определяем по способу
Верещагина, построив предварительно эпюру изгибающих моментов от внешней
нагрузки (рис. 21, г) и Х1=1 (рис. 21, д)
Как и в
предыдущих примерах, коэффициенты канонического уравнения определяем по способу
Верещагина, построив предварительно эпюру изгибающих моментов от внешней
нагрузки (рис. 21, г) и Х1=1 (рис. 21, д) 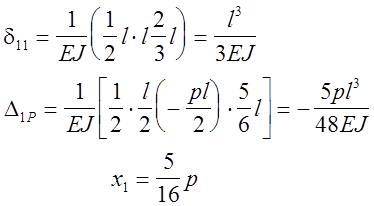
|
Рис. 21 |
По одному из рассмотренных ранее (стр. 13) способов, строим суммарную эпюру изгибающих моментов (суммарная эпюра изгибающих моментов представлена на рис. 21, е).
3.2.б,2. Проверка правельности решения.
|
|
|
а |
Известно, что угол поворота сечения в заделке равен 0. Определим этот угол поворота в сечении А балки АВ изображённой на рис. 21. Для этого выберем новую основную систему и нагрузим её единичным усилием, действубщим по направлению отброшенной связи (рис. 22, а).
|
б |
|
Рис. 22 |
Эпюра изгибающих моментов от этого усилия представлена
на рис. 22, б. Перемножим по правилу верещагина эпюры, представленные на рис.
21, е и 22, б. Использовав расслоение: 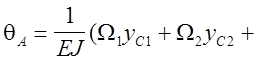
![]() W1; W2; W3
- площади элементов расслоений эпюры. уС1; уС2;
уС3 - ординаты взятые под центрами тяжести этих площадей.
W1; W2; W3
- площади элементов расслоений эпюры. уС1; уС2;
уС3 - ординаты взятые под центрами тяжести этих площадей.
|
|
|
|
. Угол поворота в заделке равен 0 - задача решена верно.
|
а |
3.2.б,3. Примера расчёта статически неопределимых балок.
Пример 1.
|
в |
|
б |
Дана один раз статически неопределимая балка (рис. 23, а). Необходимо раскрыть статическую неопределимость эпюру изгибающих моментов.
|
г |
Считаем среднюю опору «лишней» и заменяем её действие силой Х1.
|
Рис. 23 |
|
д |
Система, эквивалентная заданной, представленной на рис. 23,б. Составим каноническое уравнение метода сил, смысл которого сводится к следующему: вертикальное перемещение в точке В эквивалентной системы от совместного действия сил Р и Х должно быть равно нулю, т. к. В исходной схеме вертикальное перемещение на опоре В отсутствует
![]()
Строим эпюры изгибающих моментов от сил Р (рис. 23, в) и силы = 1 (рис.23,г); определяем коэффициенты канонического уравнения.
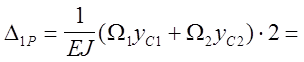
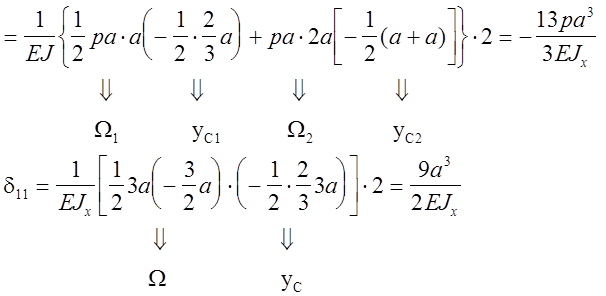
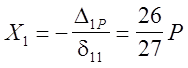
Строим суммарную эпюру изгибающих моментов.
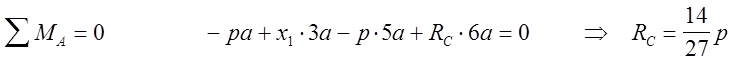
В силу симметрии RA=RC=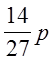
I. участок:
0
< Z1 < ![]()
![]()

II. участок:
![]()
![]()

(т.к. балка симметрична, то два других участка не рассматриваются).
Суммарная эпюра изгибающих моментов представлена на рис. 23, д.
Пример 2.
Дана один раз статически не определимая балка (рис. 24, а). Раскрыть статическую неопределимость и построить эпюру изгибающих моментов, если жёсткость балки EJx= Const.
Считаем правую опору «лишней» и заменяем её действие силой Х1. Система, эквивалентная заданной, представлена на рис. 24, б.
Составим каноническое уравнение метода сил.
![]()
Строим эпюры изгибающих моментов от внешней нагрузки и силы =1 (рис. 24,в); определяем коэффициенты канонического уравнения.
|
|
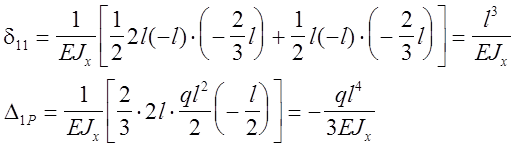
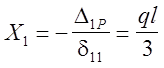
|
а |
Строим суммарную эпюру поперечных сил и изгибающих моментов (используем схему Рис. 24, г.).
|
б |
![]()
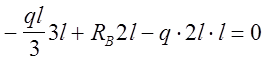
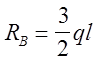
![]()
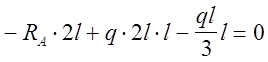
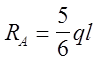
Строим эпюру поперечных сил (рис. 24, д)
I.
участок: 0 < Z1 < 2l ![]()
|
г |
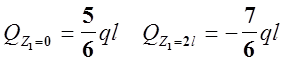
II. участок:
0
< Z2 < l
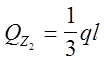
|
д |
Строим эпюру изгибающих моментов
(рис. 24, е).
I. участок:
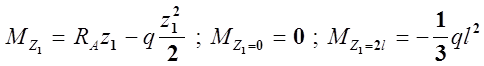
|
Рис. 24 |
I. участок:
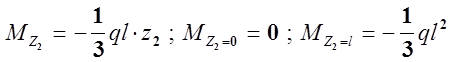
Определяем Mmax : Mzi=Mmax , если Qzi=0, т. к. Q =![]()
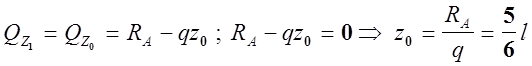
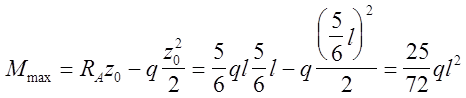
3. 2. б. 4. Частный случай метода сил - уравнение трёх моментов.
Как уже говорилось ранее (стр. 6), при выборе основной системы для балки за «лишние» неизвестные можно принять не только реакции «лишних» опор, но и надопорные изгибающие моменты (рис. 10).
Рассмотрим многопролётную статически неопределимую балку рис. 25, имеющую К опор.
Для упращения анализа считаем жёсткость по всей длине балки постоянной EJx= Const.
Чтобы построить суммарную эпюру изгибающих моментов, необходимо раскрыть статическую неопределимость. В качестве «лишних» неизвестных принимаем надопорные моменты. Тогда основной системой будет ряд самрстаятельных статически определимых балок, нагруженных внешними нагрузками и неизвестными надопорными моментами.
Рассмотрим перемещение на опоре n. Им будет угол поворота надопорного сечения. Угол поворота сечения над опорой n балки длиной ln относительно сечения над опорой n балки длиной ln+1 должен отсутствовать, т. е. равен нулю.
В противном случае нарушается условие неразрывности, т. к. Конец одного пролёта является началом следующего пролёта.
Каноническое уравнение для опоры может быть записано в следующем виде:
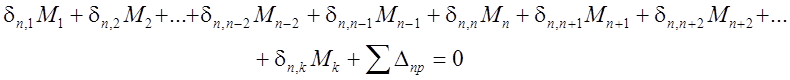
Определим коэффициенты этого уравнения, для чего строим эпюры изгибающих моментов от внешних нагрузок и моментов М1, М2,……,Мк, равна 1.
Из анализа эти эпюру (рис. 25) следует, что все единичные коэффициенты от: dn,1 до dn,n-2 и от dn,n+2 до dn,k - равны нулю; грузовой коэффициент будет состоять только из двух слагаемых: D’n,p на участке ln и D’’ n,p на участке ln+1 - остальные обращаются в 0. (Dn,p= D’n,p+ D’’n,p).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.