Расчёт статически неопределимых систем (рам и балок): Методическое пособие, страница 4

Если принять:

       

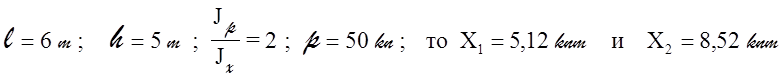
После этого одним из выше указанных методов строим суммарную эпюру изгибающих моментов (фиг. 15).

Фиг. 15

Пример II. Для рамы изображённой на фиг.16,а, требуется раскрыть статическую неопределимость и построить суммарную эпюру изгибающих моментов.

Фиг. 16

Число неизвестных опорных реакций рассматриваемой рамы равно четырём, так что одна из них является лишней.

Основная и эквивалентная системы, эпюры от заданных нагрузок и эпюра от    Х₁ =1 показаны на фиг.16,б,в,г,д,е.

Каноническое уравнение метода сил имеет вид:

           или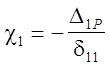            

Коэффициенты будем определять по правилу Верещагина.

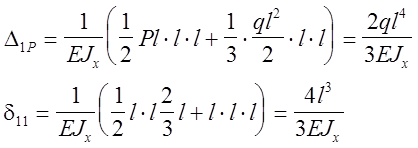
Подставим найденые коэффициенты в каноническое уравнение получим :

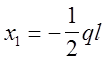
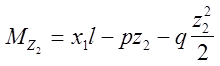
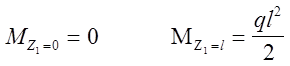
Строим сумарную эпюру изгибающих моментов (фиг. 17,а,б)

                                                                                      

                                                                                   

                               

Фиг. 17

Пример 3. Дана статически неопределимая рама симметричной конструкции с симметричным нагружением (рис.18,а).

Необходимо построить суммарную эпюру изгибающих моментов проверить правельность решения.

Эта рама три раза статически неопределима.

В качестве лишних неизвестных выступают внутренние силовые факторы на оси симмтрии (рис.18,б    и рис.18,в):

изгибающий момент X₁,

пордольная сила        X₂,

поперечная сила        X₃.

Относительно оси симметрии X₁ и Х₂ являются симметричными нагрузками;     Х ₃ - кососимметричной нагрузкой.

Составим систему канонических уравнений

     

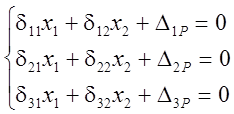
и построим соответствующие эпюры изгибающих моментов отединичных сил (рис.18, г) и внешних нагрузок (рис.18, д).

При подсчётах получается, что .

Тогда:

Рис. 18

 

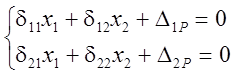
Таким образом, за счёт рационального выбора основной системы, система канонических уравнений значительно упростилась. Это позваляет сформулировать следующие правило:

если система симметрична и для её расчёта выбрана симметричная основная система, то при действии симметричной нагрузки кососимметричные неизвестные обращаются в нуль.

                   

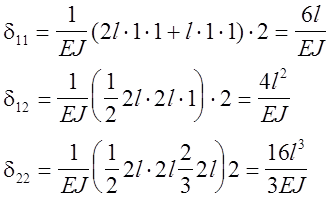
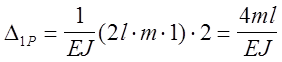
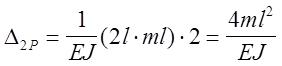
и

              

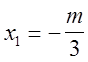
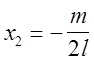
Перестраиваем эпюры от Х₁ и Х₂ (рис.18, е) и строим суммарную эпюру (рис.18,ж).

Проверяем правильность полученного решения.

Если задача решена верно, то угол поворота на опоре В должен отсутствовать.

Выбераем новую основную систему для чего отбрасываем на опоре В три «лишних» связи: горизонтальную и вертикальную составляющие реакции и реактивный момент (рис.18, з). Заменяем действие одной из отброшенных связей (в нашем примере - момента) единичной нагрузкой (рис.18, и) и стороим эпюру изгибающих моментов от действия этой нагрузки (рис.18, к).

Определяем угол поворота на опоре В

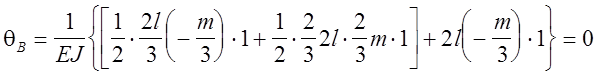
следовательно задача решена верно.

Прмер 4.

Дана статически неопределимая рама симетричной конструкции с кососимметричным нагружением (рис.19, а). Построить суммарную эпюру изгибающих моментов.

Эта рама, как и в предыдущем случае, три раза статически неопределима, т. е. Для решения задачи необходимо записать систему из трёх уравнений с тремя неизвестными. (См. Предыдущий пример).

Коэффициенты при неизвестных в этих уравнениях определяются по общему правилу. Эпюры изгибающих моментов от сил Х₁ = 1; Х₂=1; Х₃=1 такие же, как в примере 3 (рис.18, г), а грузовая эпюра представлена на рис. 19, д.

При определение коэффициентов получается, что

 

Тогда система канонических уравнений примет вид:

Рис. 19

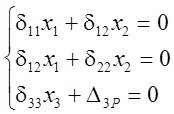
Первые два уравнения имеют только нулевое решение:

Х₁=0 и Х₂=0; таким образом, остаётся одно уравнение с одним неизвестным:

Итак, если система симметрична и для её расчёт выбрана симмтричная основная симметричные неизвестные обращаются в нуль.

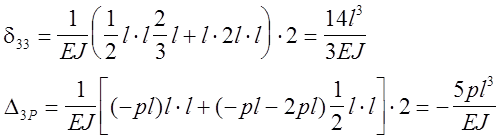
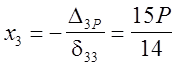
Строим суммарную эпюру изгибающих моментов (рис. 19, е).

Пример 5.

Дана статически неопределимая рама симметричной конструкции с произвольными нагружением (рис. 20, а).

Построить эпюру изгибающих моментов, возникабщих в элементах рамы.

Эта рама трижды статически неопределима. Данная задача имеет два варианта решения. По первому варианту исходная задача может быть разбита на две более простых (рис. 20, б), решения которых будут анфлогичны приведённым в предыдущих примерах (3 и 4). Схема решения по второму варианту приведена на рис. 20,в,г.

В этом случае система трёх уравнений с тремя неизвестными имеет ряд нулевых коэффициентов (d₂₁=d₁₂=0,  d₁₃=d₃₁=0) и значительно упрощается:

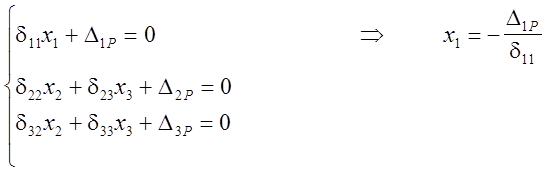
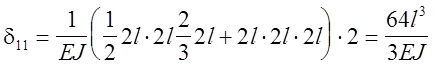
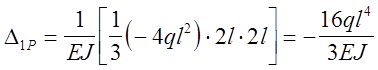
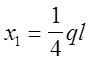
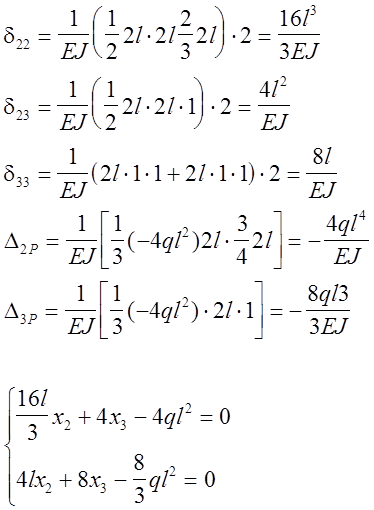
Решая систему уравнений получаем:

Проверка подтверждает правильность полученного решения.

Суммарная эпюра изгибающих моментов представлена на рис. 20, д.

3.2, б. Статически неопределимые балки.

3.2, б, 1. Метод сил.

На рис. 21,а изображена балка один раз статическм неопределимая. Для этой балки за «лишнее» неизвестное удобнее всего принять реакцию, которая возникает на опоре В при действии внешней нагрузки Р.