Расчёт статически неопределимых систем (рам и балок): Методическое пособие, страница 2

Наиболее рациональным будет вариант «в» (рис.3), при котором часть неизвестных окажутся равными нулю. Более подробно об этом будет сказано при разборе примеров.

2.2 Основная и эквивалентная системы для балок.

При выборе основной системы для балок возможны два подхода. В одних случаях за «лишние» неизвестные целесообразно принимать вертикальные составляющие опорных реакций (рис.9,а). Тогда основной системой будет статически определимая балка значительной длины (рис.9,б), а эквивалентной - эта же балка, нагруженная внешними силами и специально подобранными усилиями  X , обеспечивающими отсутствие вертикальных смещений на опорах В и С (рис.9,в).

В других случаях в качестве «лишних» неизвестных целесообразно взять надопорные изгибающие моменты (рис.10).

В

В этом случае основной системой будет ряд последовательно стоящих статически определимых балок, а эквивалентной - эти же балки нагруженные внешними нагрузками и надопорными моментами, выполняющими функции неизвестных усилий. Величина моментов должна быть подобрана так, чтобы не было разрыва сплошности балки и углы поворота концевых сечений одной балки относительно другой отсутствовали.

3. СОСТАВЛЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ МЕТОДА СИЛ

 И ИХ РЕШЕНИЕ.

3.1. Основные положения сопротивления материалов,

        используемые при расчёте рам и балок.

3.1, а. Принцип неизменяемости начальных размеров.

Рассматриваемые конструкции рам и балок являются достаточно жёсткими, а материал, из которого они изготовлены, достаточно упругим. Нагрузки, действующие на конструкцию, не вызывают в её элементах пластических деформаций. Все деформации происходят в пределах упругости, перемещения (как линейные, так и угловые) настолько малы, что форма и размеры конструкции практически не изменяются. Это позволяет использовать для расчётов постоянную схему, сохраняющую свою первоначальную форму и размеры. Такой подход открывает широкие возможности для применения принципа независимости действия сил.

3.1, б. Принцип независимости и сложения действия сил.

Так как конструкция работает в пределах упругости, то конечный результат силового воздействия не зависит от порядка приложения сил.

Применительно к случаю статически неопределимых рам и балок это означает следующее: если на раму (балка) действует группа внешних сил, то внутренние усилия, в интересующем сечении, или смещения, в интересующем направлении, могут быть вычеслины от каждой силы отдельно, а результаты просуммированы.

Так, например, при определении суммарного изгибающего момента в сечении балки (рис.11, а) можно построить отдельно эпюры от «m» и «P», а результаты сложить (рис.11, б). В случае необходимости можно поступить и наоборот: «расслоить» сложную эпюру (на участке ВС) на более простые (рис.11, в).

Всякая внешняя нагрузка может быть представлена в виде произведения  I*P  или  I*m, где I имеет точку приложения и направление действия, а сомножитель Р определяет абсолютное значение силы (или момента). Аналогично может быть представлено любое известное или неизвестное усилие Х, т.е. Х=1*Х . Приём расслоения эпюр используется и при определении перемещений, возникающих вследствие действия внешних сил. Перемещения принято обозначать  D_ikи d_ik, где первый индекс (i) обозначает точку и направление перемещения, а второй (k) указывает на силу, послужившую причиной перемещения. Так для схемы нагружения, представленной на рис.11, перемещение в точке А по направлению силы «Р» будем считать первым направлением, а саму силу Р - первой силой; момент «m», приложенный в точке В - второй силой.

 Тогда перемещение (прогиб) в точке А будет:

                  или                  

 где d₁₁ - перемещение по направлению первой силы действия первой силы, равной 1,

       d₁₂ - перемещение по направлению первой силы от действия второй силы, равной 1.

                        

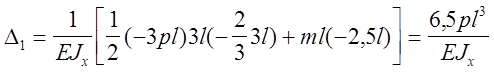
                      или

                      

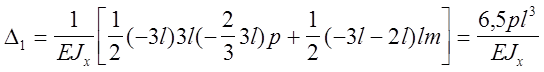
Соответственно, угол поворота сечения в точке В будет равен:                           или                            

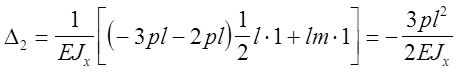
                       или

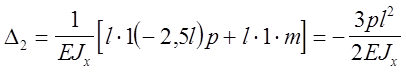
3.1, в. Взаимность перемещений.

Перемещение точки приложения первой силы по направлению первой силы, вызванное второй силой, равно перемещению точки приложения второй силой, если силы между собой равны, т.е.

d₁₂=d₂₁

Так, в рассмотренном выше примере,

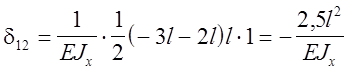                     ,   а

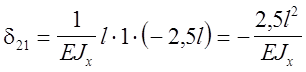            ,  т.е.     d₁₂=d₂₁

Таким образом, если найден коэффициент d₁₂, то нет обходимости вычислять коэффициент d₂₁, и при решении задач можно сократить объём вычислений.

3.2. Канонические уравнения метода сил.

Используя всё выше изложенное, можно приступить к составлению уравнений, описывающих особенности работы статически неопределимых рам и балок.

3.2,а. Статически неопределимые рамы.

3.2,а.I. Подробный разбор раскрытия статической неопределимости у рам.

На рис. 12,а изображена плоская статически неопределимая рама с защемлёнными концами.

Эта рама трижды статически неопределима. Наиболее рациональным вариантом эквивалентной системы будет вариант, приведенный на рис. 12,б. Заданная конструкция рамы предполагает, что перемещения в точке В (защемлены) по всем трём направлениям (1,2,3) отсутствуют, т.е. D₁=0; D₂=0; D₃=0.

В развёрнутом виде это может быть записано следующим образом: