6. Статистически неопределимые системы
6.1. Основные понятия и определения
Статистически неопределенной является такая механическая система, в которой число неизвестных превышает число статистических уравнений. Порядок статистической неопределимости равен разности числу неизвестных реакций связи число уравнений статистических равновесия.
n = N1 – N2 (6.1)
Для раскрытия статистической неопределимости мы должны использовать уравнения совместимости деформаций. Подавляющая часть современных конструкций зданий, сооружений, машин и т.д. являются статистически неопределимыми.
6.2. Статистически неопределимые системы, работающие
на растяжение и сжатие
Целью использования статистически неопределимых систем в технике, является для увеличения прочности и жесткости.
6.2.1. Статически неопределимая система, у которой все связи сходятся в одной точке.
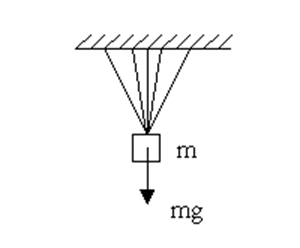
Рис. 6.1. Статически неопределимой системы, у которой
все связи сходятся в одной точке.
n = 3 – 2 = 1
Рассмотрим условия статистического равновесия. Используем метод сечения.
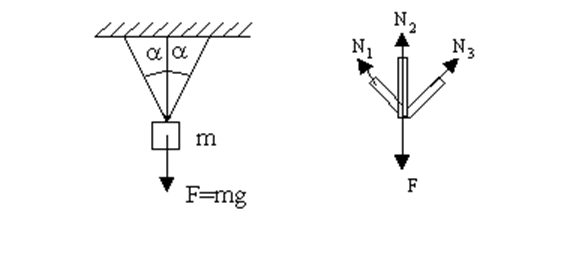
Рис. 6.2. Схема статистического равновесия
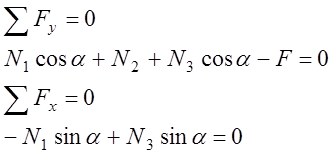
![]() (6.2)
(6.2)
После преобразований можно записать
![]() (6.3)
(6.3)
Рассмотрим условия совместности деформаций
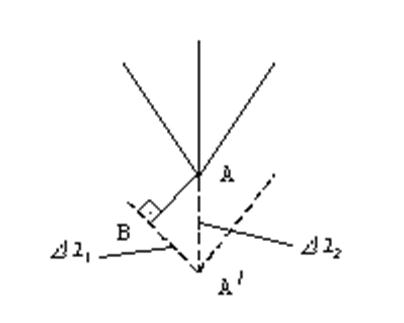
Рис. 6.3. План перемещений
В прямоугольном треугольнике ![]()
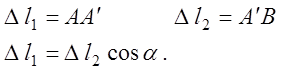
Выражая удлинения через продольные силы, получим
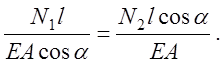
После преобразований уравнение совместности деформаций примет следующий вид
![]() (6.4)
(6.4)
Три
уравнения (6.2)-(6.4) образуют систему неоднородных линейных алгебраических
уравнений относительно ![]() .
.
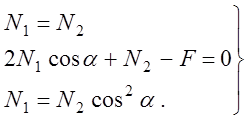 . (6.5)
. (6.5)
После некоторых преобразований получим
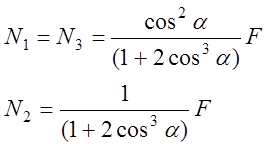 .
.
6.2.2. Статически неопределимые системы с параллельными связями
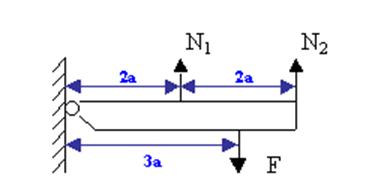
Рис. 6.5. Статически неопределимая система с параллельными связями
Для определения степени статической неопределимости можно воспользоваться тремя уравнениями равновесия для плоской системы сил
n1 = 4-3=1
или использовать одно условие
равновесия в моментах относительно точки ![]()
n2 =2-1=1.
Наиболее простое решение имеет место во втором случае.
Рассмотрим условия статистического равновесия. Используем метод сечения и рассечем стержни 1 и 2,
заменив действие отброшенной части продольными силами ![]() .
.
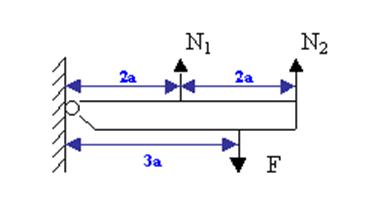
Рис. 6.6. Схема статистического равновесия
![]() ,
,
![]() . (6.6)
. (6.6)
Рассмотрим условия совместности деформаций
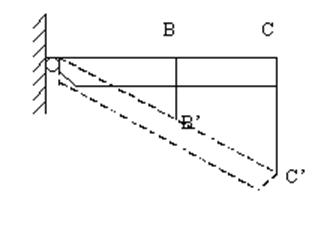
Рис. 6.7. План перемещений
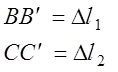
из подобия треугольников ∆ABB’ и ∆ACC’ можно получить условие совместности деформаций в виде
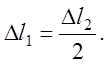
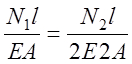 . (6.7)
. (6.7)
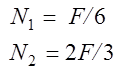
Для проверки используем уравнение статического равновесия в моментах относительно точки А:
![]() .
.
6.2.3. Стержни, жестко заделанные на границах
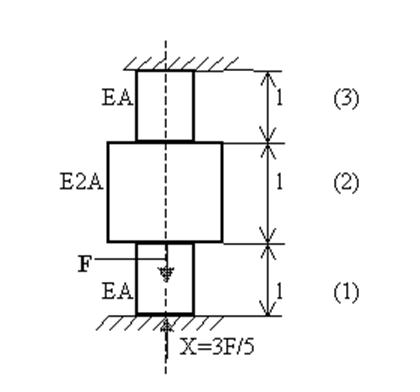
Рис.6.8. Стержень, жестко заделанный на границах
1. Вычисляем степень статистической неопределимости:
n= 2-1 =1
2. Отбросим лишнюю связь. Прикладываем неизвестную реакцию X. Если предположить, что X нам известно, то тогда данная система полностью эквивалентна исходной статически неопределимой системе, будем называть эквивалентной системой.
3. Перемещение в направление отброшенной связи должно быть равно 0. Это и есть уравнение совместности деформации.
 (6.8)
(6.8)
4. Выразим через X продольные силы для каждого участка.
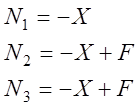
1. Используем выражения для продольных сил при вычислении удлинений стержней
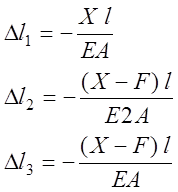
2. После подстановки этих выражений в зависимость (6.8) можно определить реакцию Х
![]()
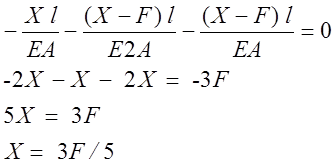
Следующие этапы решения задачи не чем не отличаются от расчетов статистически определимых систем, так как X=3F/5 можно считать внешней нагрузкой.
Для последнего примера произведем дополнительно
учет нагрева второго стержня на ![]() ○. На
участке (2) происходит удлинение, как за счет упругих деформаций, так и за счет
температурного расширения.
○. На
участке (2) происходит удлинение, как за счет упругих деформаций, так и за счет
температурного расширения.
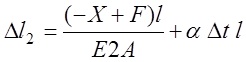
где
aсталь =125*10-4 1/○K
aалюминий=240*10-4 1/○K
С учетом отмеченных особенностей уравнение совместности деформаций (6.8) может быть записано в следующем виде
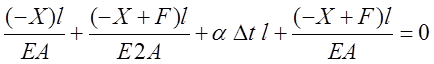
Статистические неопределимые системы с зазором и натягом. По технологическим или конструктивным причинам в технике используются зазоры и натяги. С учетом этого уравнение совместности деформаций (6.8) может быть записано в следующем виде
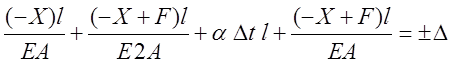
где ![]() - величина зазора (знак
положительный) или натяга (знак отрицательный).
- величина зазора (знак
положительный) или натяга (знак отрицательный).
Аналогичной зависимостью могут быть записаны и для двух первых примеров.
6.3. Статистически неопределимые задачи на кручение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.