Статистически неопределимые системы (работающие на растяжение и сжатие, на кручение, на изгиб), страница 2

Применение статически неопределимых систем, работающих на кручение, позволяет повысить прочность и конструктивную надежность целого ряда технических систем. Одним из примеров практического использования таких систем является планетарный редуктор, позволяющий при малых габаритах передавать значительную мощность при большом передаточном отношении. При кручении в поперечном сечении действует только один внутренний силовой фактор – крутящий момент, что делает рассматриваемые задачи очень близкими аналогичным задачам на растяжение и сжатие (рис. 6.9.)

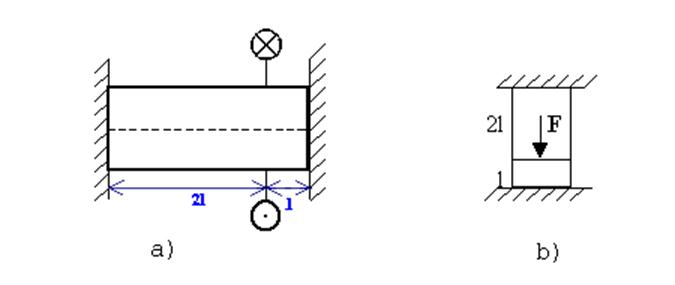
Рис. 6.9. Статически неопределимые стержни, работающие на кручение (а)
 или на растяжение и сжатие (b)

1.  Вычисляем степень статистической неопределимости:

n= 2-1 =1

2. Отбросим одну из связей и заменим ее действие крутящим моментом  (рис.6.10).

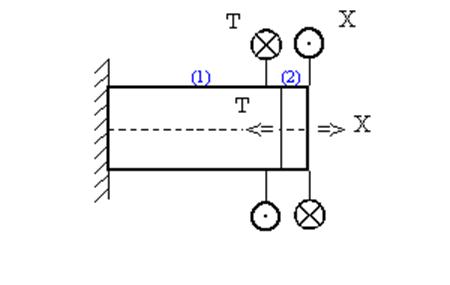
Рис.6.10. Эквивалентная система в статически неопределимых
задачах на кручение

3. Перемещение в направление отброшенной связи должно быть равно 0. Это и есть уравнение совместности деформации.

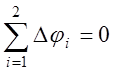                                                                                                      (6.9)

4. Выразим через X продольные силы для каждого участка.

 

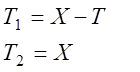
4.  Используем выражения для крутящих моментов при вычислении углов закручивания участков стержня

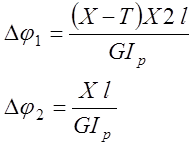
5.  После подстановки этих выражений в зависимость (6.9) можно определить реакцию Х

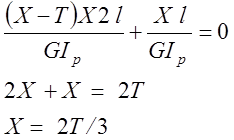
Следующие этапы решения задачи не чем не отличаются от расчетов статистически определимых систем, так как X=2Т/3 можно считать внешней нагрузкой. Суммарная эпюра крутящих моментов показана на рис. 6.11.

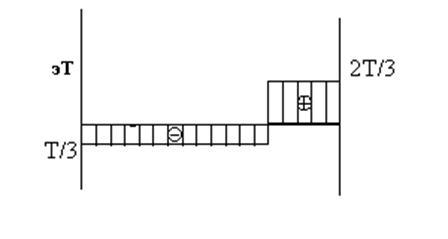
          Рис. Эпюра крутящих моментов для статически неопределимой балки

          Порядок дальнейшего решения задач прочности и жесткости при кручении практически не отличается от статически определимых задач, изложенных в разделе 4.

6.4. Статистически неопределимые задачи на изгиб

В природе и в технике широко используются статистически неопределимые балки и рамы, работающие на изгиб.

1.  Определяем степень статической неопределимости системы, работающей на изгиб

     n=N₁- N₂ или n=4-3=1

2.  Формируем основную систему. Основная система может быть образована из исходной системы, путем отбрасывания “лишних” связей. Число таких лишних связей равно степени статической неопределимости системы . Может быть отброшена любая связь. В рассматриваемом случае отбросим шарнирно подвижную опору  и введем неизвестную реакцию этой ”лишней” связи  (рис. 6.12).

3.   Для получения эквивалентной системы к основной системе прикладываем все внешние нагрузки и неизвестную реакцию связи X. Эквивалентно системе это основная система, которая приложена к внешней нагрузке и к реакции связи.  Эквивалентная система тождественна исходной системе, после вычисления X.

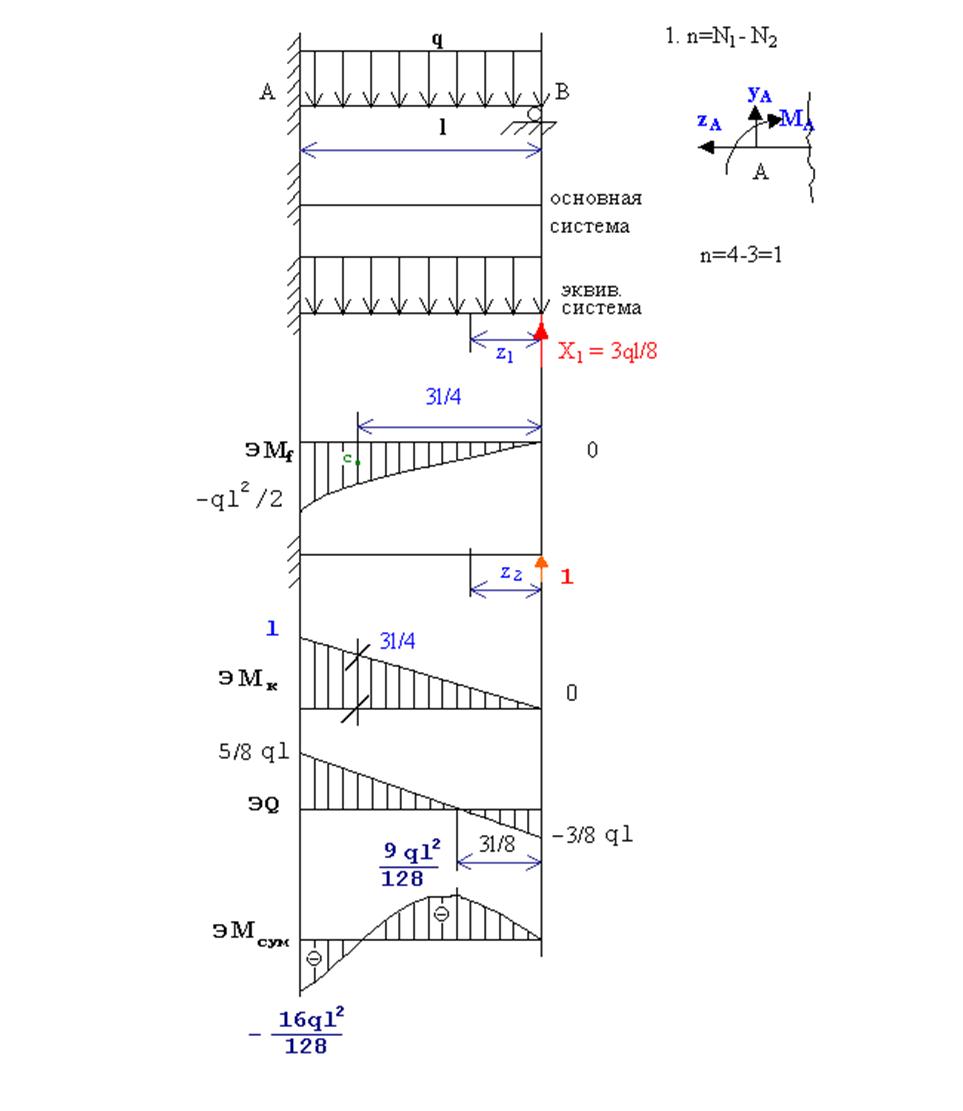
Рис. 6.12. Схема статически неопределимой балки,
грузовая, вспомогательная и суммарная эпюры

4.  Уравнение совместности деформаций в рассматриваемом примере требует, чтобы прогиб в точке  был равен нулю . В терминах перемещения это выглядит следующим образом

.                                                                                     (6.10)

где       – перемещение в точке  под действием единичной силы;

X     – неизвестная реакция отброшенной связи;

 – перемещение в точке  под действием внешних нагрузок.

          Воспользуемся способом Верещагина для вычисления коэффициентов  при построенных грузовой и вспомогательной эпюрах

           

                 

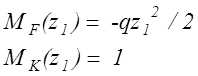
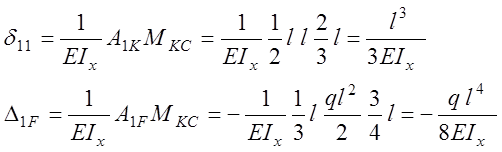
После подстановки этих коэффициентов в уравнение совместности деформаций находим реакцию

Дальнейший порядок вычислений точно такой же, как и в статистически определимых задачах на изгиб. После предварительного определения координаты сечения стержня с экстремальным значением изгибающего момента

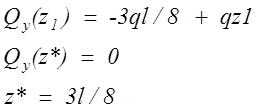
можно вычислить значения суммарного изгибающего момента в трех точках.

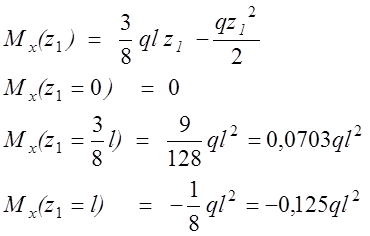
6.5. Метод сил.

Обобщим изложенный подход на  “лишних” связей. В методе сил каждое разрешающее уравнение по своей сути это есть условие совместности деформации, записанное для точек 1, 2, и т.д. (рис. 6.13).

Запишем это условие для первой точки. Сумма перемещений этой точки складывается из следующих составляющих:

     – перемещение точки 1 от внешних нагрузок;

 – перемещение от силы , действующей в направлении первой отброшенной связи;

 – перемещение от  и т. д.

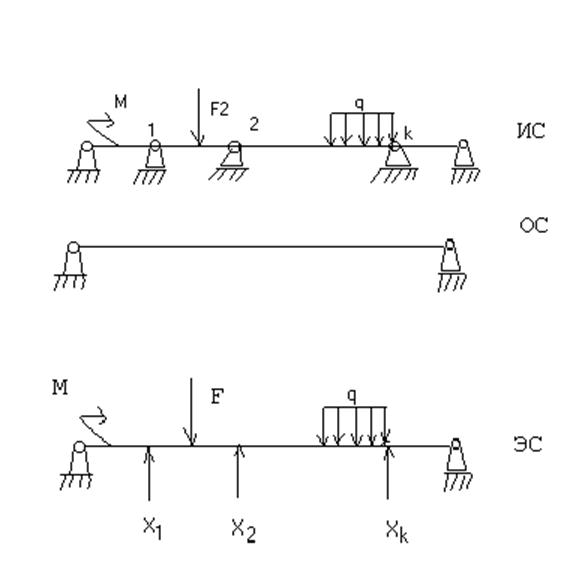
Рис. 6.13. Расчетная схема метода сил

                                                           (6.11)

Система (6.11) известна как уравнения метода сил. Это система неоднородных линейных алгебраических уравнений порядка .

                                                                                               (6.12)

Матрица [A] симметрична по теореме о взаимности перемещений. Матрица, как правило, редко заполнена, т.е. содержит много нулей. Ненулевые элементы матрицы [A] расположены вблизи диагонали, в этом случае рассматриваемая матрица называется ленточной. Указанные особенности значительно облегчают хранение и решение система неоднородных линейных алгебраических уравнений.

6.6. Использование свойств симметрии при раскрытии
 статистической неопределимости

Значительная часть современных конструкций обладает свойством симметрии. Вероятно, источником является симметрия в природе.

На симметричные конструкции могут воздействовать симметричные и кососимметричные нагрузки (рис. 6.14).

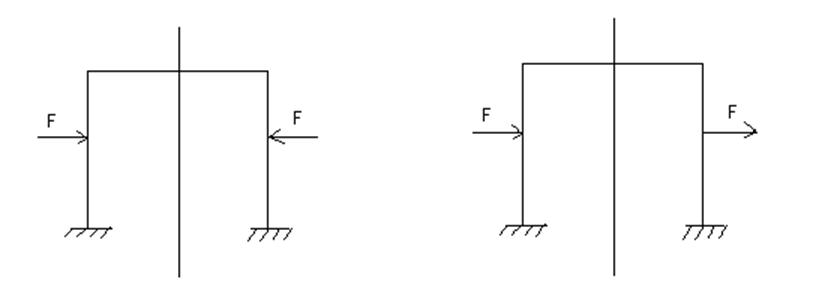
Рис. 6.14. Симметричные конструкции при воздействии симметричных
и кососимметричных нагрузок

Из трех внутренних силовых факторов, действующих в точке пересечения плоскости симметрии с конструкцией, можно образовать две группы.

1. Это X₁, X₃ (внутренние силовые факторы отброшенной части, вызывают симметричное деформирование).

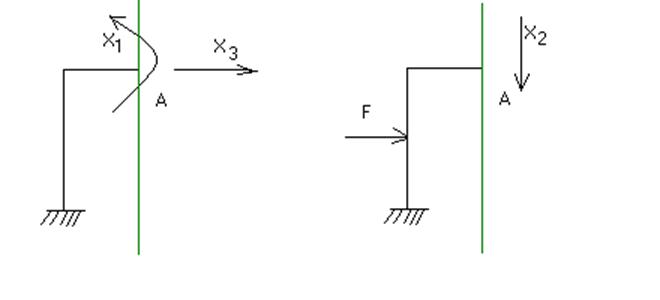
Рис. 6.15. Особенности симметричного и кососимметричного нагружений
симметричных конструкций

2.  Это кососимметричное деформирование, связанное с X₂.

Таким образом, если симметричная конструкция нагружена симметрично, то X₂=0. (X₂ – приводит к кососимметричному деформированию). Если на конструкцию действует кососимметричная нагрузка, то X₁,X₃=0.