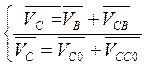Описание схемы работы машины. Шестизвенный рычажный механизм двигателя. Исходные данные для проектирования, страница 8

, где  и направлен в сторону , , , . Полученную систему уравнений решаем графически. На пересечении векторов  и   находится точка с. Положение точки S₂ центра масс шатуна 2 на отрезке bc определяем по теореме подобия 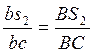  , откуда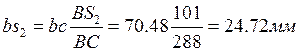

Скорость точки D группы Ассура II(4,5) определяется из системы векторных уравнений 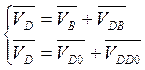, где , , .

Решение системы проводится графическим методом.

Из построенного плана скоростей вычисляем абсолютные скорости точек: V_c=(pc)μ_v=50,09*0.4=20,04м/с;

V_D=(pd)μ_v=30,5*0.4=12,2м/с;

V_s2=(ps₂)μ_v=62,98*0.4=25,19м/с;

Относительные скорости:

V_CB=(bc)μ_v=70,48*0.4=28,19м/с;

V_DB=(bd)μ_v=70,48*0.4=28,19м/с;

Угловые скорости шатунов 2 и 4:

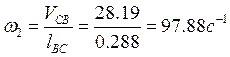
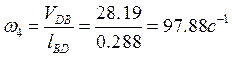
Направление угловой скорости ω₂ и ω₄ определяются направлениями соответствующих векторов относительной скорости. Которые помещены в точки С и D соответственно.

4.2.2 Построение плана ускорений

Построение начинаем с определения ускорения точки B:

 , где  -нормальное и тангенциальное ускорение соответственно.  -направлено от точки B к точке A;

  и направлен в сторону углового ускорения ε₁.

Выбираем масштабный коэффициент μ_a=100 , вычисляем отрезки, изображающие ускорение точки B:

;

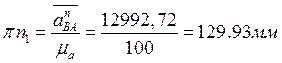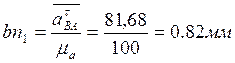
Из полюса плана ускорений π откладываем отрезок  параллельный AB, а из вершины n₁ отрезок  в направлении ε₁ (поз.3 лист 2).

Ускорение точки C группы (2,3) находится из системы векторных уравнений:

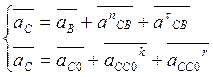, где  и  нормальное и тангенциальное ускорения точки C при вращательном движении звена 2 относительно точки B.

 и

 (точка С₀ неподвижна и принадлежит стойке);

 -кориолисово ускорение точки C;

-относительное ускорение точки C по отношению к точке B₀.

Нормальное ускорение точки C относительно точки B:

Находим отрезок, изображающий :

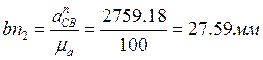
Точку S₂ центра масс шатуна находим из свойств подобия, замерив отрезок bc=66.9мм и рассчитав отрезок bs₂ .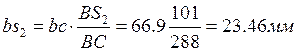

Ускорение точки D группы (4,5) определяется из системы векторных уравнений:

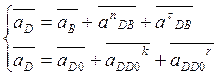, где

тогда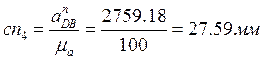

; ;

Из построенного плана ускорений вычисляем абсолютные ускорения точек:

тангенциальные составляющие относительных ускорений звеньев 2 и 4

угловые ускорения звеньев 2 и 4

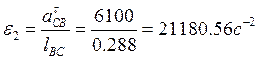
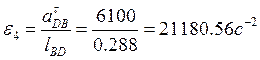
4.3 Силовой расчет исполнительного механизма

Определение реакций в кинематических парах и уравновешивающего момента выполняется кинетостатическим методом по группам Ассура, начиная с самой удаленной и заканчивая силовым расчетом механизма 1-го класса.

4.3.1 Определение внешних сил на звеньях

Первоначально определяем силы, действующие на звенья механизма.

Кривошип 1:

cила тяжести:

главный вектор сил инерции

 (т.к. центр масс кривошипа 1 неподвижен)

главный момент сил инерции

Главные вектора  и главные моменты  сил инерции направлены противоположено соответствующим линейным ускорениям центров масс  и угловым ускорениям .

Шатун 2:

Ползун 3 (поршень):

  ()

Сила давления газов на поршень 99836Н

Шатун 4:

Т.к. , , тогда , , .

Ползун 5 (поршень):

 ()

Сила давления газов на поршень 0Н

4.3.2 Силовой расчет группы (4,5)

Отсоединяем группу (4,5) и строим ее в масштабе  (поз.4 лист.2). Прикладываем к ползуну 5 внешние силы , , . Действие отсоединенных звеньев 1(кривошипа) и 6(стойки) заменяем неизвестными реакциями  (в точке B) и  (в точке D). Неизвестный вектор  представляем как сумму , где  -нормальная составляющая реакции; ;  -тангенциальная составляющая реакции; ; определяется из уравнения

                               

т.к. , то .

Следовательно, полная реакция .

Неизвестные реакции определяются из уравнения равновесия сил группы (4,5):

.

Уравнение решается графически путем построения плана сил (поз.5 лист 2).

Выбираем масштабный коэффициент:

Отрезки плана сил:

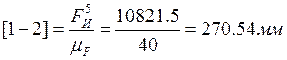
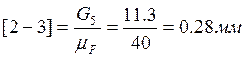
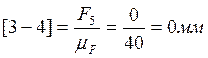
Отложив , , , из начальной точки 1 проводится направление , а из точки 4 –направление  (перпендикулярно направлению перемещения поршня 5). Точка 5 пересечения данных направлений замыкает план сил.

Из построенного плана сил группы (4,5) определяют реакции в крайних парах:

Внутреннюю реакцию  внутри шарнира D определяем из условия равновесия сил этого звена, для звена 4, уравнение будет иметь вид: