![]() м;
м;
при ![]()
![]() м;
м;
Примем
масштабные коэффициенты по оси ординат одинаковыми для двух графиков ![]() и
и ![]() :
:
![]()
а для графика ![]()
![]()
Вычисляем максимальные ординаты графиков:
перемещения
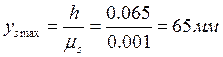 ;
;
аналога скорости
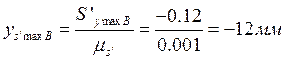
аналога
ускорения при ![]()
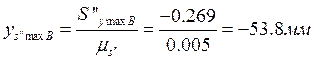
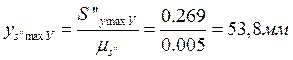 ;
;
при ![]()
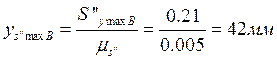
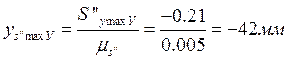 ;
;
Рассчитаем ординаты перемещения толкателя для 6 положений:
при ![]()
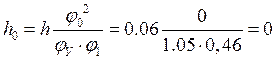 м;
м;
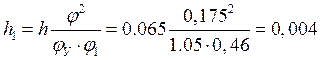 м;
м;
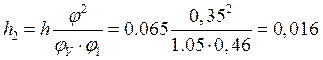 м;
м;
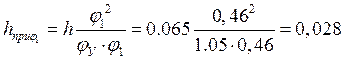 м;
м;
при ![]()
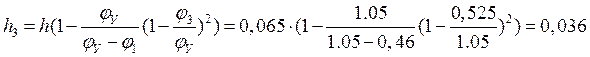 м;
м;
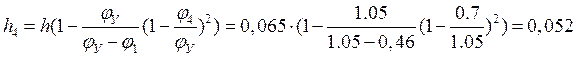 м;
м;
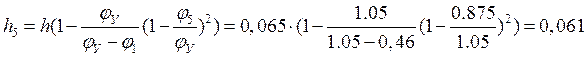 м;
м;
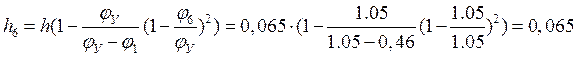 м;
м;
Рассчитываем координаты перемещения толкателя:
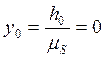 мм;
мм;
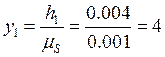 мм;
мм;
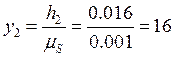 мм;
мм;
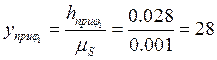 мм;
мм;
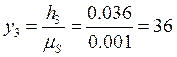 мм;
мм;
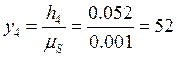 мм;
мм;
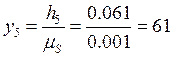 мм;
мм;
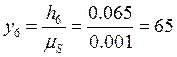 мм;
мм;
5.3. Определение основных размеров механизма
Строим графики ![]() и
и ![]() .
Максимальное линейное перемещение центра ролика коромысла
.
Максимальное линейное перемещение центра ролика коромысла ![]() .
.
Примем масштабный коэффициент ![]() и
и ![]() .
.
Определяем минимальный радиус
кулачка ![]() и межосевое расстояние
и межосевое расстояние ![]() из условия незаклинивания на фазах
удаления и возвращения. Так как высшая пара имеет силовое замыкание, то
из условия незаклинивания на фазах
удаления и возвращения. Так как высшая пара имеет силовое замыкание, то ![]() .
.
Используя график ![]() и строим положения коромысла для
фаз удаления и возвращения. На линиях, соответствующих этим положениям, от
точки M (центра ролика) откладываются векторы аналогов
скорости
и строим положения коромысла для
фаз удаления и возвращения. На линиях, соответствующих этим положениям, от
точки M (центра ролика) откладываются векторы аналогов
скорости ![]() (в масштабе
(в масштабе ![]() ), повернутые на
), повернутые на ![]() в сторону вращения кулачка. Из
концов этих векторов проводятся лучи под углами
в сторону вращения кулачка. Из
концов этих векторов проводятся лучи под углами ![]() к
положениям коромысла. Центр вращения кулачка выбирается в зоне, свободной от
пересечения лучей. Из рис.4 лист 2. минимальный радиус кулачка
к
положениям коромысла. Центр вращения кулачка выбирается в зоне, свободной от
пересечения лучей. Из рис.4 лист 2. минимальный радиус кулачка ![]()
![]()
![]() .
.
5.4. Построение центрового профиля кулачка
Строим центровой профиль
кулачка. Выбирается масштаб построения ![]() .
Откладывается линия центров
.
Откладывается линия центров ![]() . Из точки
. Из точки ![]() через точки
через точки ![]() , проводятся концентрические дуги.
От линии центров
, проводятся концентрические дуги.
От линии центров ![]() в сторону, противоположенную
вращению кулака, откладываются фазовые углы
в сторону, противоположенную
вращению кулака, откладываются фазовые углы ![]() .
Дуги максимального радиуса, стягивающие углы
.
Дуги максимального радиуса, стягивающие углы ![]() и
и
![]() , делятся на части согласно графику
, делятся на части согласно графику
![]() . Полученные точки
. Полученные точки ![]() радиусом, равным длине коромысла
радиусом, равным длине коромысла ![]() , сделать засечки по
соответствующим коническим дугам. Соединив плавной кривой точки 1,2,…,12,
получают центровой профиль кулачка на фазах удаления и возвращения. На фазах
дальнего стояния профиль кулачка очерчивается дугой максимального радиуса, на
фазах ближнего стояния дугой минимального радиуса
, сделать засечки по
соответствующим коническим дугам. Соединив плавной кривой точки 1,2,…,12,
получают центровой профиль кулачка на фазах удаления и возвращения. На фазах
дальнего стояния профиль кулачка очерчивается дугой максимального радиуса, на
фазах ближнего стояния дугой минимального радиуса ![]() .
.
Строим действительный профиль
кулачка. Радиус ролика выбирается наименьшим из двух условий: ![]() ;
; ![]() .
Окончательно принимаем
.
Окончательно принимаем ![]() . Определим минимальный
радиус кривизны центрового профиля
. Определим минимальный
радиус кривизны центрового профиля ![]() как радиус
вписанной окружности выпуклого участка профиля кулачка, где кривизна его
окажется наибольшей. На этом участке произвольно выбираем три точки
как радиус
вписанной окружности выпуклого участка профиля кулачка, где кривизна его
окажется наибольшей. На этом участке произвольно выбираем три точки ![]() и соединяем их двумя хордами. В
середине хорд восстанавливаем к ним перпендикуляры, точку пересечения которых M
принимаем за центр вписанной окружности.
и соединяем их двумя хордами. В
середине хорд восстанавливаем к ним перпендикуляры, точку пересечения которых M
принимаем за центр вписанной окружности.
5.5. Построение графика зависимости угла давления
Строим график зависимости угла
давления ![]() от угла поворота для фаз удаления
и возвращения, так как высшая пара.
от угла поворота для фаз удаления
и возвращения, так как высшая пара.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
34 |
43 |
38 |
20 |
3 |
-12 |
-23 |
-33 |
-41 |
-37 |
-17 |
12 |
Из графика ![]() следует, что
следует, что ![]() , следовательно, условие синтеза
, следовательно, условие синтеза ![]() выполняется.
выполняется.
6. Расчет замыкающей пружины
Чтобы толкатель при больших
ускорений не отрывался от профиля кулачка под действием силы инерции,
предусматривается силовое замыкание высшей кинематической пары пружиной
растяжения сжатия. Жесткость пружины должна быть такой, чтобы сила упругости
пружины ![]() превышала максимальную отрывающую
силу инерции коромысла, т.е.
превышала максимальную отрывающую
силу инерции коромысла, т.е. ![]() .
.
Максимальную силу инерции
определяем по рассчитанному ранее максимальному аналогу ускорения ![]() .
.
![]() ,
где
,
где
![]() -масса
толкателя;
-масса
толкателя;
![]() -угловая скорость кулачка;
-угловая скорость кулачка;
Так как сила инерции ![]() противоположенная ускорению
толкателя (аналогу ускорения
противоположенная ускорению
толкателя (аналогу ускорения ![]() ), то график
силы инерции в функции перемещения толкателя
), то график
силы инерции в функции перемещения толкателя ![]() строится
на основании графиков аналога ускорения
строится
на основании графиков аналога ускорения ![]() и
перемещения
и
перемещения ![]() исключением
исключением ![]() . Строим график для фазы удаления.
. Строим график для фазы удаления.
![]() ,
, ![]() .
Предварительное натяжение пружины
.
Предварительное натяжение пружины ![]() . Выбираем
масштабные коэффициенты
. Выбираем
масштабные коэффициенты ![]() и
и ![]() , производим построения (поз.7
лист3). Соединив точки a и b, получим зависимость
, производим построения (поз.7
лист3). Соединив точки a и b, получим зависимость ![]() . Максимальная сила пружины
. Максимальная сила пружины ![]() . Жесткость пружины
. Жесткость пружины 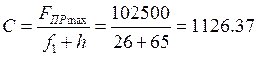 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.