Тогда максимальное изменение
![]()
![]() .
.
Необходимая величина постоянной
части приведенной части приведенного момента инерции ![]() ,
обеспечивающая более равномерное вращение кривошипа 1 с заданным коэффициентом
неравномерности
,
обеспечивающая более равномерное вращение кривошипа 1 с заданным коэффициентом
неравномерности ![]() равна
равна
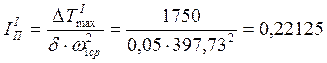
![]() .
.
Момент инерции маховика на валу кривошипа, который обеспечивает необходимую равномерность вращения
![]()
![]() .
.
Выбрав форму маховика – диск диаметром
![]() м, определяем его маховый момент
м, определяем его маховый момент ![]() и примерную массу
и примерную массу ![]()
![]()
![]() ;
;
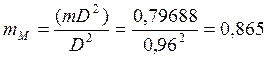
![]() .
.
3.10. Динамический анализ движения машины
Необходимо определить
действительные угловую скорость ![]() и угловое
ускорение
и угловое
ускорение ![]() звена приведения (кривошипа 1)
внутри цикла после установки маховика, обеспечивающих расчетную величину
звена приведения (кривошипа 1)
внутри цикла после установки маховика, обеспечивающих расчетную величину ![]() .
.
Угловая скорость ![]() может определяться из выражения
кинетической энергии
может определяться из выражения
кинетической энергии ![]() вращающихся звеньев с
вращающихся звеньев с ![]() .
.
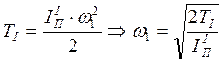 .
.
Согласно методу Н.И. Мерцалова
построенный график ![]() является приближенно и
графиком изменения угловой скорости
является приближенно и
графиком изменения угловой скорости ![]() , отсчитанной от
среднего значения
, отсчитанной от
среднего значения ![]() . Поэтому для
графического определения
. Поэтому для
графического определения ![]() отрезок ab на
графике
отрезок ab на
графике ![]() делится пополам, и из точки (ab/2) проводится
горизонтальная прямая, которая соответствует значению
делится пополам, и из точки (ab/2) проводится
горизонтальная прямая, которая соответствует значению ![]() .
От этой средней прямой в расчетном положении №8 замеряем ординату
.
От этой средней прямой в расчетном положении №8 замеряем ординату ![]() до кривой
до кривой ![]() :
:
![]() мм. Тогда угловая скорость
мм. Тогда угловая скорость ![]() в этом положении будет равна
в этом положении будет равна
![]() , где
, где ![]() -
масштабный коэффициент угловой скорости графика
-
масштабный коэффициент угловой скорости графика ![]() :
:
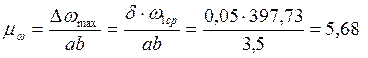
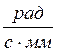 .
.
Для расчетного положения №8:
![]()
![]() .
.
Угловое ускорение ![]() звена 1 определяется из уравнения
движения звена приведения в дифференциальной форме
звена 1 определяется из уравнения
движения звена приведения в дифференциальной форме
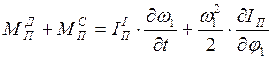 .
.
Отсюда
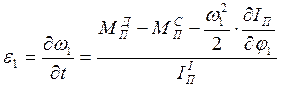 .
.
Для расчетного положения №8:
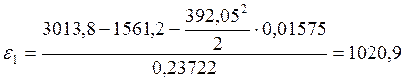
![]() , где
, где ![]() ,
,![]() - приведенные моменты сил движущих
и сил сопротивления в расчетном положении,
- приведенные моменты сил движущих
и сил сопротивления в расчетном положении,
![]() -
действительная угловая скорость в расчетном положении.
-
действительная угловая скорость в расчетном положении.
![]() - полный приведенный момент инерции в расчетном
положении,
- полный приведенный момент инерции в расчетном
положении,
![]()
![]() ;
;
![]() - производная
от
- производная
от ![]() по
по ![]() ,
определяемая графически из графика
,
определяемая графически из графика ![]() :
:
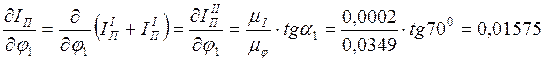
![]() ;
;
![]() -
угол наклона касательной, проведенной к графику
-
угол наклона касательной, проведенной к графику ![]() в
расчетном положении №8 (поз. 4, лист 1),
в
расчетном положении №8 (поз. 4, лист 1), ![]() .
.
4. Динамический анализ рычажного механизма
4.1 Задачи и методы динамического анализа механизма
Задачей динамического анализа исполнительного механизма (шестизвенного рычажного механизма ДВС) является:
1) определение истинных скоростей и ускорений точек и звеньев механизма с учетом неравномерности вращения кривошипа;
2) определение реакций во всех кинематических парах механизма и определение уравновешивающего момента, действующего на коленчатый вал ДВС со стороны отсоединенной части трансмиссии автомобиля.
Поставленные задачи решаются графо-аналитически путем построения плана положений механизма, планов скоростей и ускорений, планов сил. В основу расчетов положен кинетостатический метод, основанный на принципе Даламбера. В соответствии с этим принципом, если к числу активных сил и реакций связей, действующих на механическую систему, приложить силы инерции (главные векторы и главные моменты сил инерции) звеньев, то система рассматривается как находящаяся в равновесии и вместо уравнений движения можно записать уравнения равновесия (статики).
Для определения сил инерции
необходимо знать ускорения центров масс и угловые ускорения звеньев. Поэтому
силовому анализу предшествует кинематический анализ по известному закону ![]() и
и ![]() движения
звена 1.
движения
звена 1.
4.2 Задачи и методы динамического анализа
Расчет производится для
положения №8, заданного обобщенной координатой ![]() .
Изображаем схему механизма в данном положении, используя масштабный коэффициент
.
Изображаем схему механизма в данном положении, используя масштабный коэффициент
![]() и чертежные отрезки АВ=40мм, BC=144мм,
CD=144мм, BS2=50.5мм, рассчитанные в п. 3.4.1. Построение выполняем методом засечек
для заданной обобщенной координаты (поз.1 лист 2). Значения угловой скорости и
углового ускорения кривошипа 1 в положении №8 равны:
и чертежные отрезки АВ=40мм, BC=144мм,
CD=144мм, BS2=50.5мм, рассчитанные в п. 3.4.1. Построение выполняем методом засечек
для заданной обобщенной координаты (поз.1 лист 2). Значения угловой скорости и
углового ускорения кривошипа 1 в положении №8 равны: ![]() .
Стрелками указываем их направление на схеме.
.
Стрелками указываем их направление на схеме. ![]()
![]() .
.
4.2.1 Построение плана скоростей
Для построения плана скоростей
необходимо определить скорости точек B кривошипа: ![]()
Выбираем масштабный коэффициент скорости
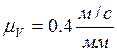
Отрезок pb изображающий скорость точки B находится по формуле
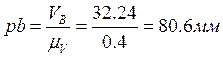
![]()
![]() Построение плана скоростей осуществляется в
соответствии с формулой II(2,3) I(1,6) II(4,5).
Построение плана скоростей осуществляется в
соответствии с формулой II(2,3) I(1,6) II(4,5).
Для группы Ассура II(2,3) запишем векторные уравнения скорости точки С:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.