Описание схемы работы машины. Шестизвенный рычажный механизм двигателя. Исходные данные для проектирования, страница 4

3.5. Динамическая модель машинного агрегата

Для упрощения решения вопросов динамики реальная схема машинного агрегата автобуса заменяется одномассовой эквивалентной динамической моделью. Используем динамическую модель с вращающимся звеном приведения, в качестве которого принят кривошип 1 (рис. 3.4)

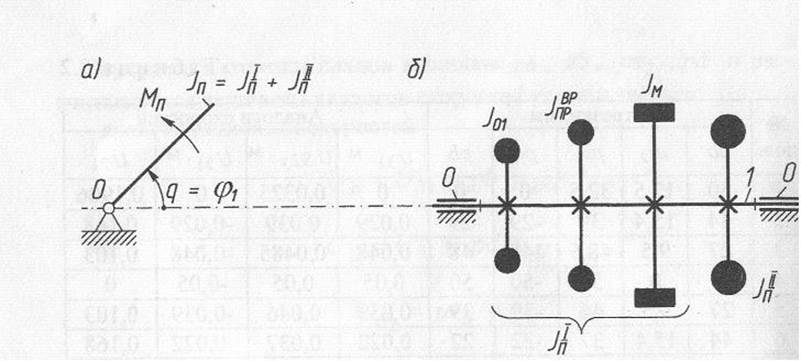
Рис.3.4

Закон движения звена приведения должен быть таким же, как и у кривошипа 1 рычажного механизма, т.е. обобщенная координата , угловая скорость , угловое ускорение . Для этого все инерционные параметры звеньев механизма заменяем приведенным моментом инерции , а силовые параметры на звеньях заменяются приведенным моментом сил .

Приведенный момент инерции  - это условный момент инерции звена приведения, кинематическая энергия  которого равна сумме кинетических энергий  всех подвижных звеньев машинного агрегата, т.е  , или

,

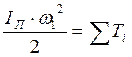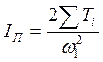
Приведенный момент инерции  представляем в виде двух частей (рис. 3.4, б)

, где  - постоянная составляющая  от вращающихся звеньев с постоянными передаточными отношениями  u = i = const, поэтому ;

  - переменная составляющая  от звеньев с переменными аналогами скоростей i=u.

Постоянная  в соответствии с рис.3.4, б состоит из следующих слагаемых:

, где  - момент инерции кривошипа 1,

- приведенный к валу 1 момент инерции вращающихся звеньев машины.

,

 - известная составляющая ,

;

 - момент инерции маховика.

3.6. Определение переменной составляющей приведенного момента инерции

Переменная составляющая  приведенного момента инерции определяется из равенства кинетических энергий звена приведения 1 и звеньев 2, 3, 4, 5 рычажного механизма

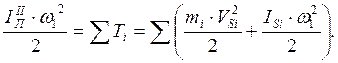
Так для звена 4 , , то равенства кинетических энергий в соответствии со схемой запишется так

.

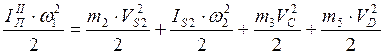Отсюда

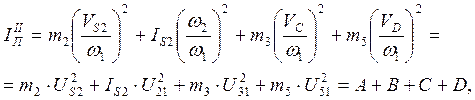
где .

Рассчитаем  для положения №8:

,

,

,

,

.

Результаты расчетов  для остальных 12-ти положений представлены в табл. 3.3. По результатам расчетов строим график переменной составляющей в функции угла  (поз. 4. лист 1).

Масштабный коэффициент момента инерции

.

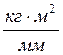Ординаты графика 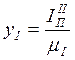, , 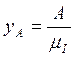, , 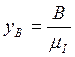 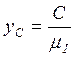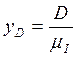сводим в табл. 3.3.

Таблица 3.3

№ пол.	A,	, мм	B,	, мм	C,	, мм	D,	, мм	,	,мм
1	0,00779	38,9	0,00314	15,7	0	0	0	0	0,01093	54,7
2	0,01125	56,3	0,00240	12	0,00284	14,2	0,00106	5,3	0,01755	87,8
3	0,01720	86	0,00080	4	0,00721	36,1	0,00402	20,3	0,02923	146,2
4	0,01843	92,2	0	0	0,00736	36,8	0,00736	36,8	0,03315	165,8
5	0,01444	72,2	0,00080	4	0,00405	20,3	0,00721	36,1	0,0265	132,5
6	0,00967	48,4	0,00240	12	0,00106	5,3	0,00284	14,2	0,01597	79,9
7	0,00779	38,9	0,00314	15,7	0	0	0	0	0,01093	54,7
8	0,00967	48,4	0,00240	12	0,00106	5,3	0,00284	14,2	0,01597	79,9
9	0,01444	72,2	0,00080	4	0,00405	20,3	0,00721	36,1	0,0265	132,5
10	0,01843	92,2	0	0	0,00736	36,8	0,00736	36,8	0,03315	165,8
11	0,01720	86	0,00080	4	0,00721	36,1	0,00405	20,3	0,02923	146,2
12	0,01125	56,3	0,00240	12	0,00284	14,2	0,00106	5,3	0,01755	87,8