Анализ качества использования рабочей силы на производственном участке, страница 14

3.2. Используя матрицу парных коэффициентов, строим систему линейных уравнений.

rx₁y₁=b₁+b ₂rx₁x₂+b ₃rx₁x₃+b₄rx₁x₄

rx₂y₁=b ₁rx₂x₁+b ₂+b₃rx₂x₃+b₄rx₂x₄

rx₃y₁=b₁rx₃x₁+b₂rx₃x₂+b₃+b₄rx₃x₄

rx₄y₁=b₁rx₄x₁+b₂rx₄x₂+b₃rx₄x₃+b₄

Решив систему уравнений одним из известных методов определить значение коэффициентов регрессии в стандартизованном масштабе (b₁, b₂, b₃, b₄). В качестве стандартов выступает среднеквадратическое отклонение. Коэффициент регрессии b показывает насколько изменится функция при изменении аргумента на 1 свою . Коэффициент b может принимать любые значения. Чем выше коэффициент b, тем больше влияние оказывает фактор на функцию.

b₁₌0,078615, b₂=-0,19914, b₃,=-0,00368, b₄ =-0,04877.

Следовательно, связь между признаками незначительная. Воздействие на результативный признак (выработку) носит обратный характер по показателям «стаж», «квалификация», «образование»; параметр «возраст» находится в прямой зависимости.

3.3. Определение значений коэффициентов регрессии в натуральном масштабе (b1, b2, b3, b4).

Коэффициент “b” показывает, как изменяется функция при изменении аргумента на единицу своего изменения.

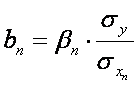                           (7)

Получаем:

b₁=0,213738,  b₂ =-0,8123, b₃=-0,1,  b₄= -0,618