Магнитное поле в вакууме. Основные определения и формулы. Магнитное поле равномерно движущегося заряда

 МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

F! = qE! +q v B^_^!, ^!_  сила Лоренца.

На покоящийся электрический заряд магнитное поле не действует. Магнитная сила перпендикулярна скорости, поэтому работы над зарядом она не совершает.

_{B =} ^µµ4π⁰ _q^{[v r! !}r^,₃ ^]  магнитное поле равномерно движущегося заряда, где µ₀  ^!

магнитная постоянная, µ  магнитная проницаемость среды (для вакуума µ=1), ^µ =10⁻⁷ Гн/м, _r^!  радиус-вектор, проведенный от заряда q к точке наблюдения.

Принцип суперпозиции  магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности: _B^! = ∑_B^!_i .

Закон Био  Савара  Лапласа: dB! = µµ₄π0 !j r dV, _r!3 или dB! = µµ4π0 I dl r r!3, !  нахождение магнитного поля, создаваемого постоянными электрическими токами, где ^!jdV и _Idl^!  объемный и линейный элементы тока.

Согласно принципу суперпозиции: ! µµ _ ^!j r dV, !_                                                            ! _µµ I dl r_ ^!, ^!_ .

Теорема Гаусса для поля _B^! : Поток вектора _B^! сквозь любую замкнутую поверхность равен нулю: "∫ BdS^{! !} = 0.

Следствие: поток вектора  _B^! сквозь поверхность S , ограниченную некоторым замкнутым контуром, не зависит от формы поверхности S . Теорема о циркуляции вектора _B^! (для магнитного поля постоянных токов в вакууме): Циркуляция вектора _B^! по произвольному контуру Γ равна произведению µ₀ на алгебраическую сумму токов, охватываемых контуром Γ : "∫ Bdl^{! !} = µ₀I , где I = ∑I_k .

Т.к. циркуляция вектора _B^! не равна нулю, значит поле _B^! не потенциально, его называют вихревым или соленоидальным.

Теорема Гаусса для поля _B^! в дифференциальной форме: _∇^{! !}B = 0, т.е. дивергенция поля _B^! всюду равна нулю. Значит, магнитное поле не имеет источников          (магнитных зарядов). Магнитное поле порождается электрическим током.

Дифференциальная      форма       теоремы      о      циркуляции: ∇^{! !}B = µ₀ ^!j ,

                 e^!x      e^!y      e^!z

! !

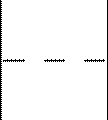_∇×B ₌ ∂∂x ∂∂y ∂∂z .

                  Bx        By        Bz

Сила Ампера:

Закон Ампера: каждый носитель тока испытывает действие магнитной силы: dF^! = _ ^!j B dV, ^!_ или dF^! = I dl B_ ^!, ^!_ .

Силы, действующие на токи в магнитном поле называют амперовыми или силами Ампера. 

F! = I"∫ _dl B^!, ^!_   сила, действующая на контур с током.

Если магнитное поле однородно, то вектор _B^! можно вынести за знак интеграла, "∫ dl^! = 0 и, следовательно F^! = 0 , т.е. результирующая сила

Ампера равна нулю в однородном магнитном поле.

Магнитный момент _p^!_m = _ISn^! , где I  ток, S  площадь, ограниченная контуром, _n^!  положительная нормаль к контуру.

F p  сила, действующая на контур с током в неоднородном магнитном поле, где p_m  модуль магнитного момента контура,   производная вектора _B^! по направлению нормали _n^! или по направлению вектора p^!_m .

M! = ^_p^!_m,B^!_  момент сил, действующих на контур с током, где p^!_m  магнитный момент контура с током.

Для плоского контура p^!_m = ISn^! , если виток не плоский, то p^!_m = I dS_∫ ^!

(интеграл берется по поверхности S «натянутой» на контур с током).

δA = IdΦ  работа при перемещении контура с током, где dΦ  приращение магнитного потока сквозь контур при данном перемещении.

Работа амперовых сил при полном перемещении контура с током от начального положения 1 до конечного 2: A 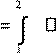Id .

Если ток I  постоянный, то A = I (Φ −Φ_{2 1}), где Φ₁ и Φ₂  магнитные потоки сквозь контур в начальном и конечном положениях.

ЗАДАЧИ Принцип суперпозиции:

1. К двум точкам проволочного кольца радиуса r подсоединены два параллельных очень длинных проводника, соединенных с удаленным источником тока. По прямому проводнику течет ток I . Найти индукцию магнитного поля в центре кольца.

Решение:

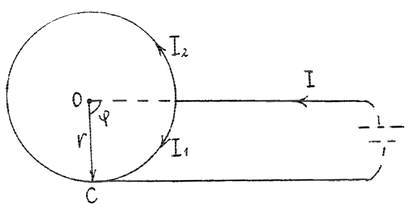
Текущий по      радиальному проводнику ток I не создает магнитного поля в центре О. В точке соединения А этот ток разделяется на токи I₁ и I₂ , обтекающие точку О по дугам в противоположных направлениях.

Падение напряжения на обеих дугах одинаково (они подсоединены в точках А и С параллельно), а сопротивления дуг пропорциональны их

длинам l1 и l2 , т.е. II12 = RR12 = ll12 = 2πϕ−ϕ.

Текущий по радиусу r ток I создает в центре кольца магнитное поле с индукцией B_кольца = ^{µ I} . Если ток течет по части кольца, т.е. по дуге с углом ϕ, то индукция пропорциональна длине этой дуги: _B^Bкольца^дуги = ₂^ϕ_π . Поэтому для полей B₁ и B₂ , созданных в точке О токами I₁ и I₂ , можно записать с учетом первой формулы _B^B12 = _I2 ₍₂^I_{π ϕ}^1ϕ_{− )} =1, т.е. поля B₁ и B₂ равны по величине, направлены противоположно и в сумме равны нулю. Поле в точке О создается только током, текущим по нижнему полубесконечному прямому проводнику: B_{0 =} ^{µ I} .