Магнитное поле в вакууме. Основные определения и формулы. Магнитное поле равномерно движущегося заряда, страница 4

B = µqv .

Fлор = qvB = µ0q v2 22 = Fкул = 1 q2 .

                             4πr                  4πε r

Отсюда v² = ¹ , v = ¹ = c  скорость света.

                               µ0ε0                      µε0 0

Материальные частицы с m ≠ 0 не могут двигаться с такой скоростью. Здесь показано, что F_магн $ F_элект взаимодействия и эти силы сравниваются только при v = c . Это получено для нерелятивистских частиц и F_кул>F_лор. Ответ: частицы разлетаются.

10.  Смоделировать траекторию заряженной частицы в магнитном поле можно, натянув в зазоре магнита проволоку с током. С какой силой F надо натянуть проволоку с током I =1 А, чтобы имитировать траекторию протона с энергией W =1 МэВ?

Решение:

 

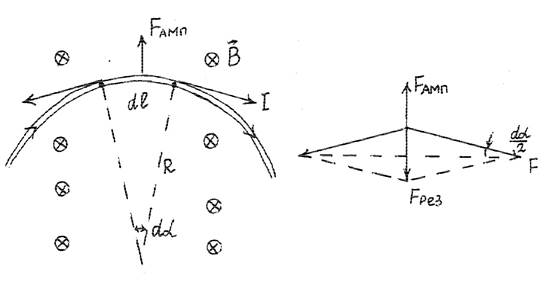
На изогнутый элемент тока dl = Rdα (R  радиус кривизны) действуют с двух концов силы натяжения F . Их результирующая равна

F_рез  F F   Fd        .

Она уравновешена силой Ампера: F_А = F_рез или IdlB = Fdα (dl = Fdα), F = IRB.

Но протоны в постоянном поле летят по окружности: m_p ^v_R² = evB (evB  сила Лоренца) с радиусом R = ^{m v}_eB^p , где m_p ^v₂² =W  энергия протона. v = ²m^Wp , R = ²_eB^mp и сила натяжения F = ^I_l 2m W_p =0,14 Н.

Ответ: F = ^I_l   2m W_p  =0,14 Н.

11.  Частицы с зарядом q и массой m ускоряются в циклотроне так, что максимальный радиус орбиты равен r . Частота генератора циклотрона ν, эффективное напряжение между дуантами U . Пренебрегая шириной зазора между дуантами найти полное время процесса ускорения частицы и найти приближенное значение пройденного ею при ускорении пути при величинах: q =1,0⋅10⁻²⁰ Кл, m =10⁻²⁷ кг, r =1 м, ν =10 МГц, U = 20 кВ.

Решение:

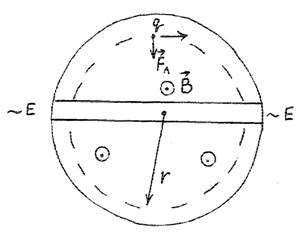В дуантах частица движется по окружности с радиусом r , где

m v2 = Fл = qvB, r = mvqB . r

Период обращения частицы: 

^T2 ₌ ^πv^r  при движении от зазора до зазора, т.е. T = ²_qB^πm не зависит от скорости частицы, т.о. ν = _T¹ = ₂^qB_πm и B = ^{2π ν}_q^m  индукция поля в циклотроне.

При заданном r конечная скорость частицы после ускорения v ₌ ^rqB_m , а энергия W = ^mv₂ ² = 2π ν²m ²r² приобретается частицей скачками. Каждый раз, проходя разность потенциалов U в зазоре, она приобретает энергию

W₁ = qU , т.е. W = NW₁, где N = ^W ₌ ^{2π ν2m 2r2}             число пролетов через

                                                                                     W₁                qU

ускоряющий зазор.

Это число N .

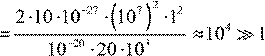Т.к. при полном обороте частица дважды проходит зазор, а период оборота не зависит       от      скорости     (постоянен),         то время          ускорения t 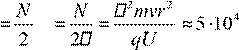T          секунд.

Пройдя путь n раз частица имеет энергию W_n = nqU ₌ ^mv₂ⁿ² и скорость vn = 2nqUm .

До следующего зазора она пройдет путь s_n = v_n ^T₂ = ₂^v_νⁿ , т.е. общий путь

частицы S 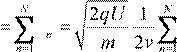 s   n .

Т.к. N &1, то считая 1≈ dn , находим ^∑n^N=1 n ≈ ^N∫0   ndn = ₃² n³² 0^N = ₃² N ³² или

3

s = 31ν 2qUm N 32 = 31ν 2qUm  2π ν2qUm 2r2  2 = 4m3π νqU2r3                 2 ≈ 2⋅104 м.

Ответ: t = ^π2_qU^mvr2 ≈ 5⋅10⁴ секунд, s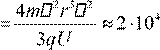 м.

Магнитный момент контура с током:

12. Равномерно заряженный с поверхностной плотностью σ диэлектрический диск радиуса R вращается с угловой скоростью ω вокруг своей оси. Определить его магнитный момент.

Решение:

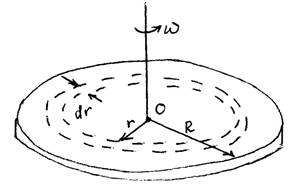Разбиваем диск на бесконечно узкие кольца радиуса r и толщины dr . Заряд на таком кольце dq =σ π⋅2 rdr при вращении диска делает один оборот за время ∆ =t  и образует круговой ток dI = ^dq_∆t =σωdr.

Магнитный момент этого тока направлен вдоль оси диска и равен dp_m = dI S⋅ , где S =πr²  площадь, охватываемая током dI .

Складывая магнитные моменты всех колец, т.е. интегрируя по r , получим магнитный момент всего диска: ^{R R4} .

Ответ: pm = πσω4R4 .

13. Равномерно заряженный с плотностью ρ шар радиуса R вращается с угловой скоростью ω вокруг своей оси. Определить его магнитный момент.