Магнитное поле в вакууме. Основные определения и формулы. Магнитное поле равномерно движущегося заряда, страница 3

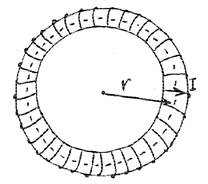
Внутри катушки линии индукции образуют замкнутые кольца. Выбрав контур интегрирования, совпадающий с таким кольцом (с осью катушки) и охватывающий все N витков с током I , получим из теоремы о циркуляции "∫ B dl_O         = 2πr B⋅ _O = µ₀NI или

BO = µ ^NI .

Но, если диаметр витков достаточно мал (d $ r), то можно считать, что тот же ток I обтекает центр тороида О практически по круговому контуру радиуса r и создает В центре (в точке О) поле B_Ц ≈ ^µ₂⁰_r^I (поле кругового тока). Это можно показать, используя закон Био  Савара  Лапласа. В итоге _B^BOЦ ≈ _π^N ≈1000.

Ответ: _B^BOЦ ≈ _π^N ≈1000.

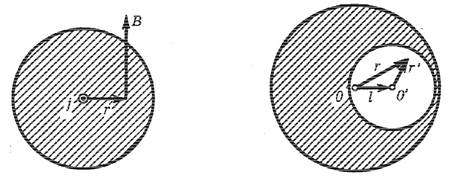
7. Внутри однородного длинного провода, круглого сечения имеется круглая цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние l. По проводу течет постоянный ток плотности ^!j . Найти магнитную индукцию _B^! внутри полости.

Решение:

Искомую величину можно представить согласно принципу суперпозиции как B^! = B^!₀ − B^!′, где B^!₀  магнитная индукция в том случае, если бы B^!′  магнитная индукция поля в той же точке от тока, текущего по части провода, которую мы удалили, образовав полость круглого сечения.

Т.о., задача предусматривает, прежде всего, вычисление магнитной индукции _B^! внутри сплошного провода на расстоянии r от его оси.

Воспользовавшись теоремой о циркуляции, запишем 2π µπrB =      ₀ r j² , откуда

B ₌ ^µrj . Последнее равенство можно представить в векторной форме

!        ^!

B _{= µ}0  jr2! .

 

Представив теперь по этой формуле _B^!₀ и _B^!′, найдем их разность:

B = µ !jr! − µ !jr!′ = µ2 !j r, ! !−r′ , r! = l! + r! , откуда r! !− r′ = l! и B! = µ  2 !

            0         0            0                                                                                                                                   0 !jl! .

           2              2

Т.о., в нашем случае магнитное поле _B^! в полости является однородным, и если ток течет к нам, то поле _B^! направлено в плоскости рисунка вверх. ^!!

Ответ: B^! = µ0 ^ jl₂ _ .

Сила Ампера, сила Лоренца:

8. Может ли заряженная частица в скрещенных магнитном и электрическом полях с индукцией _B^! и напряженностью _E^! двигаться равномерно и прямолинейно? В каком случае, какова при этом скорость _v^! частицы?

Решение:

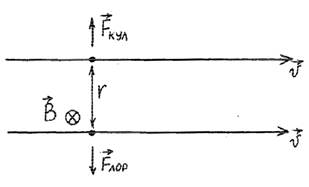
В поле _E^! на частицу действует сила Кулона _F^!_кул = _qE^! . Чтобы частица двигалась равномерно и прямолинейно кулоновскую силу должна уравновешивать другая сила. Это сила Лоренца: F^!_лор = q v B^_^!, ^!_ .

Т.е. qE^! = q v B_^!, ^!_ или E^! = _v B^!, ^!_           условие равновесия и прямолинейного движения.

Чтобы выделить скорость _v^! домножим левую и правую часть скалярно на

E B! !⋅ = _v B^!, ^{! !}_⋅B: E B^{! !}⋅ = _v B^!, ^{! !}_⋅B и учтем правило циклической перестановки a b^!, ^!_⋅c^! − _b c^!, ^{! !}_⋅a =[c a b^{! !}, ]⋅ ^! , т.е. E B^{! !}⋅ = _B B^{! !}, _⋅v^! = 0, (_B B^{! !}, _ = 0) поля E^! и B^! _

должны быть перпендикулярны.

Домножим на v^! : E v^! ⋅ ^! = _v B^!, ^!_⋅v^! =[v v^{! !}, ]⋅B^! = 0 ([v v^{! !}, ]= 0), т.е. v^! ⊥ E^! .

Разложим скорость          v^! на две составляющие:      v^!_⊥ ⊥ B^! ,    v^!_% % B^! , тогда

_v B^!, ^!_ = _v^!_⊥,B^!_ = E^! или v B_⊥ sin90^# = E (sin90^# =1).

Ответ: , v_%  любое.

9. Могут ли две одинаковые свободные заряженные частицы постоянно находиться в вакууме на постоянном расстоянии друг от друга?

Решение:

 

Заряды расталкивает сила Кулона и притягивает равная ей по величине сила Лоренца, т.к. движущиеся в одну сторону заряды  это «одноименно» направленные, т.е. притягивающиеся токи.

                                                                                                                                          11

Поле _B^! ₌ ^{µ q v r[}_r^{! !}₃^{, ]} создается одной движущейся частицей возле другой, т.е.