Магнитное поле в вакууме. Основные определения и формулы. Магнитное поле равномерно движущегося заряда, страница 5

Решение:

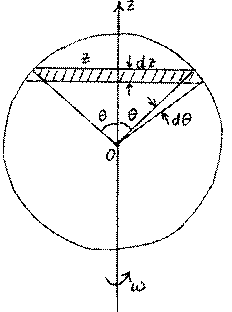Разбиваем шар на узкие круги толщины dz и радиуса r = Rsinθ.

                                                             Т.к. z = Rcosθ, то dz =  ^dR_d^cos_θ^θ dθ = Rsinθθd  = dz.

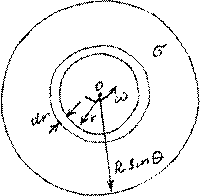Заряд на круге равен ρπ⋅ r dz²    . Практически на круге с бесконечно малой толщиной    dz       этот   заряд   распределен          с поверхностной плотностью σ = ρdz.

На вращающемся круге выделяем кольца толщиной dz с зарядом dq =σ⋅S_кольца =σ π⋅2 rdr .

Этот движущийся заряд создает тонкий круговой ток         dI          rdr, где         T         период вращения.

Магнитный момент этого тока dp_m = dI ⋅π πωσr² = r dr³ . Тогда магнитный момент всего круга: dpmкруга = ∫dpmкольца = ^Rsin∫^θπωσr dr3 = πωρdz R⁽ sinθ)⁴ ,

                                               0                                                         4

а магнитный момент всего шара:

pmшара 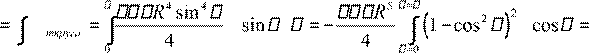dp R                                                                     d                                            d

= −    −∫(1− x2 )2 dx = πωρ4R5 −∫11dx −2−∫12 x dx2 + −∫11x dx4         = πωρR5 1

               4      1

= πωρ4R5 x1−1 − 23x3 1−1 + x55 1−1 =      πωρ4R5 2 − 43 + 52 = 145πωρR5 

Ответ: pmшара = 145πωρR5 .

14. Определить период малых колебаний свободно подвешенного магнитного бруска длиной l =10 см в магнитном поле Земли с горизонтальной составляющей индукции B_Г = 2⋅10⁻⁵ Тл. Плотность стали

ρ= 7,8⋅10³ кг/м³, а остаточная индукция B₀ =1 Тл.

Решение:

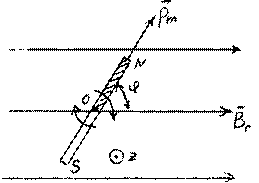Момент сил, действующий на магнитный момент p^!_m бруска M _z = −p B_{m       Г} sinϕ стремится развернуть брусок по направлению _B^!_Г .

Уравнение колебаний: I ^d_dt^2ϕ₂ = M _z = −p B_{m Г} sinϕ, где I = ^ml₁₂² , m  масса бруска, sinϕ ϕ≈ для малых колебаний.

Тогда ddt2ϕ2 +12mlp Bm2 Г ϕ= 0.

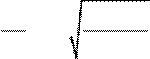12p Bm2 Г =ω02 , т.е. T = ω2π0 = 2π 12mlp Bm2 Г . ml

Очень тонкий длинный магнит с остаточной индукцией B₀ внутри эквивалентен тонкому соленоиду того же сечения S и длины l в котором N витков и по которому течет ток I , создающий внутри соленоида то же поле B₀ = µ₀ ^IN_l .

Магнитный момент одного витка p всего соленоида p_m = NIS , т.е. p_m = 0 0

это формула для магнитного момента тонкого магнита объемом с остаточной индукцией B₀ .

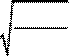Подставляя в T и, учитывая, что _p^mm ^{= ρµ}_B0⁰ и T =πl ₃^ρµ_{B B}0 ⁰Г = 4,02 с.

Ответ: T =πl ₃^ρµ_{B B}0 ⁰Г = 4,02.

15. Искусственный спутник Земли массой m =10³ кг выполнен в виде тонкостенного шара. Для сообщения ему угловой скорости можно использовать магнитное поле Земли, индукция которого равна B = 2⋅10⁻⁵ Тл. Найти угловую скорость ω, которую приобретает спутник при быстрой разрядке аккумуляторов, имеющих заряд q =1,5⋅10⁴ Кл через обмотку N = 20 витков, уложенную на поверхность спутника вдоль окружности большого круга. Считать магнитное поле Земли параллельным плоскости обмотки.

Решение:

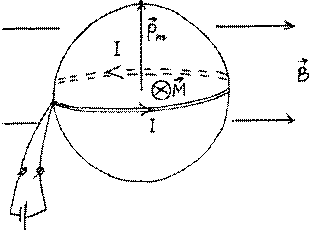При быстром разряде за время ∆t $1 с через обмотку потечет огромный ток I ₌ ^dqdt , создающий в витках обмотки радиуса R (радиус шара) магнитный момент pm = NIS = Ndq Rdtπ 2 .

В магнитном поле _B^! на шар вместе с обмоткой начнет действовать момент сил M _z = p B_m sin90^# ₌ ^{Ndq R Bπ}_dt ² (Угол 90^#, т.к. за малое время ∆t шар не успеет заметно повернуться).

Из уравнения динамики: M z = dLdtz = Iсферы ddtω = 32 mR2 ddtω = Ndq R Bπdt 2                                                                                                                                                                                                                    .

Отсюда ^ω∫0 dω= ^∫0^{q 3π}₂^NB_m dq, получаем  рад/с.

Ответ:  рад/с.

Сила, действующая на постоянные магниты (витки с током):

16. Небольшой магнит с магнитным моментом p_m расположен на оси кругового витка радиуса R с током I . На каком расстоянии l от центра витка должен находиться магнит, чтобы на него действовала максимальная сила притяжения и чему равна эта сила?