Магнитное поле в вакууме. Основные определения и формулы. Магнитное поле равномерно движущегося заряда, страница 2

Ответ: B₀ = ^{µ I} .

Закон Био  Савара  Лапласа:

2. Найти индукцию B в центре квадратной рамки со стороной a, сделанной из тонкого провода, по которому течет ток I .

Решение:

 

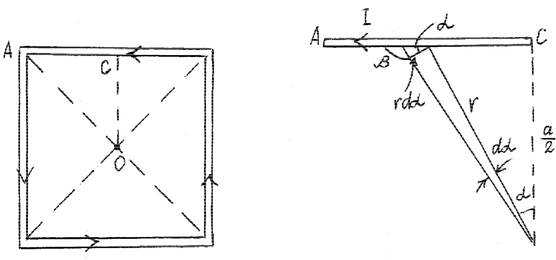
Все стороны квадрата дают одинаковый вклад в магнитную индукцию, т.е. достаточно рассчитать индукцию, создаваемую участком AC = ^a₂ , B = 8B_AC .

B_AC , слишком много переменных (dl r, , β), надо выразить их через одну переменную, например, угол α: r = _cos^{a 2}_α, dl = _cos^rd_α = _2cos^d _α, sinβ = sin(180^# −(90^# −α))= cosα, т.е.

                     π                                                                                                      ππ

BAC = µ0 ∫04 ad2α αcoscos2α(⋅acos2)22α = 4µπ0 a2 ∫04 cosααd   = 2µπ0Ia sinα04 = µ40πI a2 .

4π

Тогда B = 8BAC = 2 2πaµ0I .

Ответ: B = 2 2πaµ0I .

3.  Тонкий провод с изоляцией образует плоскую спираль из большого числа N плотно расположенных витков, по которым течет постоянный ток I . Радиусы внутреннего и внешнего витков равны a и b . Найти магнитную индукцию B в центре спирали.

Решение:

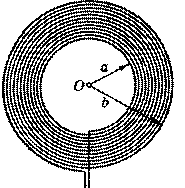Выбираем тонкое кольцо на спирали радиусом r и толщиной dr . В нем расположено dN = _b^N_−a dr витков, т.е. по кольцу течет суммарный ток dI = I dN⋅ = _b^IN_−a dr , создающий в центре спирали индукцию dB = ^µ0₂^⋅_r^dI .

Суммарная индукция B = ∫ba µ2r b0 IN−a dr = 2µ(b0IN−a)ln ab .

Ответ: B = 2µ(b0IN−a)ln ba .

4. 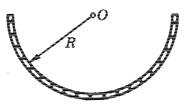 Ток I течет по тонкому прямому проводнику, имеющему форму желоба с поперечным сечением в виде тонкого полукольца радиусом R . Найти магнитную индукцию B на оси О.

Решение:

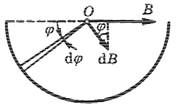Прежде всего, выясним, куда направлен вектор _B^! в точке О. Для этого, мысленно разобьем весь проводник на элементарные нити с током dI . Тогда, ясно, что любые две симметричные нити дадут в сумме  вектор _dB^!, направленный вправо. Значит, туда же будет направлен и вектор _B^! .

Поэтому для нахождения поля _B^! в точке О достаточно найти сумму проекций элементарных векторов _dB^! от каждой нити тока на направление вектора B^! : B = ∫dBsinϕ, dB = ^µdI , где dI = _π^I dϕ, в итоге получим

B = 2µπ02IR π∫0 sinϕϕd       = πµ20RI .

Ответ: B = πµ20RI .

5. Соленоид длины b = 20 см имеет равномерно намотанные витки радиуса R = 10 см, по которым течет постоянный ток. Во сколько раз индукция поля в центре соленоида больше индукции поля на его краю?

Решение:

 

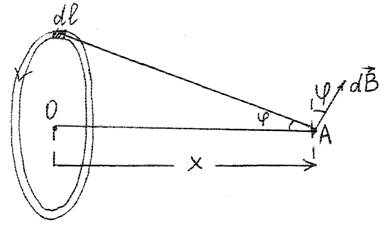
Пусть ток течет по кольцу радиуса R . Элемент тока длины dl создает в точке А на оси кольца магнитное поле с индукцией dB ₌ ^µ0₄^{I dl r}_π^[_r3^{, ]}.

Результирующее поле, созданное всем кольцом в точке А, будет направлено вдоль его оси: B_кольца = ∫dBsinϕ, где sinϕ= ^R_r , r = x² + R² , x  расстояние до центра кольца О. Интегрируя, получаем

B_кольца 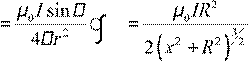dl (1).

Разобьем теперь соленоид на узкие кольца толщины dx, где x  расстояние от центра кольца до центра соленоида О. Такое кольцо содержит dN = _N ^dx_b витков, т.е. по кольцу течет ток dI = IdN ₌ ^INdx_b . В центре соленоида О кольцо создает поле, определяемое выражением (1). Суммируя вклады всех колец, т.е. взяв интеграл вдоль всей длины соленоида, получим

BO x b= 2 µdI R⋅ 2 µ NI . x=−_{b 2} 2(x² + R² ) ² 2 R +b 4

При интегрировании была использована формула ∫(x₂ +^dxR₂ )3₂ = _R2  _x^x_{2 + R}2 .

В точке С на краю соленоида поле вычисляется аналогично, меняется только расстояние от выделенного кольца, поэтому

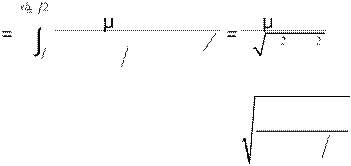_BC       0dI R⋅     ²                  3                  0^NI       . x=−b 2 2((x +b 2)2 + R2 ) 2         2 R +b

В результате находим B_BOC = ₍(_RR2 2₊+_bb2 2₄)₎ ≈1,58.

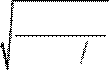Ответ: BBOC = ((_RR2 2++_bb2 2₄)) ≈1,58.

Теорема о циркуляции:

6. На тонкий тороид (баранку) из немагнитного материала равномерно намотана катушка из N =3140 витков. Найти отношение индукции магнитного поля на оси такой катушки к индукции в центре тороида О, если по катушке пропускают постоянный ток.

Решение: