Решение:
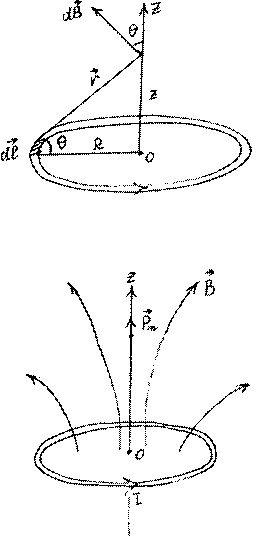 Вначале ищем индукцию поля B! на оси dl r!, ! !
Вначале ищем индукцию поля B! на оси dl r!, ! !
(совпадает с осью z ): dB = µ4π0I r3 (угол
 dB! =
µ4π0I dlsin90r2 #
dB! =
µ4π0I dlsin90r2 #
между dl! и r! всегда равен 90#). Полное поле B! витка направлено вдоль оси 0z , т.е. надо складывать компоненты dBz = dBcosθ:
B ![]() B dB
B dB ![]() dl .
dl .
 Т.к. ∫dl = 2πR, r2 =
R2 +
z2 и cosθ = R2R+
z2 , получаем Bz = 2π µR2 0I 3 =
µ0IR2 3 . 4π(R2 +
z2 )
2 2(R2 +
z2 )
2 Энергия
взаимодействия p!m и B! :
Т.к. ∫dl = 2πR, r2 =
R2 +
z2 и cosθ = R2R+
z2 , получаем Bz = 2π µR2 0I 3 =
µ0IR2 3 . 4π(R2 +
z2 )
2 2(R2 +
z2 )
2 Энергия
взаимодействия p!m и B! :
W = −p B!m ! = −p Bm z ( p!m повернется вдоль оси z ).
![]() Сила
F =
−gradW =
p!m (∇! !B) =
pm ∂∂Bzz e!z очевидно эта сила
направлена против оси 0z
(Fz < 0).
Сила
F =
−gradW =
p!m (∇! !B) =
pm ∂∂Bzz e!z очевидно эта сила
направлена против оси 0z
(Fz < 0).
или R2 +l2 −5l2 = 0: l = R2 .
3 µ0 p IRm 2 R
![]()
![]() На этом расстоянии
Fmax = 2 5 R2 522 = 25 524 µ0Rp I2m .
На этом расстоянии
Fmax = 2 5 R2 522 = 25 524 µ0Rp I2m .
![]() Ответ:
Fmax = 25 524 µ0Rp I2m .
Ответ:
Fmax = 25 524 µ0Rp I2m .
Работа по перемещению контура с током:
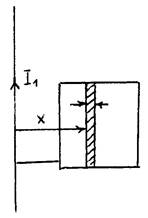
 17. Вблизи длинного провода, по которому течет ток I1 =10 А, расположена квадратная рамка
(см. рис.) с протекающим по ней током I2 =1 А. Рамка и провод лежат в одной плоскости, сторона рамки a = 6,8 см, расстояние b = 4 см. Какую работу надо совершить,
чтобы передвинуть прямой провод в положение, указанное штриховой линией.
17. Вблизи длинного провода, по которому течет ток I1 =10 А, расположена квадратная рамка
(см. рис.) с протекающим по ней током I2 =1 А. Рамка и провод лежат в одной плоскости, сторона рамки a = 6,8 см, расстояние b = 4 см. Какую работу надо совершить,
чтобы передвинуть прямой провод в положение, указанное штриховой линией.
Решение:
 A =
I2∆Φ1, где Φ1 поток магнитной индукции
через площадь рамки, созданный током I1.
A =
I2∆Φ1, где Φ1 поток магнитной индукции
через площадь рамки, созданный током I1.
![]() Вначале
Φ1нач =
∫dΦ =1 ∫BdS1 ,
dS =
adx, B1 =
µ2π0Ix1 , подставив в
Вначале
Φ1нач =
∫dΦ =1 ∫BdS1 ,
dS =
adx, B1 =
µ2π0Ix1 , подставив в
Φ1нач получим ![]() b
b ![]() 2π ab b .
2π ab b .
Если провод перенести в штрихованное положение, то рамка окажется по отношению к нему симметрично с другой стороны, изменится знак B!1 и
![]()
![]() знак Φ1: Φ1кон =
−Φ1нач , т.е.
∆Φ
= Φ1 1кон −Φ1нач =
µ0πI a1 ln a +b b .
знак Φ1: Φ1кон =
−Φ1нач , т.е.
∆Φ
= Φ1 1кон −Φ1нач =
µ0πI a1 ln a +b b .
Тогда работа A![]() Дж.
Дж.
Ответ: ![]() Дж.
Дж.
18. Маленький соленоид с током, обладающий магнитным моментом pm , находится в центре кругового витка радиуса R с током I . Соленоид перемещают вдоль оси витка на расстояние l так, что его ось все время параллельна оси витка. Определить совершенную при этом работу.
20
Решение:
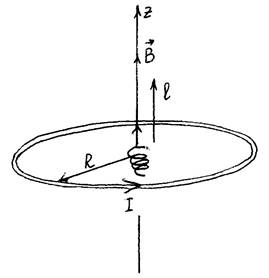 Пусть соленоид состоит из N витков и по нему течет ток Ic , т.е. pm =
NSIc , где S площадь витка соленоида.
Пусть соленоид состоит из N витков и по нему течет ток Ic , т.е. pm =
NSIc , где S площадь витка соленоида.
![]() Тогда
A =
Ic∆Φ,
где Φ
= B NSz поток,
создаваемый током I
в N витках соленоида.
Но в центре большого витка Bz′
=
µ20RI , а на
Тогда
A =
Ic∆Φ,
где Φ
= B NSz поток,
создаваемый током I
в N витках соленоида.
Но в центре большого витка Bz′
=
µ20RI , а на
![]() расстоянии
l по его оси Bz′′
=
µ0IR2 3 (см.
расстоянии
l по его оси Bz′′
=
µ0IR2 3 (см.
2(R2 +l2 ) 2
задачу 16).
![]() Т.е.
A =
I NS Bc ( z′ − Bz′′)=
pm (Bz′ − Bz′′)=
µ20IpRm 1− (1+l21R2 )32 .
Т.е.
A =
I NS Bc ( z′ − Bz′′)=
pm (Bz′ − Bz′′)=
µ20IpRm 1− (1+l21R2 )32 .
Этот результат можно получить и другим способом:
A =W′′−W′ = −p B!m !′′+ p B!m !′.
![]() Ответ:
A =
µ20IpRm 1− (1+l21R2 )32 .
Ответ:
A =
µ20IpRm 1− (1+l21R2 )32 .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.