МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
Если в магнитное поле ввести то или иное вещество, поле изменится, т.к. каждое вещество является магнетиком, т.е. способно под действием магнитного поля намагничиваться (приобретать магнитный момент).
B! = B!0 + B!′, где B!0 первичное поле, B!′
поле, которое создает вещество. При наличии магнетика справедлива теорема Гаусса:
"∫
BdS! ! =
0, т.е. линии вектора
B!
и при наличии вещества остаются всюду непрерывными. Намагниченность: ![]() m , где ∆V физически бесконечно малый
объем в окрестности данной точки, p!m магнитный момент отдельной
молекулы.
m , где ∆V физически бесконечно малый
объем в окрестности данной точки, p!m магнитный момент отдельной
молекулы.
![]()
![]() J! =
n p!m , где n концентрация молекул, p!m средний магнитный
момент одной молекулы.
J! =
n p!m , где n концентрация молекул, p!m средний магнитный
момент одной молекулы.
Молекулярные токи элементарные токи, связанные с каждой молекулой.
Токи намагничивания I′
Токи проводимости I токи, текущие по проводникам, и связанные с перемещением в веществе носителей тока.
![]() Циркуляция
вектора J!:
Для стационарного случая циркуляция намагниченности J!
по произвольному контуру Γ равна алгебраической сумме токов
намагничивания I′,
охватываемых контуром Γ : "∫
Jdl! ! =
I′
, где I′
= ∫
!jdS!,
интегрирование проводится по произвольной поверхности,
Циркуляция
вектора J!:
Для стационарного случая циркуляция намагниченности J!
по произвольному контуру Γ равна алгебраической сумме токов
намагничивания I′,
охватываемых контуром Γ : "∫
Jdl! ! =
I′
, где I′
= ∫
!jdS!,
интегрирование проводится по произвольной поверхности,
«натянутой» на контур Γ .
∇×! !J = !j′ дифференциальная форма уравнения циркуляции вектора J!: ротор намагниченности J! равен плотности тока намагниченности в той же точке пространства.
Вектор H! :
Теорема о циркуляции вектора H! (для магнитного поля постоянных токов): Циркуляция вектора H! по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром: "∫ Hdl! ! = I .
∇×! H! = !j дифференциальная форма теоремы о циркуляции вектора H! , т.е. ротор вектора H! равен плотности тока проводимости в той же точке вещества.
Связь между векторами J! и H! :
J! = χH! , где χ - магнитная восприимчивость.
Для парамагнетиков χ> 0, J! ↑↑ H! , для диамагнетиков χ< 0, J! ↑↓ H! , для ферромагнетиков зависимость J H! !( ) нелинейная, а также наблюдается гистерезис, т.е. зависимость J! от предыстории магнетика.
![]() Связь между
:
Связь между
:
B! = µµ0H! , где µ≡ +1 χ магнитная проницаемость среды.
Парамагнетики: µ> 1, диамагнетики: µ< 1.
Ферромагнетики твердые вещества, которые могут обладать спонтанной намагниченностью, т.е. намагничены уже при отсутствии внешнего магнитного поля.
В единице объема ферромагнетика выделяется теплота Qед, численно равная «площади» петли гистерезиса: Qед = "∫ HdB = Sn .
Температура или точка Кюри температура при которой ферромагнитные свойства исчезают (температура ферромагнитно - парамагнитного перехода).
Магнитная индукция:
1. По оси длинного полого цилиндра натянута нить, заряженная равномерно с линейной плотностью λ. Цилиндр вращается вокруг своей оси с угловой скоростью ω. Определить индукцию магнитного поля в материале цилиндра, вне его и внутри полости (вдали от стенок цилиндра), если цилиндр: 1) металлический и немагнитный; 2) диэлектрический с диэлектрической проницаемостью ε.
Решение:
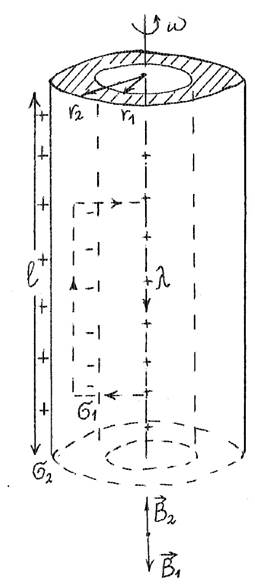 1) цилиндр проводник.
1) цилиндр проводник.
На его внутренней поверхности радиуса r1 и внешней поверхности радиуса r2 появляются индуцированные заряды с плотностью σ1 и σ2 . Величина этих зарядов на всей поверхности совпадает с величиной заряда на нити:
q = −σ π σ π λ1⋅2 rl1 = 2 ⋅2 r l2 = l , где 2πrl1 площадь внутренней поверхности, 2πr l2 площадь внешней поверхности, λl заряд на нити,
т.е.
σ1 = ![]() 2πλr1 , σ2 =
2πλr1 , σ2 = ![]() 2πλr2 , σr =
2πλr2 , σr = ![]() 2λπ .
2λπ .
При вращении цилиндра толщиной dl эти заряды образуют ток
dI ![]() r dl dl
.
r dl dl
.
![]() На
всей длине укладывается N =
dll таких токов.
На
всей длине укладывается N =
dll таких токов.
Т.е. цилиндр, вращаясь, эквивалентен соленоиду по внешним и внутренним «виткам» которого протекают токи dI , но в разных направлениях, т.к. индуцированные заряды σ1 и σ2 имеют противоположный знак.
Поле внутри бесконечно длинного соленоида равно B = µ0dI Nl , а вне
0 при > r r2 вне цилиндра
соленоида равно
нулю, т.е. B =
µ0 ![]() λω2π при < < r1 r r2 в материале цилиндра
λω2π при < < r1 r r2 в материале цилиндра
λω λω
![]() µ0 2π
−µ0 2π
=
0 при < r r1 в полости
µ0 2π
−µ0 2π
=
0 при < r r1 в полости
2) µ=1
По теореме Гаусса для D: D⋅2π λrl = l , где 2πrl площадь цилиндрической
поверхности, λl заряд внутри поверхности;
D =
![]() 2πλr .
2πλr .
![]() Eвнутри =
εε
πεε ε εD0 =
2 λ0 r = ( −P1) 0 . диэлектрика
Eвнутри =
εε
πεε ε εD0 =
2 λ0 r = ( −P1) 0 . диэлектрика
Но P = Pr = Pn =σ′
поверхностный связанный заряд, т.е. на внутренней поверхности плотность связанного
заряда σ1′ =
λε![]() 2(πε−r11), а на
внешней
2(πε−r11), а на
внешней
σ2′ = λωε![]() 2πε(
r−2 1).
2πε(
r−2 1).
dI = σ π′2 rdl = λωε( −1)dl .
![]() 2πω 2πε
2πω 2πε
0 при > r r2 вне цилиндра
![]() B = µ
ε λω0 (
πε−1) при < < r1 r r2 в материале цилиндра
B = µ
ε λω0 (
πε−1) при < < r1 r r2 в материале цилиндра
2
0 при < r r1 в полости
0 при > r r2 вне цилиндра
Ответ: 1) B = µ0 ![]() λω2π при < < r1 r r2 в материале цилиндра
λω2π при < < r1 r r2 в материале цилиндра
λω λω
![]() µ0 2π
−µ0 2π
=
0 при < r r1 в полости
µ0 2π
−µ0 2π
=
0 при < r r1 в полости
0 при > r r2 вне цилиндра
![]() 2)
B =
µ
ε λω0 (
−1) при < < r1 r r2 в материале цилиндра
2)
B =
µ
ε λω0 (
−1) при < < r1 r r2 в материале цилиндра
0 при < r r1 в полости
Циркуляция вектора H! :
2. Прямой длинный тонкий проводник с током I лежит в плоскости, отделяющей пространство, которое заполнено непроводящим магнетиком с проницаемостью µ, от вакуума. Найти магнитную индукцию B во всем пространстве как функцию
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.