Резонансные кривые графики зависимостей от частоты ω внешней ЭДС амплитуд следующих величин: тока I , заряда q на конденсаторе и напряжений UR , UC и UL .
 1
1
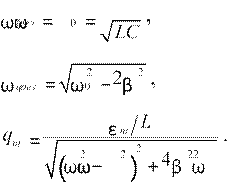
Резонансные частоты для UR , UC и UL : ω ωRрез = 0,
2
 ω
ωCрез =
0 1−2ωβ02 ,
ω
ωCрез =
0 1−2ωβ02 ,
ω0 .
ωLрез = 2
1−2ωβ0
Переменный ток:
![]() Um , ωL− 1
Um , ωL− 1
 U =Um cosωt , I = Im cos(ωt −ϕ),
где Im = 2 +ωL−ω1C 2 tgϕ= RωC . R
U =Um cosωt , I = Im cos(ωt −ϕ),
где Im = 2 +ωL−ω1C 2 tgϕ= RωC . R
2
 Z = R2 +ωL −ω1C
полное сопротивление или импеданс.
Z = R2 +ωL −ω1C
полное сопротивление или импеданс.
X =ωL−ω1C реактивное сопротивление.
X L =ωL индуктивное сопротивление.
XC =ω1C емкостное сопротивление.
![]()
![]() I = Im 2 , U =Um 2 действующие или эффективные
значения тока и напряжения.
I = Im 2 , U =Um 2 действующие или эффективные
значения тока и напряжения.
![]() P =UI cosϕ средняя мощность,
где cosϕ
коэффициент мощности.
P =UI cosϕ средняя мощность,
где cosϕ
коэффициент мощности.
Собственные незатухающие колебания:
1. В контуре, состоящем из конденсатора емкости C и катушки с индуктивностью L, происходят свободные незатухающие колебания с амплитудой напряжения на конденсаторе Um . Найти ЭДС самоиндукции в катушке в моменты, когда ее магнитная энергия оказывается равной электрической энергии конденсатора.
Решение:
Согласно закону Ома RI = +U εс , где U напряжение на конденсаторе
(U =ϕ ϕ1 − 2). В нашем случае R = 0 , поэтому εс =−U .
Остается найти напряжение U в моменты, когда электрическая энергия конденсатора равна магнитной энергии катушки. При этом условии можно записать: , откуда U = Um . 2
 В результате имеем
εс =
Um .
В результате имеем
εс =
Um .
2
![]() Ответ: εс =
Um .
Ответ: εс =
Um .
2
2. Колебательный контур состоит из катушки с индуктивностью L и незаряженного конденсатора емкости С. Активное сопротивление контура R = 0 . Катушка находится в постоянном магнитном поле так, что полный магнитный поток, пронизывающий ее витки, равен Φ. В момент t = 0 магнитное поле резко выключили. Найти ток в контуре как функцию времени t.
Решение:
При резком выключении внешнего магнитного поля в момент t = 0 появится индукционный ток, но конденсатор будет еще не заряженным.
Поэтому согласно закону Ома RI =− ddtΦ− L dIdt .
В данном случае R = 0 и, значит, Φ+ LI = 0. Отсюда Φ= LI0 , где I0 начальный ток (непосредственно после выключения поля).
После выключения внешнего поля процесс будет описываться уравнением
0 =− −Cq L dIdt (1).
Продифференцировав это уравнение по времени, получим d Idt22 + LC1 = 0. Это уравнение гармонических колебаний, его решение ищем в виде
I = Im cos(ω α0t + ).
Постоянные Im и α находим из начальных условий I ( )0 = I0 , dIdt ( )0 = 0
![]() (второе
условие следует из уравнения (1), т.к. в начальный момент t = 0 конденсатор был не заряжен).
Из этих условий найдем α= 0, Im = I0. В результате I = I0 cosω0t =
(второе
условие следует из уравнения (1), т.к. в начальный момент t = 0 конденсатор был не заряжен).
Из этих условий найдем α= 0, Im = I0. В результате I = I0 cosω0t =![]() ΦL cosω0t, где ω0 =
LC1 .
ΦL cosω0t, где ω0 =
LC1 .
Ответ: I = I0 cosω0t =![]() ΦL cosω0t.
ΦL cosω0t.
Добротность контура:
3.
![]() Колебательный
контур с малым затуханием имеет емкость C и индуктивность L. На поддержание в нем незатухающих гармонических
колебаний с амплитудой напряжения на конденсаторе Um необходимо подводить среднюю мощность P . Найти добротность контура.
Колебательный
контур с малым затуханием имеет емкость C и индуктивность L. На поддержание в нем незатухающих гармонических
колебаний с амплитудой напряжения на конденсаторе Um необходимо подводить среднюю мощность P . Найти добротность контура.
Решение:
![]() Вследствие
малости затухания добротность равна Q
Вследствие
малости затухания добротность равна Q![]() , где W энергия, запасенная в контуре,
δW уменьшение этой энергии
за период колебания T .
W =
CU2 m2 и δW = P T . В нашем случае T ≈T0 =
2π
LC .
, где W энергия, запасенная в контуре,
δW уменьшение этой энергии
за период колебания T .
W =
CU2 m2 и δW = P T . В нашем случае T ≈T0 =
2π
LC .
 Окончательно получим
Q =
2UPm2 CL .
Окончательно получим
Q =
2UPm2 CL .
 Ответ: Q = 2UPm2 CL .
Ответ: Q = 2UPm2 CL .
Затухающие колебания:
4. В колебательном контуре имеется конденсатор емкости C , катушка индуктивностью L, активное сопротивление R и ключ. При разомкнутом ключе конденсатор зарядили, а затем замкнули. Найти отношение напряжения на конденсаторе к его амплитудному значению в начальный момент (сразу после замыкания ключа).
Решение:
Напряжение на конденсаторе будет зависеть от времени так же как заряд, поэтому запишем U =U em −βt cos(ω αt + ).
В начальный момент t = 0 напряжение U ( )0 =Um cosα, где Um амплитуда в этот момент. Нам надо найти U ( )0 , т.е. cosα. Um
Для этого воспользуемся другим начальным условием: в момент t = 0 ток
I = =q! 0. Т.к. q =
CU , то достаточно
продифференцировать первое уравнение по времени и полученное выражение при t = 0 приравнять к нулю. Получим −βcosα ω α−
sin =
0, откуда tgα=−![]() .
.
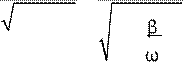 Поэтому
искомое отношение UU(
)m0 =
cosα=
1+1tg2α =
1+1
2 .
Поэтому
искомое отношение UU(
)m0 =
cosα=
1+1tg2α =
1+1
2 .
Принимая во внимание, что ω ω2 = 02 −β2, запишем
 UU(
)m0 = 1−ωβ0 2 = 1− R C42L ,
где учтено, что β= 2RL и ω02 = LC1 .
UU(
)m0 = 1−ωβ0 2 = 1− R C42L ,
где учтено, что β= 2RL и ω02 = LC1 .
Ответ: U ( )0 = 1− R C2 .
Um 4L
5. В колебательном контуре с емкостью C и индуктивностью L совершаются затухающие колебания, при которых ток меняется со временем по закону I t( )= I em −βt sinωt . Найти напряжение на конденсаторе в зависимости от времени.
Решение:
Выберем положительное направление обхода контура контур по часовой стрелке. Согласно закону Ома для участка контура 1RL2 имеем
RI =ϕ ϕ1 − 2 +εc . В нашем случае εc =−LI и ϕ ϕ2 − 1 = Cq =Uc , где q заряд на обкладке 2, поэтому первую формулу можно переписать так: Uc =−RI − LI!. После подстановки сюда выражения для I t( ) и его производной получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.