























Определение.
Пусть ![]() – бесконечная последовательность функций,
определённых на некотором множестве
– бесконечная последовательность функций,
определённых на некотором множестве ![]() . Выражение вида:
. Выражение вида:
![]() (3.1)
(3.1)
называется функциональным рядом и обозначается
сокращённо:  .
.
Пусть число ![]() , тогда ряд:
, тогда ряд:
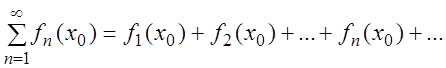 (3.2)
(3.2)
является числовым рядом.
Определение. Если
числовой ряд (3.2) сходится, то ряд (3.1) называется сходящимся в точке х0, а число ![]() называется точкой
сходимости функционального ряда (3.1).
называется точкой
сходимости функционального ряда (3.1).
Определение.
Множество ![]() всех точек сходимости функционального
ряда (3.1) называется его областью сходимости.
всех точек сходимости функционального
ряда (3.1) называется его областью сходимости.
Последнее
определение можно сформулировать иначе: областью сходимости функционального
ряда называется совокупность значений ![]() ,
при которых ряд (3.1) сходится. Как правило, область сходимости
,
при которых ряд (3.1) сходится. Как правило, область сходимости ![]() не совпадает с областью определения
не совпадает с областью определения ![]() функционального ряда, а является её
частью, т.е.
функционального ряда, а является её
частью, т.е. ![]() .
.
Пример 1. Найти область определения и область сходимости функционального ряда:
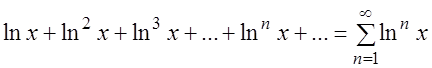 .
.
Решение. Так
как ряд составлен из функций вида ![]() , то их областью
определения является область определения основной элементарной функции
, то их областью
определения является область определения основной элементарной функции ![]() , т.е.
, т.е. ![]() .
Кроме того, данный ряд является суммой членов геометрической прогрессии с
первым членом
.
Кроме того, данный ряд является суммой членов геометрической прогрессии с
первым членом ![]() и знаменателем
и знаменателем ![]() . Такой ряд сходится, если
. Такой ряд сходится, если ![]() , т.е. при
, т.е. при
![]() ,
, 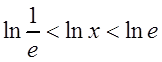 .
.
Поэтому областью сходимости является интервал 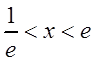 .
.
Таким образом, ![]() и
и 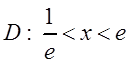 .
Очевидно, что
.
Очевидно, что ![]() .
.
Определение. Как и для числовых рядов, n-й частичной суммой ряда (3.1) называется выражение:
![]() ,
,
а ряд
![]()
называется n-м остатком ряда.
Для любого ![]() из области сходимости
из области сходимости ![]() :
: ![]() и
и
![]() существует.
существует.
Определение.
Функция ![]() , где
, где ![]() ,
называется суммой ряда (3.1). Говорят также, что функция
,
называется суммой ряда (3.1). Говорят также, что функция ![]() , определённая на множестве
, определённая на множестве ![]() , разлагается в функциональный ряд
(3.1) и пишут:
, разлагается в функциональный ряд
(3.1) и пишут:
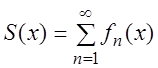
![]() .
.
Если ![]() – сумма ряда,
– сумма ряда, ![]() – n-я частичная сумма ряда
(3.1), то её n-й остаток определяется равенством:
– n-я частичная сумма ряда
(3.1), то её n-й остаток определяется равенством:
![]() .
.
Полезно также другое определение суммы функционального ряда.
Определение.
Функция ![]() называется суммой ряда (3.1) в
некоторой области
называется суммой ряда (3.1) в
некоторой области ![]() , если для любого
, если для любого ![]() существует такой номер
существует такой номер ![]() , что при всех
, что при всех ![]() справедливо неравенство:
справедливо неравенство:
![]()
![]() .
(3.3)
.
(3.3)
В общем случае ![]() зависит от
зависит от ![]() ,
т.е. при заданном
,
т.е. при заданном ![]() натуральные числа
натуральные числа ![]() различны для различных значений
различны для различных значений ![]() . Если же существует один номер
. Если же существует один номер ![]() , такой, что при
, такой, что при ![]() неравенство (3.3) справедливо для
всех
неравенство (3.3) справедливо для
всех ![]() , то ряд (3.1) называется равномерно
сходящимся в D.
, то ряд (3.1) называется равномерно
сходящимся в D.
В случае
равномерной сходимости функционального ряда его n-я частичная сумма является
приближением суммы ряда с одной и той же точностью для всех ![]() .
.
Определение.
Функциональный ряд (3.1) называется мажорируемым в некоторой
области ![]() , если существует сходящийся числовой
ряд:
, если существует сходящийся числовой
ряд:
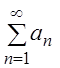
![]() ,
(3.4)
,
(3.4)
такой, что для всех ![]() справедливы
неравенства:
справедливы
неравенства: ![]()
![]() .
.
Ряд (3.4) называется мажорантным (мажорирующим) рядом.
Мажорируемый ряд является рядом равномерно сходящимся.
Например, функциональный ряд:
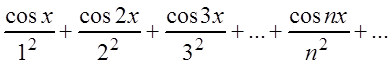
мажорируется рядом 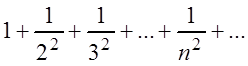 , так как
, так как ![]() .
Данный функциональный ряд равномерно сходится на всей оси
.
Данный функциональный ряд равномерно сходится на всей оси ![]() , поскольку он мажорируется при любом
, поскольку он мажорируется при любом
![]() .
.
Равномерно сходящиеся ряды обладают некоторыми общими свойствами:
1) если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке;
2) если
члены ряда (3.1) непрерывны на отрезке ![]() и
ряд равномерно сходится на этом отрезке, то в случае, когда
и
ряд равномерно сходится на этом отрезке, то в случае, когда ![]() ,
,
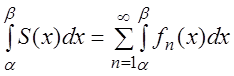 ,
,
где ![]() – сумма ряда (3.1);
– сумма ряда (3.1);
3) если
ряд (3.1), составленный из функций, имеющих непрерывные производные на отрезке ![]() , сходится на этом отрезке к сумме
, сходится на этом отрезке к сумме ![]() и ряд
и ряд
![]()
равномерно сходится на том же
отрезке, то ![]() .
.
Последние два свойства определяют условия, при которых функциональные ряды можно почленно интегрировать и дифференцировать.
Определение. Степенным рядом называется функциональный ряд вида:
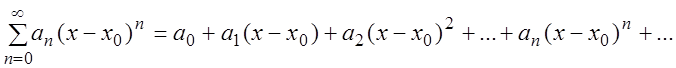 ,
(3.5)
,
(3.5)
где ![]() –
постоянные числа, называемые коэффициентами ряда (3.5),
–
постоянные числа, называемые коэффициентами ряда (3.5), ![]() – фиксированное число.
– фиксированное число.
При ![]() получаем степенной ряд вида:
получаем степенной ряд вида:
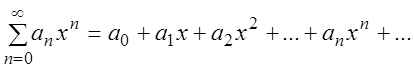 (3.6)
(3.6)
Очевидно, что для (3.5) число ![]() является точкой сходимости.
является точкой сходимости.
Выясним вопрос об области сходимости степенного ряда.
Теорема 3.1 (теорема Абеля)
1) Если
степенной ряд (3.6) сходится при некотором значении ![]() ,
то он абсолютно сходится при всяком значении
,
то он абсолютно сходится при всяком значении ![]() ,
удовлетворяющим условию:
,
удовлетворяющим условию: ![]() .
.
2) Если
степенной ряд (3.5) расходится при некотором значении ![]() ,
то он расходится при любых
,
то он расходится при любых ![]() , для которых
, для которых ![]() .
.
Доказательство
1) Так как по условию числовой ряд 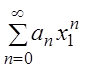 сходится,
то его общий член
сходится,
то его общий член ![]() при
при ![]() , откуда следует, что числовая
последовательность
, откуда следует, что числовая
последовательность
![]()
ограничена, т.е.
существует число ![]() такое, что
такое, что
 ,
, ![]() (3.7)
(3.7)
Перепишем ряд (3.6) в виде:
 (3.8)
(3.8)
и рассмотрим ряд, составленный из абсолютных величин его членов:
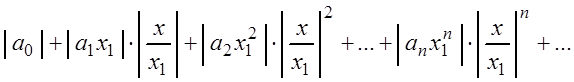 (3.9)
(3.9)
Члены ряда (3.9) в силу неравенства (3.7) меньше соответствующих членов ряда
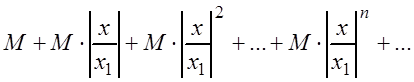 (3.10)
(3.10)
При ![]() ряд (3.10) представляет собой
геометрическую прогрессию со знаменателем
ряд (3.10) представляет собой
геометрическую прогрессию со знаменателем 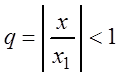 и,
следовательно, сходится. Так как члены ряда (3.9) меньше соответствующих членов
ряда (3.10), то по признаку сравнения (см. теорему 2.3) ряд (3.9) также
сходится, а это значит, что ряд (3.6) при
и,
следовательно, сходится. Так как члены ряда (3.9) меньше соответствующих членов
ряда (3.10), то по признаку сравнения (см. теорему 2.3) ряд (3.9) также
сходится, а это значит, что ряд (3.6) при ![]() сходится
абсолютно (см. теорему 2.8).
сходится
абсолютно (см. теорему 2.8).
2) Докажем
теперь вторую часть теоремы. По условию в точке ![]() ряд
(3.6) расходится. Требуется показать, что он расходится для всех
ряд
(3.6) расходится. Требуется показать, что он расходится для всех ![]() , удовлетворяющих условию:
, удовлетворяющих условию: ![]() . Предположим обратное, т.е.
допустим, что при некотором значении
. Предположим обратное, т.е.
допустим, что при некотором значении ![]() таком, что
таком, что ![]() , ряд (3.6) сходится. Тогда, по
только что доказанной первой части теоремы, ряд (3.6) должен сходится и в точке
, ряд (3.6) сходится. Тогда, по
только что доказанной первой части теоремы, ряд (3.6) должен сходится и в точке
![]() , так как
, так как ![]() .
Но это противоречит тому, что в точке
.
Но это противоречит тому, что в точке ![]() ряд
расходится. Следовательно, ряд расходится и в точке
ряд
расходится. Следовательно, ряд расходится и в точке ![]() .
Таким образом, теорема полностью доказана.
.
Таким образом, теорема полностью доказана.
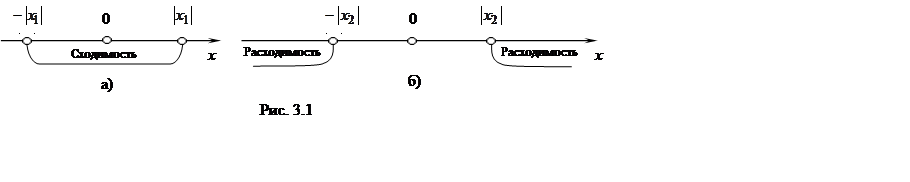
Теорема Абеля
утверждает, что если ![]() – точка сходимости
степенного ряда, то во всех точках, расположенных на интервале
– точка сходимости
степенного ряда, то во всех точках, расположенных на интервале ![]() , этот ряд сходится абсолютно (рис.
3.1,а), а если
, этот ряд сходится абсолютно (рис.
3.1,а), а если ![]() – точка расходимости
степенного ряда (3.6), то во всех точках, расположенных вне интервала
– точка расходимости
степенного ряда (3.6), то во всех точках, расположенных вне интервала ![]() , ряд расходится (рис. 3.1,б).
, ряд расходится (рис. 3.1,б).
Из этого можно заключить, что существует такое число ![]() ,
что при
,
что при ![]() мы имеем точки абсолютной сходимости
и при
мы имеем точки абсолютной сходимости
и при ![]() – точки расходимости.
– точки расходимости.
Таким образом, имеет место следующая теорема о строении области сходимости степенного ряда (3.6).
Теорема 3.2. Областью сходимости степенного ряда (3.6) является интервал с центром в начале координат.
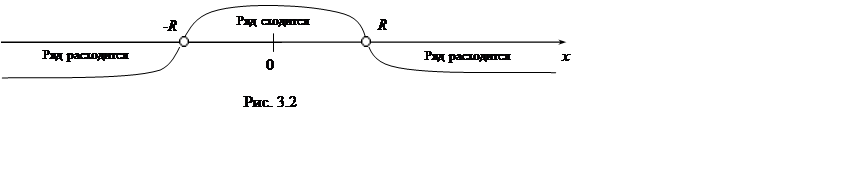
Определение. Неотрицательное число ![]() ,
такое, что при всех
,
такое, что при всех ![]() степенной ряд (3.6)
сходится, а при всех
степенной ряд (3.6)
сходится, а при всех ![]() – расходится, называется радиусом
сходимости степенного ряда (рис. 3.2). Интервал
– расходится, называется радиусом
сходимости степенного ряда (рис. 3.2). Интервал ![]() называется
интервалом сходимости степенного ряда (3.6).
называется
интервалом сходимости степенного ряда (3.6).
На концах
интервала (т.е. при ![]() и при
и при ![]() ) вопрос о сходимости или расходимости
данного ряда решается индивидуально для каждого конкретного ряда.
) вопрос о сходимости или расходимости
данного ряда решается индивидуально для каждого конкретного ряда.
Если ряд (3.6)
сходится только в одной точке ![]() , то для него
радиус сходимости
, то для него
радиус сходимости ![]() . Если ряд (3.6) сходится
для любого действительного числа
. Если ряд (3.6) сходится
для любого действительного числа ![]() , то будем считать,
что
, то будем считать,
что ![]() .
.
Радиус
сходимости степенного ряда обычно находится с использованием признаков Даламбера
и Коши. Рассмотрим способ определения радиуса сходимости ![]() .
.
Рассмотрим ряд, составленный из абсолютных величин членов ряда (3.6):
![]() (3.11)
(3.11)
Так как ряд (3.11) с положительными членами, то для определения его сходимости применим признак Даламбера (см. теорему 3.5).
Допустим, что существует предел:
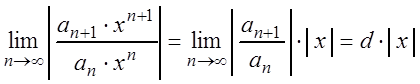 .
.
Тогда по признаку Даламбера ряд
(3.11) сходится, если ![]() , т.е. если
, т.е. если 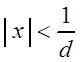 , и расходится, если
, и расходится, если ![]() , т.е. если
, т.е. если 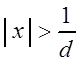 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.