Следовательно,
ряд (3.6) сходится абсолютно при 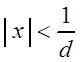 . Если же
. Если же 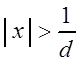 , то ряд (3.11) расходится, причём
его общий член не стремится к нулю (см. теорему 3.5). Но тогда и общий член
данного степенного ряда (3.6) не стремится к нулю, а это значит (на основании
достаточного признака расходимости), что этот степенной ряд расходится (при
, то ряд (3.11) расходится, причём
его общий член не стремится к нулю (см. теорему 3.5). Но тогда и общий член
данного степенного ряда (3.6) не стремится к нулю, а это значит (на основании
достаточного признака расходимости), что этот степенной ряд расходится (при 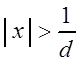 ). Полученный интервал
). Полученный интервал 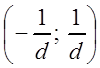 есть интервал сходимости степенного
ряда (3.6), т.е.
есть интервал сходимости степенного
ряда (3.6), т.е.
 .
.
Таким образом, радиус сходимости степенного ряда определяется формулой:
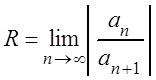 .
(3.12)
.
(3.12)
Аналогичным образом для определения интервала сходимости можно воспользоваться радикальным признаком Коши (см. теорему 3.6), и тогда
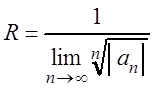 .
(3.13)
.
(3.13)
Рассмотрим степенной ряд (3.5), т.е. ряд вида:
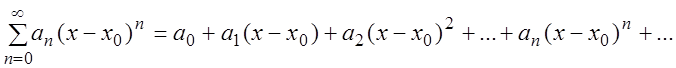
Для определения сходимости этого ряда сделаем замену переменной:
![]() .
.
После этой замены ряд (3.5) имеет вид:
![]() ,
(3.14)
,
(3.14)
т.е. получили степенной ряд вида
(3.6), расположенный по степеням ![]() .
.
Пусть интервал ![]() есть интервал сходимости ряда
(3.14). Отсюда следует, что ряд (3.5) будет сходиться при значениях
есть интервал сходимости ряда
(3.14). Отсюда следует, что ряд (3.5) будет сходиться при значениях ![]() , удовлетворяющих неравенству:
, удовлетворяющих неравенству: ![]() или
или ![]() ,
и будет расходиться вне этого интервала.
,
и будет расходиться вне этого интервала.
Таким образом,
интервал сходимости степенного ряда (3.5) есть интервал с центром в точке ![]() и радиуса
и радиуса ![]() ,
т.е. интервал
,
т.е. интервал ![]() , причём радиус сходимости
, причём радиус сходимости ![]() ряда определяется также по формуле
(3.12) или по формуле (3.13).
ряда определяется также по формуле
(3.12) или по формуле (3.13).
Замечание:
для нахождения области сходимости степенного ряда (3.6) необходимо сначала
определить радиус сходимости, используя формулы (3.12) или (3.13). Если ![]() – конечное число,
– конечное число, ![]() , то для нахождения области
сходимости степенного ряда (3.6), кроме нахождения интервала сходимости,
необходимо исследовать сходимость ряда (3.6) на концах этого интервала, т.е. в
точках
, то для нахождения области
сходимости степенного ряда (3.6), кроме нахождения интервала сходимости,
необходимо исследовать сходимость ряда (3.6) на концах этого интервала, т.е. в
точках ![]() и
и ![]() ,
и присоединить к интервалу
,
и присоединить к интервалу ![]() , тот конец, в
котором ряд (3.6) сходится. Таким образом, областью сходимости ряда (3.6) будет
один из промежутков:
, тот конец, в
котором ряд (3.6) сходится. Таким образом, областью сходимости ряда (3.6) будет
один из промежутков: ![]() ,
, ![]() ,
,
![]() или
или ![]() .
Если
.
Если ![]() , то область сходимости состоит из
одной точки
, то область сходимости состоит из
одной точки ![]() . Если
. Если ![]() ,
то областью сходимости будет вся числовая ось
,
то областью сходимости будет вся числовая ось ![]() .
.
Пример 2.
Найти область сходимости степенного ряда 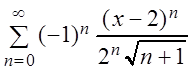 .
.
Решение. Найдём радиус сходимости ряда по формуле (3.12). Так как
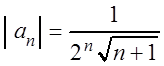 ,
, 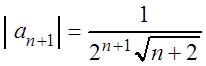 ,
,
то 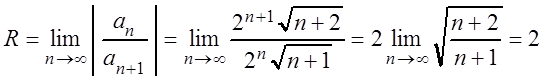 .
.
Определим интервал сходимости ряда. Так как ![]() , то интервал сходимости
, то интервал сходимости ![]() или
или ![]() .
На концах этого интервала ряд может сходиться или расходиться.
.
На концах этого интервала ряд может сходиться или расходиться.
При ![]() получаем ряд:
получаем ряд:
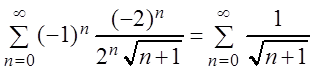 ,
,
который расходится, так как его члены больше членов расходящегося гармонического ряда.
При ![]() получаем
знакочередующийся ряд:
получаем
знакочередующийся ряд:
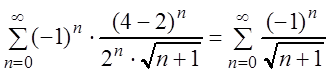 ,
,
члены которого по абсолютной
величине убывают и 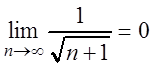 . Следовательно,
знакочередующийся ряд сходится (по признаку Лейбница), причём сходится условно,
так как соответствующий знакоположительный ряд
. Следовательно,
знакочередующийся ряд сходится (по признаку Лейбница), причём сходится условно,
так как соответствующий знакоположительный ряд  расходится.
расходится.
Таким образом, область сходимости данного ряда: (0, 4].
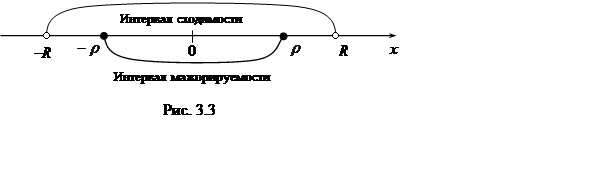
Теорема 3.3. Степенной ряд:
![]() (3.15)
(3.15)
мажорируем
на любом отрезке ![]() , целиком лежащем внутри
интервала сходимости.
, целиком лежащем внутри
интервала сходимости.
Доказательство.
По условию ![]() , а поэтому числовой ряд (с
положительными членами):
, а поэтому числовой ряд (с
положительными членами):
![]() (3.16)
(3.16)
сходится.
Но при ![]() члены ряда (3.15) по абсолютной
величине не больше соответствующих членов ряда (3.16). Следовательно, по определению
ряд (3.15) мажорируем на отрезке
члены ряда (3.15) по абсолютной
величине не больше соответствующих членов ряда (3.16). Следовательно, по определению
ряд (3.15) мажорируем на отрезке![]() (рис. 3.3).
(рис. 3.3).
Следствие 1. На всяком отрезке, целиком лежащем внутри интервала сходимости,
сумма степенного ряда S(x) есть непрерывная функция.
Следствие 2.
Если пределы интегрирования ![]() лежат внутри
интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме
интегралов от членов ряда (т.е. если
лежат внутри
интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме
интегралов от членов ряда (т.е. если ![]() , то ряд можно
почленно интегрировать):
, то ряд можно
почленно интегрировать):
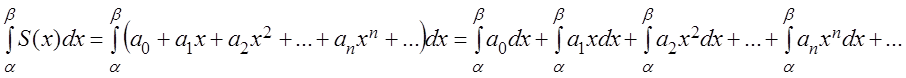
Представляет
интерес интегрирование степенного ряда (3.15) по отрезку ![]() , где
, где ![]() :
:
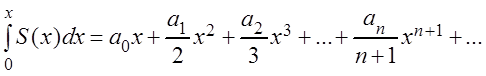
В этом случае опять получаем степенной ряд, который имеет тот же интервал сходимости, что и ряд (3.15).
Следствие 3. Если степенной ряд сходится в интервале (–R, R), то его сумма S(x) представляет собой функцию, имеющую внутри интервала сходимости производные любого порядка. Каждая производная есть сумма ряда, получающегося в результате почленного дифференцирования данного ряда (3.15) соответствующее число раз; при этом интервал сходимости каждого ряда, получившегося в результате дифференцирования, есть тот же интервал (–R, R), т.е.
![]() ,
,
![]() , …, если
, …, если ![]() .
.
Пусть функция S(x)
является суммой степенного ряда:  на интервале сходимости
на интервале сходимости
![]() , другими словами, S(x)
разлагается в степенной ряд:
, другими словами, S(x)
разлагается в степенной ряд:
![]() (3.17)
(3.17)
Так как ряд
(3.17) приводится к виду (3.15) заменой переменной ![]() ,
то функция S(x) обладает следующими свойствами:
,
то функция S(x) обладает следующими свойствами:
1) функция S(x)
непрерывна на интервале ![]() ;
;
2) степенной ряд (3.17) можно почленно дифференцировать в любой точке интервала сходимости, т.е.
![]() ,
,
а это означает, что функция S(x) в интервале сходимости дифференцируема бесконечное число раз;
3) степенной ряд
(3.17) можно почленно интегрировать по любому отрезку ![]() ,
если
,
если ![]() , причем
, причем
 .
.
Теорема 3.4.
Если функция ![]() на интервале
на интервале ![]() разлагается
в степенной ряд:
разлагается
в степенной ряд:
![]() ,
(3.18)
,
(3.18)
то это разложение единственно.
Доказательство.
По условию ряд (3.18) сходится на интервале ![]() ,
и функция
,
и функция ![]() – его сумма. Следовательно, на
основании второго свойства, ряд (3.18) можно почленно дифференцировать на
интервале
– его сумма. Следовательно, на
основании второго свойства, ряд (3.18) можно почленно дифференцировать на
интервале ![]() любое число раз. Дифференцируя, получаем:
любое число раз. Дифференцируя, получаем:
![]()
![]() ,
,
![]() ,
,
……………………………………………………………………………………...
![]() , …
, …
Полагая в полученных равенствах и в равенстве (3.18) ![]() , имеем:
, имеем:
![]() ,
, ![]() ,
,
![]() , …,
, …, ![]() ,
…
,
…
откуда находим:
![]() ,
,
 ,
, 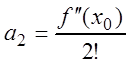 ,
…,
,
…, 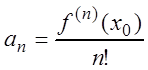 , … (3.19)
, … (3.19)
Таким образом, все коэффициенты ряда (3.18) определяются единственным образом формулами (3.19), что и доказывает теорему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.