Для каждого
случая в скобках указана область, в которой степенной ряд сходится к
соответствующей функции. Последний ряд, называемый биноминальным,
на концах интервала сходимости ведёт себя по-разному в зависимости от ![]() : при
: при ![]() абсолютно
сходится в точках
абсолютно
сходится в точках ![]() ; при
; при ![]() расходится в точке
расходится в точке ![]() и условно сходится в точке
и условно сходится в точке ![]() ; при
; при ![]() расходится
в точках
расходится
в точках ![]() .
.
Рассмотрим наиболее важные применения степенных рядов.
Вычисление приближённого значения функции
Для нахождения
приближённого значения функции ![]() с заданной
точностью
с заданной
точностью ![]()
![]() ,
сначала разлагают функцию
,
сначала разлагают функцию ![]() в степенной ряд и
полагают в нём
в степенной ряд и
полагают в нём ![]() . Затем устанавливают,
сколько первых членов полученного числового ряда надо взять, чтобы их сумма
была приближённым значением
. Затем устанавливают,
сколько первых членов полученного числового ряда надо взять, чтобы их сумма
была приближённым значением ![]() с заданной
точностью
с заданной
точностью ![]() , т.е.
, т.е. ![]() .
В результате, получают:
.
В результате, получают: ![]() .
.
Пример 1. Вычислить с точностью до 0,001 значение 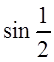 .
.
Решение. В ряде Маклорена (3.32) для ![]() положим
положим
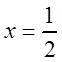 , это можно сделать, так как
равенство (3.32) справедливо для любого
, это можно сделать, так как
равенство (3.32) справедливо для любого ![]() ,
в результате получим:
,
в результате получим:
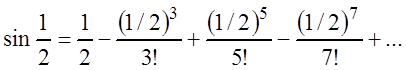
Необходимо найти ![]() , при котором
, при котором 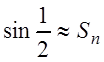 , и ошибка была бы не больше, чем
требуемая в задаче точность
, и ошибка была бы не больше, чем
требуемая в задаче точность ![]() .
.
Ряд
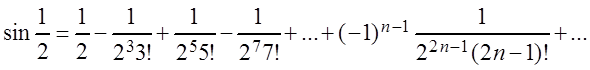
является знакочередующимся, поэтому по следствию из признака Лейбница
![]() .
.
Так как
![]() ,
, 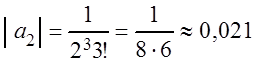 ,
,
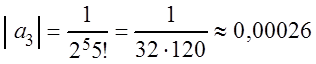 ,
,
т.е. уже третий
член ряда меньше ![]() , то
, то ![]() , и с точностью до 0,001
, и с точностью до 0,001
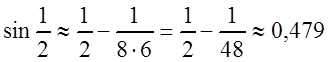 .
.
Пример 2. Вычислить ![]() с точностью
с точностью ![]() .
.
Решение.
Известно, что степенной ряд (3.34) при ![]() сходится
условно. Для того чтобы вычислить
сходится
условно. Для того чтобы вычислить ![]() с помощью ряда
(3.34) с точностью
с помощью ряда
(3.34) с точностью ![]() , необходимо взять не менее
10 000 его членов. Поэтому воспользуемся рядом, который получается в результате
вычитания степенных рядов функций
, необходимо взять не менее
10 000 его членов. Поэтому воспользуемся рядом, который получается в результате
вычитания степенных рядов функций ![]() и
и ![]() :
:
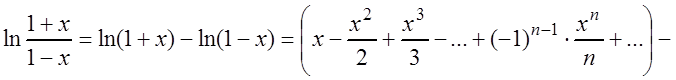
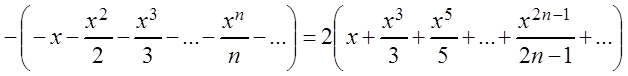 .
.
При ![]() полученный ряд сходится абсолютно.
Поскольку
полученный ряд сходится абсолютно.
Поскольку 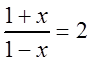 при
при 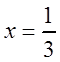 ,
то, подставив это значение
,
то, подставив это значение ![]() в ряд, получим:
в ряд, получим:
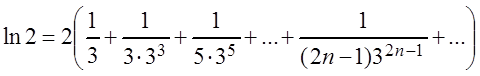 .
.
Для вычисления ![]() с заданной точностью необходимо
найти такое число
с заданной точностью необходимо
найти такое число ![]() членов частичной суммы
членов частичной суммы ![]() , при котором сумма остатка
, при котором сумма остатка ![]() . В нашем случае
. В нашем случае
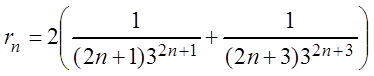 .
(3.39)
.
(3.39)
Поскольку числа
![]() ,
, ![]() ,
… больше, чем
,
… больше, чем ![]() , то, заменив их на
, то, заменив их на ![]() , мы увеличим каждую дробь в формуле
(3.39). Поэтому
, мы увеличим каждую дробь в формуле
(3.39). Поэтому
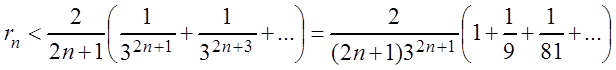 .
.
В скобках
получили сумму бесконечно убывающей геометрической прогрессии: 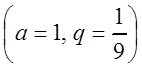 , которая равна
, которая равна 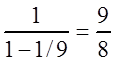 , поэтому
, поэтому 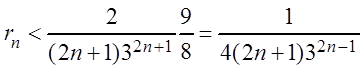 .
.
Путём подбора
значений ![]() находим, что для
находим, что для ![]()
![]() ,
при этом
,
при этом
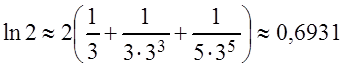 .
.
Вычисление интегралов
Так как степенные ряды можно почленно интегрировать по любому отрезку, лежащему внутри их интервала сходимости, то с помощью разложения подынтегральной функции в степенной ряд можно находить приближённое значение определённого интеграла.
Пример 3. Вычислить
приближённо с точностью до 0,001 определённый интеграл: 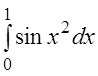 .
.
Решение.
Первообразная функции ![]() не выражается через
элементарные функции, поэтому применим ряд (3.32), в который вместо
не выражается через
элементарные функции, поэтому применим ряд (3.32), в который вместо ![]() подставим
подставим ![]() :
:
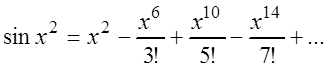 ,
,
который сходится к функции ![]() при любом
при любом ![]() .
Тогда
.
Тогда
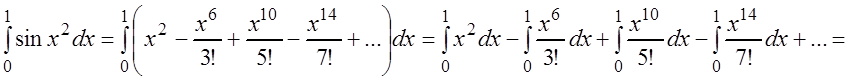
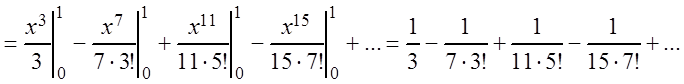 ,
,
т.е.
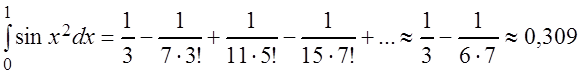 ,
,
так как уже третий член
полученного знакочередующегося ряда меньше ![]() .
.
Приближённое решение дифференциальных уравнений
В случае, когда точно проинтегрировать дифференциальное уравнение не удаётся, его решение удобно искать в виде степенного ряда, например, ряда Тейлора или Маклорена.
При решении задачи Коши
![]() ,
,
![]() ,
(3.40)
,
(3.40)
используется ряд Тейлора:
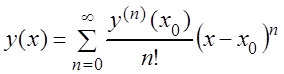 ,
(3.41)
,
(3.41)
где ![]() ,
,
![]() , а остальные производные
, а остальные производные ![]()
![]() находятся
путём последовательного дифференцирования уравнения (3.40) и подстановки
начальных данных в выражения для этих производных.
находятся
путём последовательного дифференцирования уравнения (3.40) и подстановки
начальных данных в выражения для этих производных.
Пример 4.
Дано дифференциальное уравнение: ![]() . Найти частное
решение, удовлетворяющее начальному условию
. Найти частное
решение, удовлетворяющее начальному условию ![]() ,
в виде ряда Тейлора (взяв первые 5 его членов).
,
в виде ряда Тейлора (взяв первые 5 его членов).
Решение. Пусть решением исходного дифференциального уравнения является функция:
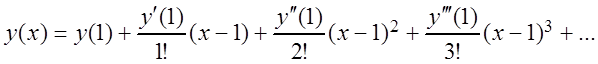 (3.42)
(3.42)
Начальное
условие ![]() даёт первый член этого ряда.
Подставив
даёт первый член этого ряда.
Подставив ![]() и
и ![]() в
данное уравнение
в
данное уравнение ![]() , получим:
, получим: ![]() . Продифференцируем исходное
уравнение по переменной х:
. Продифференцируем исходное
уравнение по переменной х:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
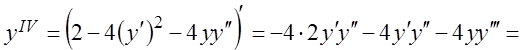
![]() ,
,
![]()
и т.д. Подставим найденные значения в ряд (3.42)
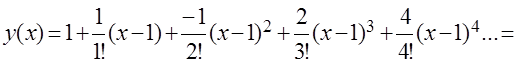
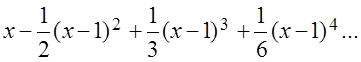
Определение. Функциональный ряд вида:
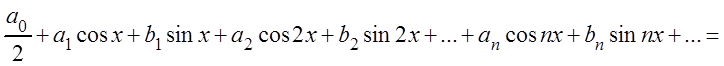
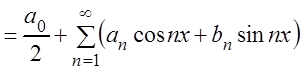 (3.43)
(3.43)
называется тригонометрическим
рядом, а числа: ![]() – коэффициентами
тригонометрического ряда.
– коэффициентами
тригонометрического ряда.
Если ряд (3.43) сходится, то его
сумма есть периодическая функция f(x) с периодом![]() , так как
, так как ![]() и
и
![]() являются периодическими
функциями с периодом
являются периодическими
функциями с периодом ![]() . Таким образом,
. Таким образом,
![]() .
.
Кроме того,
функции ![]() и
и ![]() образуют
систему функций ортогональную на отрезке
образуют
систему функций ортогональную на отрезке ![]() в
следующем смысле: интеграл по отрезку
в
следующем смысле: интеграл по отрезку ![]() от
произведения любых двух различных функций этой системы равен нулю, а интеграл
по отрезку
от
произведения любых двух различных функций этой системы равен нулю, а интеграл
по отрезку ![]() от квадрата любой функции этой
системы отличен от нуля.
от квадрата любой функции этой
системы отличен от нуля.
Действительно,
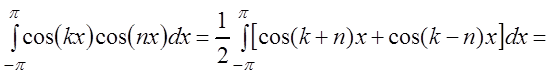
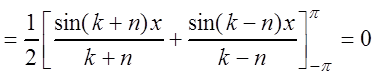 при
при
![]() . (3.44)
. (3.44)
Аналогично находим:
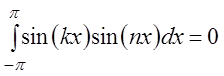 при
при
![]() ;
; 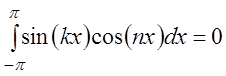 ;
(3.45)
;
(3.45)
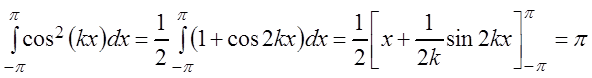 ;
(3.46)
;
(3.46)
|
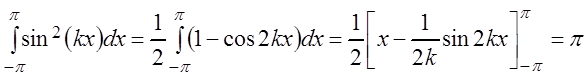 ;
;
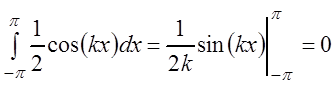 ;
; 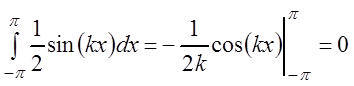 ;
;
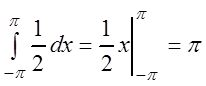 .
(3.48)
.
(3.48)
Тригонометрические ряды особенно удобны при изучении периодических функций, описывающих различные периодические процессы (колебательные и вращательные движения различных деталей машин и приборов, периодическое движение небесных тел и элементарных частиц, акустические и электромагнитные колебания и др.).
Теорема 3.6.
Если функция f(x), определенная и интегрируемая на отрезке ![]() , разлагается в тригонометрический
ряд:
, разлагается в тригонометрический
ряд:
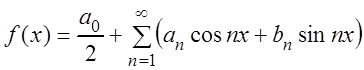 ,
(3.49)
,
(3.49)
который можно интегрировать почленно, то это разложение единственно.
Доказательство. Интегрируя (3.49) и учитывая формулы (3.48), получаем:
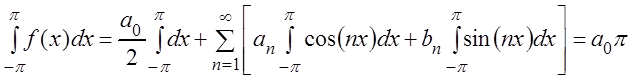 ,
,
откуда находим:
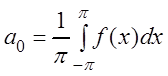 .
(3.50)
.
(3.50)
Для определения
коэффициента ![]() при
при ![]()
![]() умножим равенство (3.49) на
умножим равенство (3.49) на ![]() и проинтегрируем по
и проинтегрируем по ![]() от
от ![]() до
до
![]() (ряд можно интегрировать почленно после
умножения его на ограниченную функцию). Тогда на основании формул (3.44) – (3.48)
получаем:
(ряд можно интегрировать почленно после
умножения его на ограниченную функцию). Тогда на основании формул (3.44) – (3.48)
получаем:
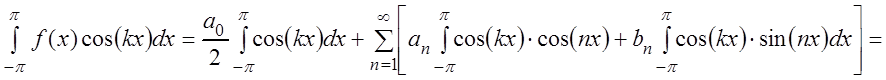
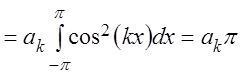 ,
,
откуда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.