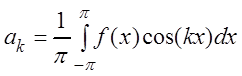 .
(3.51)
.
(3.51)
Аналогично,
умножая равенство (3.49) на ![]() и интегрируя в
пределах от
и интегрируя в
пределах от ![]() до
до ![]() ,
получаем:
,
получаем:
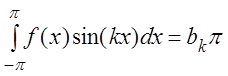 ,
,
откуда
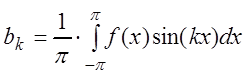 .
(3.52)
.
(3.52)
Таким образом,
коэффициенты ![]() и
и ![]() ряда
(3.49) определяются единственным образом формулами (3.50) – (3.52), что и доказывает
теорему.
ряда
(3.49) определяются единственным образом формулами (3.50) – (3.52), что и доказывает
теорему.
Эта теорема дает основание ввести следующее определение.
Определение. Функциональный ряд вида:
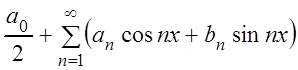 ,
(3.53)
,
(3.53)
где коэффициенты ![]()
![]() определяются
по формулам:
определяются
по формулам:
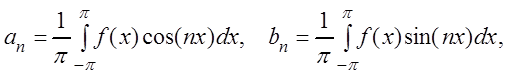 (3.54)
(3.54)
называется рядом Фурье
функции f(x). Отметим, что всегда ![]() .
.
Выясним, какими свойствами должна обладать функция f(x), чтобы построенный для нее ряд Фурье сходился, и чтобы сумма построенного ряда Фурье равнялась значениям данной функции в соответствующих точках.
Определение.
Функция f(x) называется кусочно-монотонной на отрезке [a, b],
если отрезок можно разбить конечным числом точек ![]() на
интервалы
на
интервалы ![]() так, чтобы в каждом из них функция
была монотонна.
так, чтобы в каждом из них функция
была монотонна.
Из
определения следует, что если функция f(x) – кусочно-монотонна и
ограниченная на отрезке [a, b], то она может иметь только точки
разрыва первого рода. Действительно, если ![]() есть
точка разрыва функции f(x), то в силу монотонности функции
существуют пределы:
есть
точка разрыва функции f(x), то в силу монотонности функции
существуют пределы:
![]()
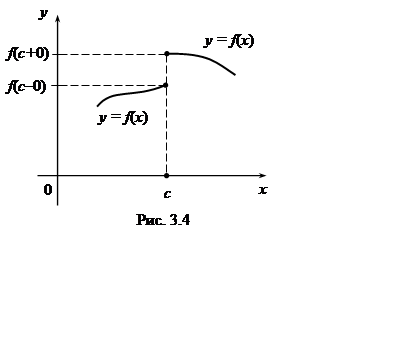
т.е.
точка ![]() есть точка разрыва первого рода
(рис. 3.4).
есть точка разрыва первого рода
(рис. 3.4).
 Сформулируем теорему,
которая дает достаточные условия представимости функции f(x)
рядом Фурье.
Сформулируем теорему,
которая дает достаточные условия представимости функции f(x)
рядом Фурье.
Теорема 3.7.
Если функция f(x) периодическая с периодом ![]() , кусочно-монотонна и ограниченна на
отрезке
, кусочно-монотонна и ограниченна на
отрезке ![]() , то
, то
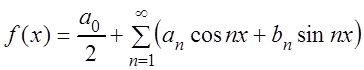
для любой точки непрерывности ![]() (т.е. является суммой своего ряда
Фурье). Если же точка
(т.е. является суммой своего ряда
Фурье). Если же точка ![]() – точка разрыва первого
рода функции
– точка разрыва первого
рода функции ![]() , то сумма
, то сумма ![]() ряда
Фурье в этой точке
ряда
Фурье в этой точке
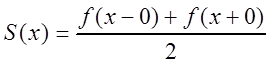 ,
,
где ![]() –
пределы слева и справа соответственно в точке х.
–
пределы слева и справа соответственно в точке х.
Из теоремы
следует, что ![]() в точках непрерывности
функции
в точках непрерывности
функции ![]() и сумма
и сумма ![]() равна
среднему арифметическому пределов слева и справа функции
равна
среднему арифметическому пределов слева и справа функции ![]() в точках разрыва первого рода.
в точках разрыва первого рода.
Из теоремы следует также, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных разделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики.
Пример 1.
Разложить в ряд Фурье функцию ![]() , имеющую период
, имеющую период ![]() и заданную на промежутке
и заданную на промежутке ![]() следующим образом:
следующим образом:
|
|
если |
|
если |
Решение.
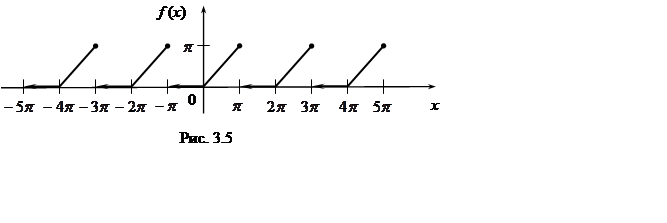
Функция ![]() (рис. 3.5) имеет точки разрыва
(рис. 3.5) имеет точки разрыва ![]() ,
, ![]() .
.
Так как ![]() кусочно-монотонная и имеет на
отрезке
кусочно-монотонная и имеет на
отрезке ![]() лишь одну точку разрыва первого рода
лишь одну точку разрыва первого рода
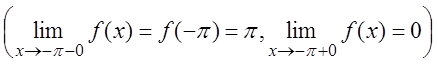 , то во всех точках
, то во всех точках ![]() непрерывности функция
непрерывности функция ![]() разлагается в ряд Фурье. Найдём
коэффициенты ряда по формулам (3.54):
разлагается в ряд Фурье. Найдём
коэффициенты ряда по формулам (3.54):
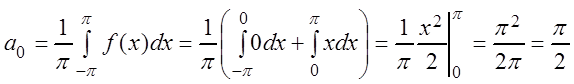 ;
;
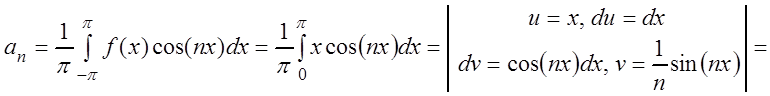
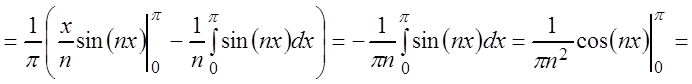
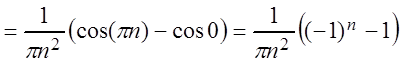 ,
, ![]() ;
;
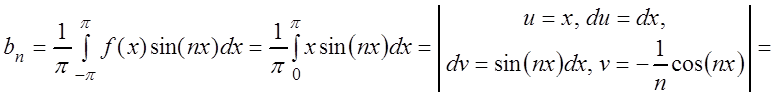
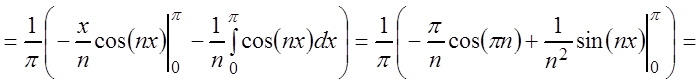
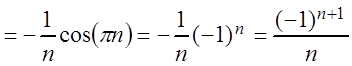 ,
, ![]() .
.
Подставляя найденные коэффициенты в ряд (3.53), получаем:
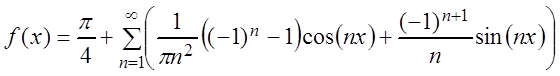 ,
,
для любого![]() ,
,
![]() . В точках сумма найденного ряда
. В точках сумма найденного ряда 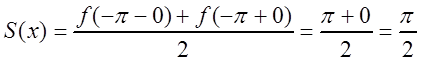 (рис. 3.6).
(рис. 3.6).
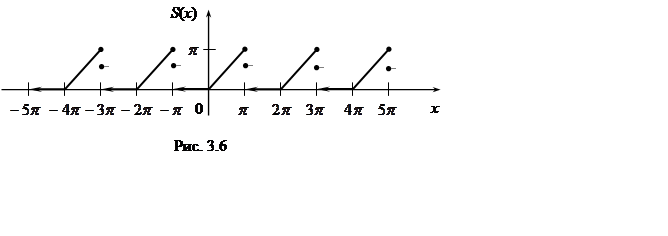
Пусть ![]() есть периодическая функция с
периодом
есть периодическая функция с
периодом ![]() , вообще говоря, отличным от
, вообще говоря, отличным от ![]() . Разложим её в ряд Фурье.
. Разложим её в ряд Фурье.
Сделаем замену
переменной по формуле 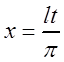 . Тогда функция
. Тогда функция  будет периодической функцией от
будет периодической функцией от ![]() с периодом
с периодом ![]() .
Её можно разложить в ряд Фурье на отрезке
.
Её можно разложить в ряд Фурье на отрезке ![]() :
:
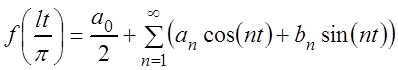 ,
(3.55)
,
(3.55)
где 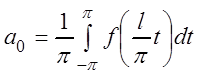 ,
, 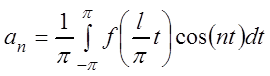 ,
,
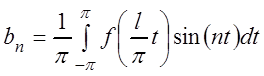 .
.
Возвратимся
теперь к старой переменной ![]() :
:
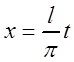 ,
, 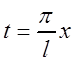 ,
,
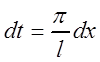 .
.
Тогда
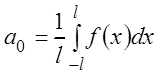 ,
, 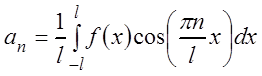 ,
,
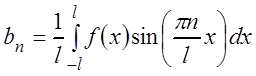 , (3.56)
, (3.56)
где ![]() .
Формула (3.55) получит вид:
.
Формула (3.55) получит вид:
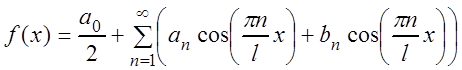 ,
(3.57)
,
(3.57)
где коэффициенты ![]() вычисляются по формулам (3.56). Это
и есть ряд Фурье для периодической функции с периодом 2l.
вычисляются по формулам (3.56). Это
и есть ряд Фурье для периодической функции с периодом 2l.
Теорема 3.8.
Если периодическая функция с периодом ![]() кусочно-монотонная
и ограниченная на отрезке
кусочно-монотонная
и ограниченная на отрезке ![]() , то её ряд Фурье
(3.57) сходится для любого
, то её ряд Фурье
(3.57) сходится для любого ![]() к сумме:
к сумме:
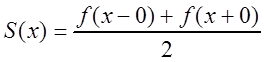 .
.
Нетрудно
видеть, что если периодическая функция чётная, то она разлагается в ряд Фурье
только по косинусам, а если нечётная, то по синусам. Из определения чётной и
нечётной функции следует, что если ![]() – чётная функция,
то
– чётная функция,
то 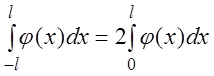 , а если
, а если ![]() –
нечётная функция, то
–
нечётная функция, то 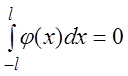 . Таким образом, если в ряд
Фурье разлагается нечётнаяфункция
. Таким образом, если в ряд
Фурье разлагается нечётнаяфункция ![]() ,
то произведение
,
то произведение 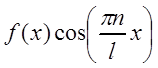 есть функция также
нечётная, а
есть функция также
нечётная, а 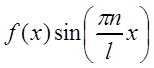 – чётная, следовательно,
– чётная, следовательно,
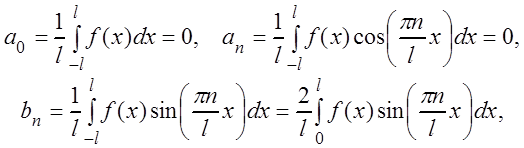 (3.58)
(3.58)
т.е. ряд Фурье нечётной функции содержит «только синусы»:
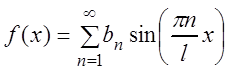 .
(3.59)
.
(3.59)
Если в ряд
Фурье разлагается чётная функция ![]() , то произведение
, то произведение 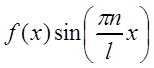 есть функция нечётная,
есть функция нечётная, 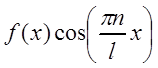 – чётная и, следовательно,
– чётная и, следовательно,
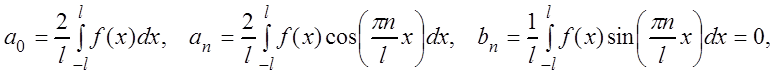 (3.60)
(3.60)
т.е. ряд Фурье чётной функции содержит «только косинусы»:
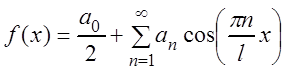 .
(3.61)
.
(3.61)
Полученные формулы позволяют упрощать вычисления при нахождении коэффициентов Фурье в тех случаях, когда заданная функция является чётной или нечётной.
Формулы (3.58)
– (3.61) справедливы и в том случае, когда ![]() –
периодическая функция с периодом
–
периодическая функция с периодом ![]()
![]() .
.
Рассмотрим
разложение в ряд Фурье непериодической функции ![]() .
.
Если функция ![]() определена только на отрезке
определена только на отрезке ![]() , то рассматривают её периодическое
продолжение (с периодом
, то рассматривают её периодическое
продолжение (с периодом ![]() ) на всю числовую
ось и разлагают его в ряд Фурье обычным образом.
) на всю числовую
ось и разлагают его в ряд Фурье обычным образом.
Если функция
задана на отрезке ![]() , то сначала продолжают её
на отрезке
, то сначала продолжают её
на отрезке ![]() чётным или нечётным образом, а затем
периодически продолжают на всю числовую ось.
чётным или нечётным образом, а затем
периодически продолжают на всю числовую ось.
Пример 2.
Разложить в ряд Фурье функцию ![]() , определённую на
отрезке
, определённую на
отрезке ![]() равенством:
равенством: 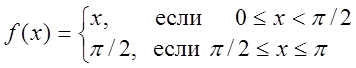 .
.
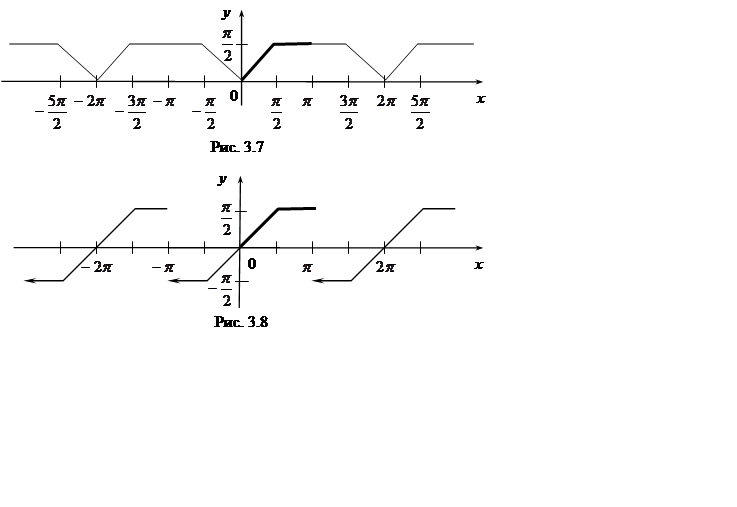
Решение. Функцию ![]() можно продолжить
на отрезке
можно продолжить
на отрезке ![]() либо чётным (рис. 3.7), либо
нечётным (рис. 3.8) образом, а затем рассмотреть её периодическое (с периодом
либо чётным (рис. 3.7), либо
нечётным (рис. 3.8) образом, а затем рассмотреть её периодическое (с периодом ![]() ) продолжение на всю числовую ось.
) продолжение на всю числовую ось.
Чётное
продолжение функции ![]() непрерывно на всей
действительной оси и разлагается в ряд по косинусам, а нечётное продолжение
имеет разрыв первого рода в точках
непрерывно на всей
действительной оси и разлагается в ряд по косинусам, а нечётное продолжение
имеет разрыв первого рода в точках ![]()
![]() и разлагается по синусам.
и разлагается по синусам.
Вычислим
коэффициенты рядов Фурье для этих продолжений по формулам (3.58) и (3.60) при ![]() .
.
Для нечётного
продолжения функции ![]() :
:
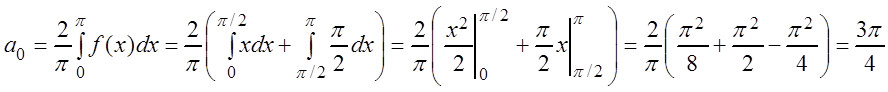 ,
,
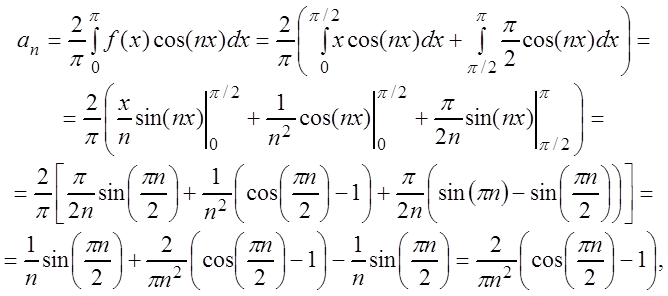
![]() ,
,
тогда
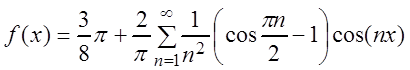
![]() .
.
Для нечётного
продолжения функции ![]() :
:
![]() ,
, ![]() ,
,
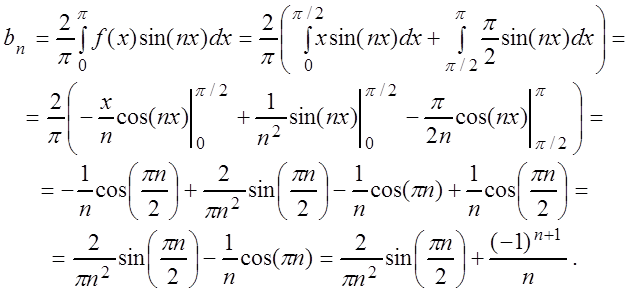
Тогда
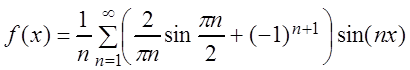
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.