Решение задачи о смеси продукции (производство столов)

3-5. ЗАДАЧА О СМЕСИ ПРОДУКЦИИ

Мебельная компания производит четыре модели письменных столов. Каждый стол сначала изготовляется в столярном цехе, а затем отправ­ляется в отделочный цех, где он лакируется, покрывается воском и поли­руется. Количество рабочих часов, требуемое в каждом цехе, описывается следующей таблицей:

	Стол 1	Стол 2	Стол 3	Стол 4
Столярный цех      (раб.час)	4	9	7	10
Отделочный цех    (раб.час)	1	1	3	40

             Из-за ограничений, налагаемых на мощность завода, в течение ближай­ших шести месяцев можно рассчитывать не более чем на 6000 рабочих часов в столярном цехе и на 4000 рабочих часов в отделочном цехе.

Прибыль (т. е. доход минус производственные расходы) от продажи каждого стола следующая:

Столы	1          2            3            4
Прибыль        (долларов)	12        20          18          40

В предположении, что сырье и оборудование имеются в достаточных коли­чествах и что все изготовленные столы можно продать, компания по про­изводству столов хочет определить оптимальную смесь продукции, т. е. объемы продукции каждого типа, которые в совокупности максимизируют прибыль.

Шаг 1. Технологические процессы. Четыре технологических процесса суть

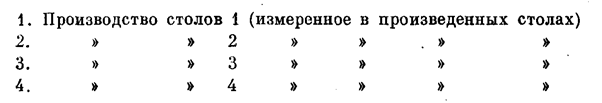
Шаг 2. Ингредиенты.

1. Объем столярных работ (измеренный в человеко-часах).

2. Объем отделочных работ (измеренный в человеко-часах).

3. Стоимость (измеренная в долларах).

Шаг 3. Коэффициенты. Технологический процесс 1, например, может быть изображен на диаграмме следующим образом:

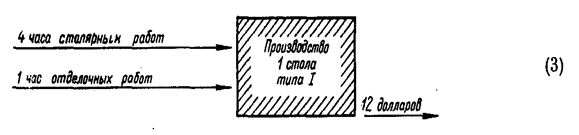
Таблица коэффициентов затрат - выпуска, составленная из (1) и (2), показана на табл. 3-5-1.

Шаг 4. Экзогенные потоки. Так как объемы столярных и отделочных работ являются затратами для каждого из этих технологических процес­сов, они должны быть затратами для системы как целого. Однако мы долж­ны учесть еще и тот факт, что допустимый план не обязательно должен использовать эти объемы полностью. Известно, что общие затраты не должны превышать 6000 часов столярных работ и 4000 часов отделочных работ, но меньше этих предельных объемов они могут быть и поэтому не обязательно должны выражаться точно в виде уравнений материаль­ного баланса.

Таблица 3-5-1

Таблица коэффициентов: задача о смеси продукции

Технологические              Процессы            Ингредиенты :	Производство столов
	(1)          (2)          (3)             (4)
1.  Объем столярных работ                    (в часах)	4              9             7             10
2.      Объем отделочных работ           (в часах)	1                1           3              40
2.  Стоимость (долл.)	-12             -20         -18         - 40

Шаг 5. Материальный баланс. Для сохранения реальности в математической формули­ровке мы должны для материального баланса вместо уравнений написать неравенства, выражающие, например, ограничения, налагаемые на объем столярных работ, в виде неравенства

а отнюдь не в виде уравнения, которое не вполне соответствует нашим условиям.

Мы видим, что модель не может быть завершена построением приве­денных выше списков технологических процессов и ингредиентов, и мы имеем дело со случаем,  когда необхо­дим повторный переход к началу построения модели.

Все, что нам остается теперь сделать,- это добавить к модели тех­нологические процессы, которые учтут столярные и отделочные мощности, неиспользованные в остальной части плана.

Если мы определим в качестве технологического процесса «не ис­пользовать мощность», то получим два дополнительных технологических процесса к тем, которые уже были выписаны на шаге 1.

5. Не использовать мощность столярного цеха (измеренную в человеко-часах).

6. Не использовать мощность отделочного цеха (измеренную в человеко-часах).

Процесс 5 может быть абстрактно изображен следующим образом:

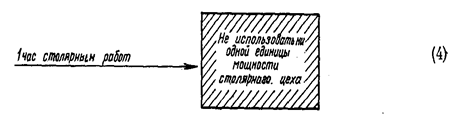
Полная таблица коэффициентов затрат - выпуска и экзогенных возмож­ностей системы как целого показана в табл.

              3-5-11.

Технологические прцессы          Ингредиенты	Производство столов
	х1	х2	х3	х4	х5	Х6
1 Столярные работы      (чел.час.)           в столярн.цехе	4	9	7	10
2 Отделочные работы    (чел.час.)    в отделочном цехе	1	1	3	40
3 Прибыль от продажи столов   (долларов)	-12	-20	-18	-40
4 Неиспользуемый ресурс столярного цеха					1
5 Неиспользуемый ресурс отделочного цеха						1

Пример1 решает поставленную задачу в области вещественных решений и в предположении возможности незавершенного производства.

Ниже приводится теоретическое решение этой-же задачи. При этом вводятся новые переменные .

Соотношения между старой и новой интенсивностями технологических   про­цессов  таковы:

Удобно также изменить единицы измерения мощности и стоимости. Пусть 10 000 часов = 1 новой единице мощности, 10 000 долл.= 1 новой единице стоимости.

Таблица 5-5-I1I

Модель о смешивании продукции (после изменения единиц)

^^^ Технологические ^^^ процессы Ингредиенты                              ^^^^	Производство столов (1=10 000 часов)	Не использовать мощность цехов столяр- отделоч­ного       ного	Экзо­генные потоки
	(1)        (2)        (3)        (4)    у1         у2           у3         у4	(5)          (6)           у5           у6
0. Общий объем работ (1=10000 часов)	1,0       1,0        1,0        1,0	1,0        1,0	1.0
1. Объем столярных работ	0,8       0,9        0,7        0,2	1,0	0,6
2. Объем отделочных работ	0,2        0,1       0,3       0,8	1,0	0,4
3. Стоимости (1=10000 долл.)	-2,4       -2,0     -1,8      -0,8		z' (min)

Тогда легко видеть (и это оставляется в качестве упражнения), что табл. 3-5-II модели смешивания продукции перейдет в табл. 3-5-III после указанных выше изменений единиц технологических процессов, замены z на 10000 z' = z в уравне­нии стоимости и сложения этих двух уравнений для того, чтобы получить уравнение общей мощности.

Теперь мы можем найти графиче­ское решение. Ввиду того что неиз­вестные y_j0 в сумме дают едини­цу, мы будем интерпретировать этот факт как приписывание неотрицатель­ных весов точкам A₁, А₂, . . . , А₆ на рис. 3-5-1. Мы будем игнорировать одно из уравнений ма­териального баланса, а именно урав­нение для ингредиента 1, мощности столярного цеха; однако мы обнаружим, что это не повлияет на минимальное решение, потому что это уравнение избыточно.

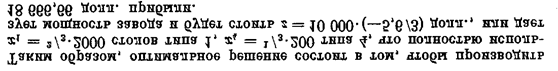
Мощность столярного цеха использована при этом решении полно­стью, несмотря на то, что соответствующее ей уравнение материального баланса в приведенных выше выкладках не фигурировало. Как уже отме­чалось ранее, это произошло потому, что добавление к системе уравнения общей мощности, дает нам возможность опустить любое из оставшихся уравнений, сохраняя при этом модель, которая учитывает все мощности;  уравнение мощности столярного цеха оказывается избыточным и может быть отброшено.