Исследование негармонических колебаний. Анализ негармонических колебаний с использованием теоремы Фурье, страница 8

Пример 1.2.Период прямоугольного сигнала Т = 200 мкс = 200 • 10^-6с, Um = 100 B. Построить и сравнить между собой спектры для длительности импульсов = 25 мкс и

= 12,5 мкс.

Решение. При Т = 200 мкс частота первой гармоники (частота повторения) составляет 1/Т = 1/200 · 10^-6 = 5000 Гц = 5 кГц. При = 25 мкс скважность                                                        

S = T/t_и = 200/25 = 8. В этом случае амплитуды составляющих спектра рассчитывают по формуле  При t_и = 12,5 мкс  Результаты расчетов сведены в таблицу 10.2 и показаны на рисунке 1.9, а, б.

Таблица 1.2 – Результаты расчетов

Продолжение таблицы 1.2

Рассмотрим теперь случай, когда t_и = const, T = var. Будем увеличивать период Т, при этом частота первой гармоники f_1, а следовательно, и расстояния между спектральными линиями - станут уменьшаться; поскольку  спектральные линии сместятся в область более низких частот и станут ближе друг к другу. Говорят, что «густота» спектра при этом  возрастает.

Пример 10.3. Сравнить спектры периодических прямоугольных сигналов, у которых

t_и = 25 мкс, Т₁ = 200 мкс, Т₂ = 400 мкс.

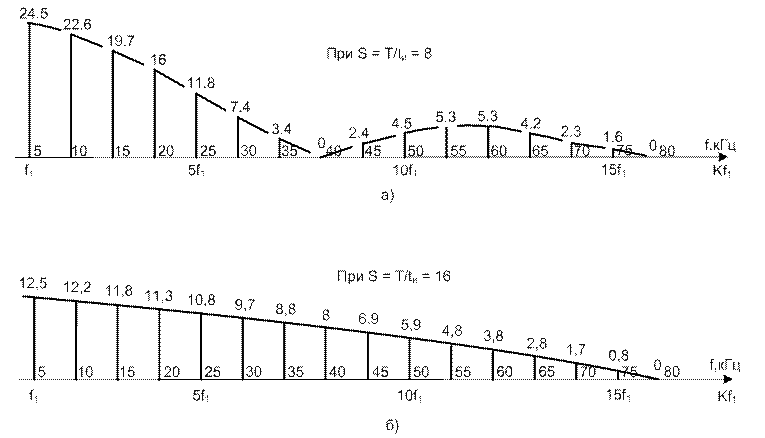
Рисунок 1.9 – Спектры сигналов со скважностями 8 и 16

Решение. В первом случае скважность S₁ = 8,  во втором S₂ = 16. Для случая S₁= 8 спектр рассмотрен в примере 1.2. Построим спектр сигнала при Т = 400 мкс., t_и = 25 мкс.

Частота первой гармоники (частота повторения) f₁ и расстояние между спектральными линиями ,  равное 1/T составляют 1/400 • 10^-6  =  2500 Гц  =  2,5 кГц (вместо 5 кГц, которые были при Т = 200 мкс).

Частота "первого нуля" останется, как и было при Т=  200 мкс., на частоте 40 кГц, но если 40 кГц  для сигнала с Т=  200 мкс. была частотой 8-й гармоники, то для Т  =  400 мкс. эти же  40 кГц становятся 16-й гармоникой, поскольку первая гармоника в этом случае оказывается на частоте 2,5 кГц и спектральные линии идут также через 2,5 кГц (рисунок 1.10). Частота 80 кГц в этом случае становится  частотой 32-й гармоники и так далее.

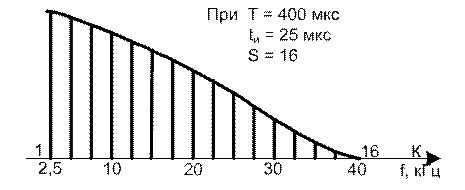
Рисунок 1.10 – Спектр сигнала при заданных параметрах

Таким образом, если, не изменяя периода Т, укорачивать длительность импульса t_и, то частота первой гармоники (частота следования) и расстояние между спектральными линиями остаются неизменными, частота «первого нуля» увеличивается, амплитуда первой гармоники уменьшается, спектр становится более равномерным. Если, не изменяя длительности импульса  t_и , увеличивать период Т, то частота первой гармоники и расстояние между спектральными линиями уменьшаются, прежние частоты становятся соответственно гармониками с большими номерами, численное значение частоты "первого нуля" остается без изменения, но эта частота является гармоникой с большим номером. По мере увеличения периода Т спектральные линии идут все чаще, густота спектра возрастает. При увеличении периода Т до бесконечности сигнал из периодического превращается в непериодический, то есть не повторяющийся во времени. В этом случае частота первой гармоники и расстояния между гармониками становятся  равными нулю, следовательно, спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга.