Дата выдачи задания 10.12.07г. _____________________
(подпись руководителя)
Задание принято к исполнению 10.12.07г. _____________________
(подпись студента)
ПРИМЕЧАНИЕ: Это задание вкладывается в законченную пояснительную записку и предоставляется в Государственную квалификационную комиссию.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ХАБАРОВСКИЙ ИНСТИТУТ ИНФОКОММУНИКАЦИЙ
ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ
ФАКУЛЬТЕТ ДНЕВНОГО ОБУЧЕНИЯ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
__________________________________________________________________________________________
руководителя на дипломный проект Валерьевича на тему:
Постановка лабораторной работы «Исследование негармонических колебаний»
Руководитель проекта: А.С.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ХАБАРОВСКИЙ ИНСТИТУТ ИНФОКОММУНИКАЦИЙ
ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ И ИНФОРМАТИКИ
ФАКУЛЬТЕТ ДНЕВНОГО ОБУЧЕНИЯ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
__________________________________________________________________________________________
руководителя на дипломный проект Валерьевича на тему:
Постановка лабораторной работы «Исследование негармонических колебаний»
Рецензент А.П.
СОДЕРЖАНИЕ
Стр.
ВВЕДЕНИЕ
1 ОБЩАЯ ЧАСТЬ
1.1 Анализ негармонических колебаний с использованием теоремы Фурье
1.1.1 Разложение периодических функций на гармонические составляющие
1.1.2 Виды симметрии периодических негармонических кривых
1.1.3 Спектральное представление сигналов
1.1.4 Спектры сигналов с прямоугольной последовательностью
1.1.5 Спектры при изменении длительности импульса и периода сигнала
1.1.6 Практическая ширина спектров сигналов
1.1.7 Иерархический ряд сигналов
2 РАСЧЕТНАЯ ЧАСТЬ
2.1 Расчет гармонических составляющих прямоугольных односторонних импульсов
2.2 Расчет колебательного контура
3 СПЕЦИАЛЬНАЯ ЧАСТЬ
3.1 Вопросы техники безопасности
3.2 Вопросы экологии
4 ЭКОНОМИЧЕСКАЯ ЧАСТЬ
4.1 Расчет стоимости методической работы «Исследование негармонических колебаний»
ПРИЛОЖЕНИЕ А
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
1 ОБЩАЯ ЧАСТЬ
1.1 Разложение периодических функций на гармонические составляющие
Все периодические сигналы (то
есть напряжения или токи), отличные от гармонических, называются
негармоническими. Каждый негармонический сигнал характеризуется периодом Т,
формой и размахом напряжения или тока (Up или Ip). Так как негармонических
сигналов существует неограниченное множество, то разработана методика, позволяющая
анализировать любые сигналы, независимо от их формы. Данная методика состоит в
том, что подбирают ряд гармонических (то есть синусоидальных или
косинусоидальных) сигналов с такими амплитудами, частотами и начальными фазами,
алгебраическая сумма ординат которых в любой момент равна ординате исходного
несинусоидального сигнала. Так, напряжение 1 на рисунке 1.1 можно заменить
напряжениями 2 и 3, поскольку мгновенные значения напряжений ![]() и
и ![]() в любой момент равны
мгновенным значениям напряжения
в любой момент равны
мгновенным значениям напряжения ![]()
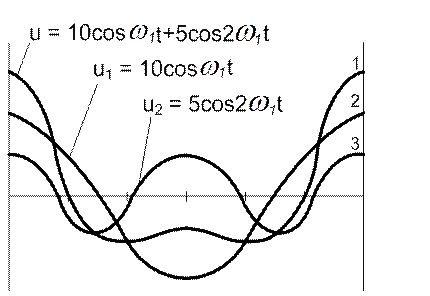
Рисунок 1.1 – Амплитудные характеристики напряжений
Рассмотрим, как можно определить амплитуды, частоты и начальные фазы гармонических составляющих, которыми заменяют заданный негармонический сигнал. Чтобы выполнить данную замену, необходимо применять несколько правил, известных из курса математики. Сущность этих правил состоит в следующем. Для воспроизведения
данной негармонической кривой можно использовать не любые синусоиды (косинусоиды), а только те, частоты которых в целое число раз отличаются от величины
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.