Систематизируем сведения о ширине спектров различных сигналов. Расположим сигналы в иерархический ряд, то есть в последовательности, соответствующей расширяющимся спектрам.
Периодический гармонический сигнал
(рисунок 1.14, а) является самым узкополосным, вся полоса состоит из одной
частоты f = 1/T. Увеличим несколько крутизну склонов,
придадим сигналу треугольную форму. В этом случае появляются высшие гармоники,
затухающие по квадратичному закону. Увеличим крутизну фронтов, превратим сигнал
в прямоугольный со скважностью 2. При этом амплитуды гармоник уменьшаются по
линейному закону и спектр соответственно расширяется. При увеличении периода Т
и неизменном tи скважность увеличивается, «первый нуль»
перемещается в область более высоких частот, спектр расширяется. Укоротим время
импульса tи, частота «первого нуля» при этом
останется прежней, но спектр расширится в области низких частот и станет более
частым. При сохранении дли![]() тельности
импульса прежним и увеличении периода до бесконечности спектр превращается
в сплошной, шириной примерно 1//и. При уменьшении длительности
импульса до бесконечно малого значения "первый нуль" перемещается в
">, спектр, следовательно, становится непрерывным, равномерным и
неограниченно широким. Импульс, бесконечно короткий, с бесконечно большой
амплитудой и площадью импульса, равной 1, называется импульсной функцией или δ-функцией (читается
"дельта-функция"). Таким образом, периодический сигнал гармонической
формы – самый узкополосный сигнал, состоящий всего из одной частоты, а
непериодический импульсный сигнал – самый широкополосный, состоящий из
бесконечно большого числа частот.
тельности
импульса прежним и увеличении периода до бесконечности спектр превращается
в сплошной, шириной примерно 1//и. При уменьшении длительности
импульса до бесконечно малого значения "первый нуль" перемещается в
">, спектр, следовательно, становится непрерывным, равномерным и
неограниченно широким. Импульс, бесконечно короткий, с бесконечно большой
амплитудой и площадью импульса, равной 1, называется импульсной функцией или δ-функцией (читается
"дельта-функция"). Таким образом, периодический сигнал гармонической
формы – самый узкополосный сигнал, состоящий всего из одной частоты, а
непериодический импульсный сигнал – самый широкополосный, состоящий из
бесконечно большого числа частот.
Четырехполюсник, не искажающий сигналы вида δ-функции, пропускает без искажения сигнал любой формы. Разумеется, δ-функция является идеализированным сигналом, на практике для получения широких спектров с амплитудами, близким к постоянным, используют короткие импульсы с большой скважностью. Как следует из вышеизложенного, испытания различных четырехполюсников (в том числе усилители и д.р.) с помощью гармонических сигналов малоэффективны. Испытания следует производить по схеме (рис. 10.15). на входж испытуемого четырехполюсника подводят сигнал, близкий к δ-функции, и по изображению напряжения на выходе четырехполюсника судят о полосе его пропускания.
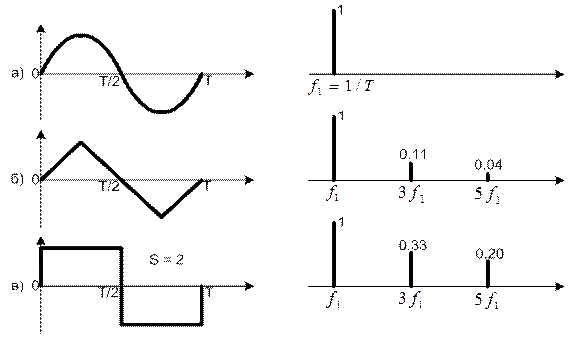
Рисунок 1.14 а-в – Иерархический ряд сигналов
![]()

Рисунок 1.14 г-ж – Иерархический ряд сигналов
2 РАСЧЕТНАЯ ЧАСТЬ
2.1 Расчет гармонических составляющих прямоугольных односторонних и двусторонних импульсов
Задача 2.1
Дано:
Um = 10 В; tи = 2 мкс; Т = 10 мкс![]()
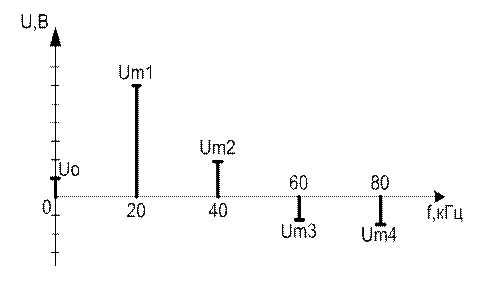
Определить: Uо; Um1; Um2; Um3; Um4
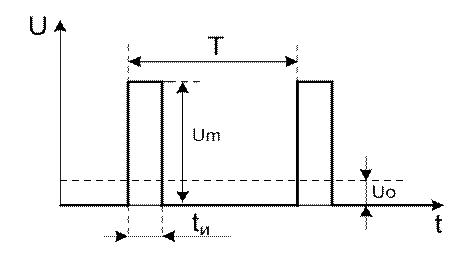
Рисунок 2.1 – Односторонние прямоугольные импульсы
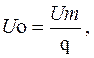 (2.1)
(2.1)
![]() где Uo – постоянная
составляющая;
где Uo – постоянная
составляющая;
Um – амплитуда прямоугольных импульсов;
q – скважность.
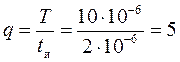 ,
(2.2)
,
(2.2)
где Т – период следования сигнала;
tи – длительность импульса.
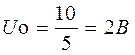
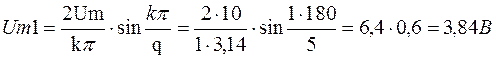 (2.3)
(2.3)
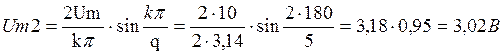
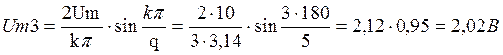
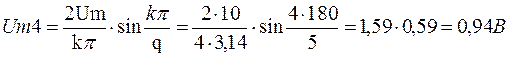
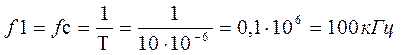
![]() (2.4)
(2.4)
![]()
![]()
![]()
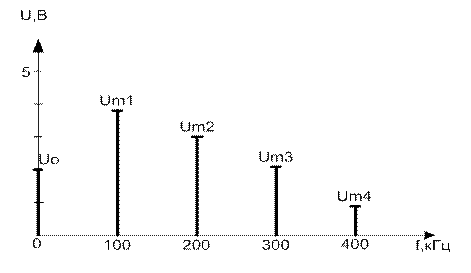
Рисунок 2.2 – Спектральная диаграмма к задаче 1
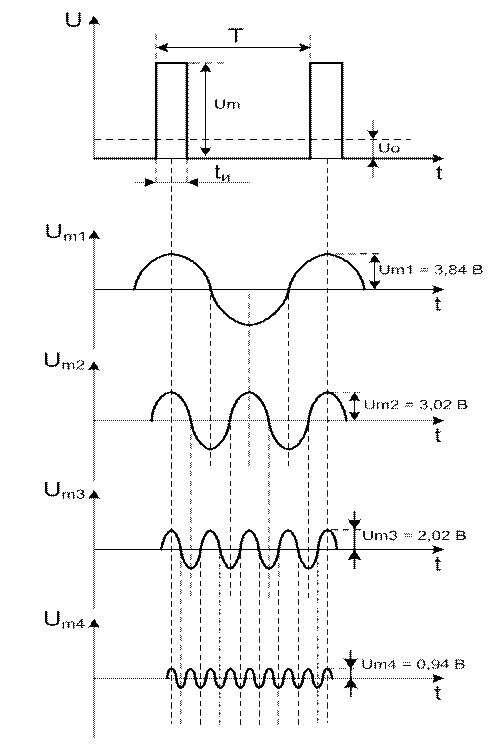
![]() Рисунок 2.3 – Гармонические
составляющие прямоугольных импульсов
Рисунок 2.3 – Гармонические
составляющие прямоугольных импульсов
Задача 2.2
Дано: Um = 10 В; tи = 10 мкс; T = 20 мкс
Определить: Uо; Um1; Um2; Um3; Um4
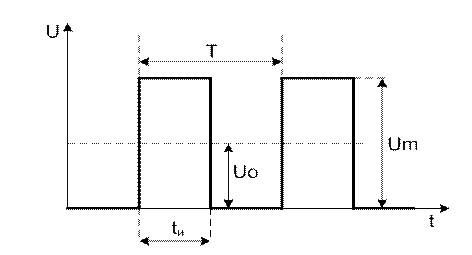
Рисунок 2.4 – Односторонний прямоугольный сигнал
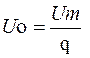
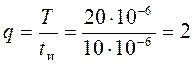
![]()
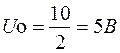
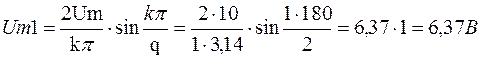
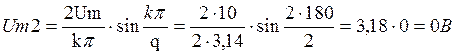
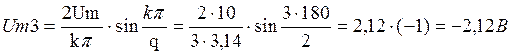
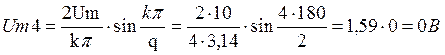
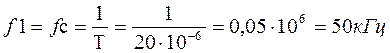
![]()
![]()
![]()
![]()
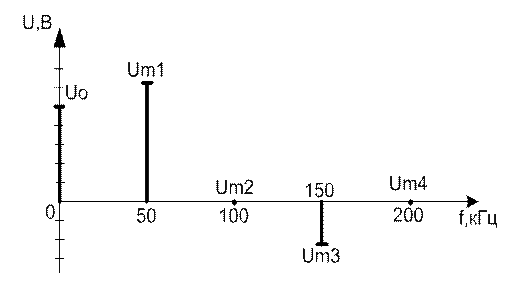
Рисунок 2.5 - Спектральная диаграмма к задаче 2
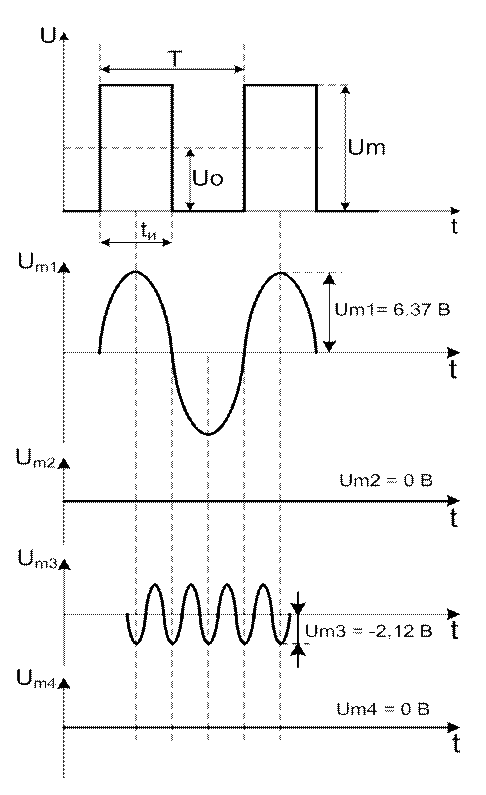
![]() Рисунок 2.6 - Гармонические
составляющие прямоугольных импульсов
Рисунок 2.6 - Гармонические
составляющие прямоугольных импульсов
Задача 2.3
Дано: tи = 20 мкс; Т = 50 мкс; Um’ = 7 В; Um’’ = 3 В
Определить: Uо; Um1; Um2; Um3; Um4
![]()
![]()
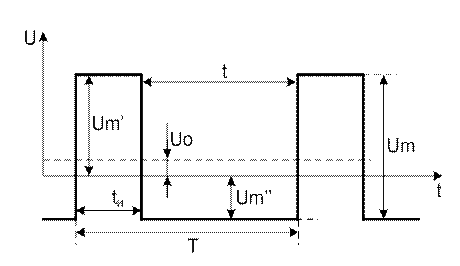
Рисунок 2.7 – Двухполярный прямоугольные импульсы
![]()
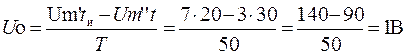 (2.5)
(2.5)
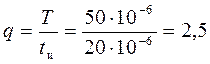
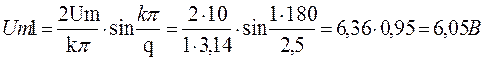
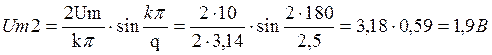
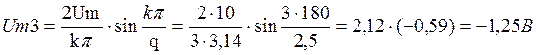
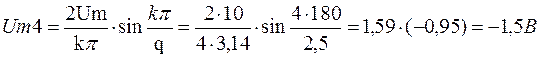
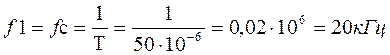
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.