Исследование негармонических колебаний. Анализ негармонических колебаний с использованием теоремы Фурье, страница 6

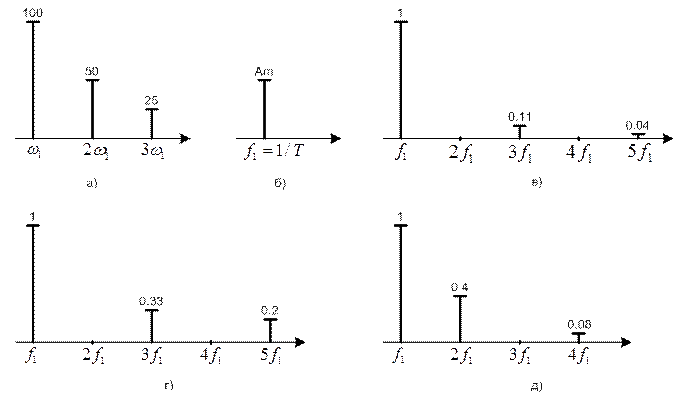
Рисунок 1.4 – Спектральное представление различных сигналов

Аналогично существуют фазные спектры, на которых по горизонтальной оси откладывают частоты, а по вертикальной - начальные фазы гармонических составляющих. Так как ряд любого периодического сигнала состоит из гармонических составляющих, отличающихся в целое число раз от частоты первой гармоники, то спектральные линии, в общем случае, находятся на расстоянии друг от друга, где - частотный интервал, равный частоте первой гармоники . Спектры, состоящие из отдельных линий, называют дискретными или линейчатыми. Таким образом, дискретные спектры периодических сигналов имеют спектральные составляющие с кратными частотами (и так далее)

Приведем примеры спектров некоторых периодических сигналов. Сигнал гармонической формы содержит только первую гармонику, поэтому спектр этого сигнала состоит из одной спектральной линии (рисунок 1.4, б). Как видно из выражения (1.9), сигналы треугольной формы состоят из гармонических составляющих с нечетными номерами, амплитуды некоторых убывают пропорционально квадрату номера гармоники. Следовательно, если амплитуду первой гармоники принять за единицу, то амплитуда второй гармоники равна нулю (Am₂ = 0), амплитуда третьей гармоники – в девять раз меньше, то есть Am₃ = 0,11, амплитуда четвертой гармоники равна нулю (Am₄ = 0), амплитуда пятой гармоники – в двадцать пять раз меньше (Am₅ = 0,04) и так далее (рисунок 1.5, в). Из выражения (1.10) следует, что у сигналов прямоугольной формы со скважностью 2 амплитуды нечетных гармонических составляющих убывают пропорционально номерам гармоник, амплитуды гармоник с четными номерами равны нулю, то есть если принять  то      где k – нечетное число (рисунок 1.5, г). Если у кривой однополупериодного вида амплитуду первой гармоники принять за единицу, то, как видно из ряда (1.11),

  . Постоянная составляющая составляет 0,637 амплитуды первой гармоники, или 0,318 амплитуды того гармонического сигнала, из которого получена данная однополупериодная кривая (рисунок 1.5, д). Таким образом, чтобы построить спектр любого периодического сигнала, необходимо знать закон мгновенных значений, то есть ряд Фурье для данного сигнала.

1.4 Спектры сигналов с прямоугольной последовательностью

Пусть имеются периодические сигналы прямоугольной формы с периодом Т, длительностями импульсов t_и и максимальным значением Um. Разложим данный сигнал в ряд. Выберем начало координат так, как показано на рисунке 1.6.

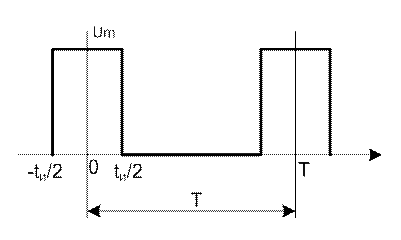
Рисунок 1.6 – Периодический сигнал прямоугольной формы

В этом случае функция оказывается симметричной относительно вертикальной оси, все коэффициенты при синусоидальных составляющих равны нулю, необходимо подсчитать только косинусоидальные коэффициенты ряда, которые являются также и общими коэффициентами членов ряда:

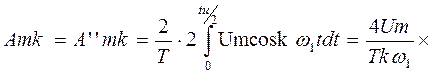
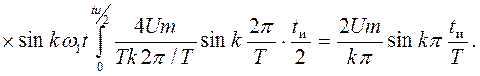                                      (1.13)

Постоянная составляющая

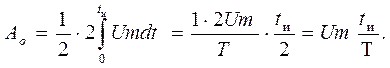                                                        (1.14)

Постоянная составляющая представляет среднее значение за период, то есть разность площадей над и под горизонтальной осью, деленную на основание, равное периоду Т. При обозначениях, показанных на рисунке 1.7,  где S₁ – площадь над горизонтальной осью, а S₂ – площадь под горизонтальной осью. В сигнале (рисунок 1.6) площадь под горизонтальной осью равна нулю, поэтому площадь , а деленная на основание ,что получилось при строгих вычислениях.

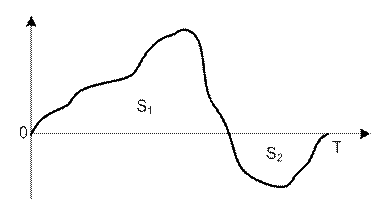
Рисунок 1.7 – Несимметричный сигнал относительно горизонтальной оси

Разберем построение спектральных характеристик. Частота первой гармоники (частота повторения) определяется из выражения , где Т – это период прямоугольного сигнала. Расстояние между гармониками  равно частоте первой гармоники, то есть . Ели номер гармоники k таков, при котором аргумент, находящийся под знаком синуса , равен 180^о, то амплитуда этой гармоники первый раз обращается в нуль. Но 180^о есть  радиан, поэтому  при  откуда . Номер гармоники, при котором амплитуда гармонической составляющей первый раз обращается в нуль, называют «первым нулем» и обозначают буквой N, чтобы подчеркнуть особые свойства гармоники с данным номером: