Исследование негармонических колебаний. Анализ негармонических колебаний с использованием теоремы Фурье, страница 5

Кривая двухполупериодной формы (рисунок 1.2, д):

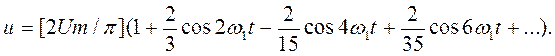                       (1.12)

1.2 Виды симметрий периодических негармонических кривых

Симметрия относительно горизонтальной оси. Кривые, удовлетворяющие условию f(t) = -f(t + T/2), являются симметричными относительно горизонтальной оси (рисунок 1.3, а). Данную симметрию можно представить следующим образом: если часть кривой, находящейся над осью времени, переместить на половину периода и при этом окажется, что перемещенная часть представляет зеркальное отображение части кривой, находящейся под осью, то такая кривая симметрична относительно горизонтальной оси. У таких кривых коэффициенты четных гармоник (в том числе и постоянной составляющей) равны нулю.

Следовательно, ряд, описывающий мгновенные значения кривых, симметричных относительно горизонтальной оси, состоит только из нечетных гармоник. Сигналы, показанные на рисунках 1.1 - 1.3, - типичные кривые, симметричные относительно горизонтальной оси, поэтому они состоят из гармоник только с нечетными номерами (1, 3, 5, 7, 9 и так далее).

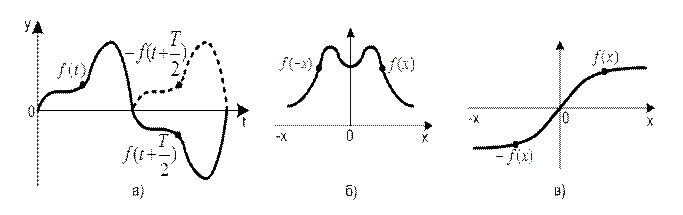
Рисунок 1.3 – Виды симметрий

Симметрия относительно вертикальной оси. Кривые,  удовлетворяющие условию       f(t) = f(-t), являются симметричными относительно вертикальной оси (рисунок 1.3, б). Симметрию относительно вертикальной оси можно представить следующим образом: если чертеж перегнуть по вертикальной оси и при этом окажется, что перегнутая часть накладывается на неперегнутую, то это означает, что данная кривая симметрична относительно вертикальной оси. У кривых, симметричных относительно вертикальной оси, коэффициенты при синусоидальных составляющих равны нулю. Следовательно,  ряд, описывающий мгновенные значения кривых, симметричных относительно вертикальной оси, состоит только из косинусоидальных составляющих с нулевыми начальными фазами каждая и постоянной составляющей. У кривых (рисунок 1.2, г и 1.2, д) начала координат выбраны так, что эти кривые симметричны относительно вертикальной оси. Именно поэтому ряды обеих кривых содержат постоянные и косинусоидальные составляющие. У однополупериодной кривой Uо = Um/π, а у двухполупериодной U_о= 2Um/π.

Симметрия относительно начала осей координат.  Кривые, удовлетворяющие условию

f (t) = -f ( -t), являются симметричными относительно начала осей координат (рисунок 1.3 в). Симметрию относительно начала осей координат можно представить следующим образом: если нарисовать кривую, представляющую зеркальное отображение верхней половины относительно вертикальной оси, и эта кривая оказывается зеркальным отображением функции относительно горизонтальной оси, то это означает, что кривая симметрична относительно начала осей координат. У кривых, симметричных относительно начала осей координат, постоянная составляющая и косинусные коэффициенты равны нулю. Следовательно, кривые, симметричные относительно начала осей координат, состоят только из синусоид с нулевыми начальными фазами каждая. Синусоидальная, треугольная  и прямоугольные кривые (рисунок 1.2, а-в) имеют по два  вида симметрии каждая: относительно горизонтальной оси (пропадают все четные гармоники) и относительно начала осей координат (пропадают все косинусные составляющие). Поэтому данные сигналы состоят только из нечетных синусоид с нулевой начальной фазой каждая, что соответствует рядам (1.8) – (1.10). Умение оценивать виды симметрии во многом облегчать разложение кривых различных сигналов и определение гармонических составляющих, из которых состоят сигналы различных форм. В некоторых случаях важно знать, каких составляющих в данном сигнале.

1.3 Спектральное представление сигналов

Совокупность гармонических составляющих, образующих сигнал несинусоидальной формы, называется спектром этого негармонического сигнала. В принципе спектры можно было бы показывать графически,  в виде временных кривых, как, например, на рисунке 1.1, однако такое изображение спектра  весьма громоздко, малонаглядно и им на практике не пользуются. Вместо каждой временной кривой рисуют вертикальную линию, длина которой пропорциональна амплитудному значению данной составляющей, а место на горизонтальной оси определяется частотой данной составляющей. Например, если мгновенные значения некоторого периодического несинусоидального сигнала описываются рядом , то спектр данного сигнала имеет вид, показанный на рисунке 1.4, а. На данном спектре показана амплитуда каждой спектральной составляющей, поэтому такой спектр называют амплитудным спектром.