Исследование негармонических колебаний. Анализ негармонических колебаний с использованием теоремы Фурье, страница 4

1/Т, где Т – период негармонического сигнала. Например, если имеется несколько периодических негармонических сигналов с различными формами, но одинаковым периодом Т, допустим по 1 мс, то для формирования таких негармонических сигналов пригодны только синусоидальные сигналы с частотами, кратными значению 1/Т = 1/10³ = 10³ Гц = 1 кГц, т.е. 2, 3, 4 кГц и т.д., но совершенно непригодны любые синусоиды с частотами, отличными от k (1/Т), где k – целое положительное число. Гармоническая составляющая, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой данного негармонического сигнала, в некоторых случаях – частотой повторения, а иногда – частотой следования. Все остальные составляющие называются высшими гармониками или высшими гармоническими составляющими, причем гармоника, частота которой в два раза больше частоты основной гармоники, называется «второй гармоникой», гармоника, частота которой в три раза больше  - «третьей гармоникой» и так далее. Каждая гармоника может состоять либо только из синусоиды с соответствующей частотой, но с ненулевой начальной фазой, либо из синусоиды и косинусоиды, но с нулевыми начальными фазами каждая. В последнем случае называют: «синусоидальная составляющая k – й гармоники» и «косинусоидальная составляющая k – й гармоники». Это обстоятельство вытекает из известного тригонометрического соотношения:

    (1.1)

где

На практике сначала находят амплитуды синусоидальной  и косинусоидальной  составляющих каждой гармоники, а затем определяют амплитуду  и начальную фазу общей синусоидальной кривой данной гармоники: 

                                                                                 (1.2)

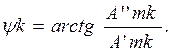                                                                                                      (1.3)

Амплитуды синусоидальной и косинусоидальной  составляющих находят по формулам, известным из математики как формулы для определения коэффициентов ряда Фурье [Жан Фурье (1772 - 1837) французский математик и физик, в 1829 г. избран почетным членом Петербургской академии наук], то есть:

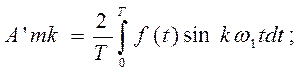                                                                            (1.4)

                                                                               (1.5)

где k – номер гармоники; - математическое выражение, описывающее закон, по которому изменяются мгновенные значения той негармонической кривой, для которой определяются гармоники; Т – период негармонической кривой;  - угловая частота первой гармоники негармонической кривой .

Кроме гармонических составляющих может быть постоянная составляющая данного негармонического сигнала:

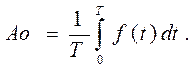                                                                                                 (1.6)

Таким образом, мгновенные значения любого периодического негармонического сигнала записывают в виде математического выражения, представляющего сумму гармонических составляющих и постоянной составляющей, известного под названием ряда Фурье. Заметим, что постоянную составляющую часто рассматривают как гармонику с нулевым номером и поэтому говорят только о гармонических составляющих, не упоминая отдельно о постоянной составляющей сигнала. Если мгновенные напряжения некоторого негармонического сигнала имеют значения , то такое негармоническое напряжение можно представить рядами Фурье.

                                        (1.7)

Покажем ряды, получившиеся при разложении некоторых типовых сигналов. Синусоидальная кривая (рисунок 1.2,а) представляет частный случай негармонического сигнала, у которого при разложении в ряд амплитуды всех высших гармоник равны нулю:

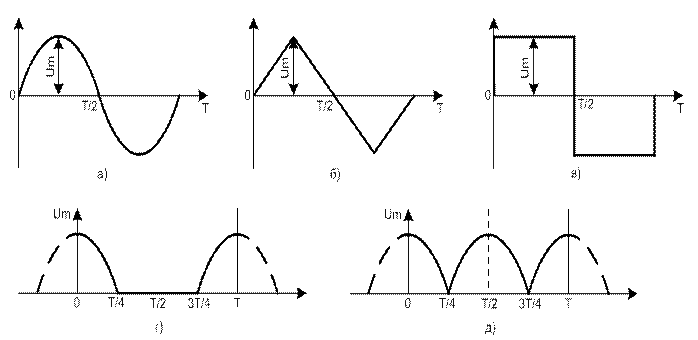
Рисунок 1.2 – Частные случаи периодических сигналов различных форм

.                                                                                                            (1.8)

Кривая треугольной формы (рисунок 1.2, б):

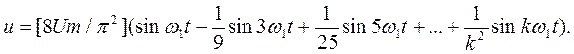                     (1.9)

Кривая прямоугольной формы (рисунок 1.2, в):

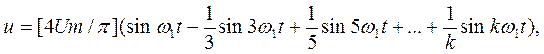                         (1.10) где k – целое нечетное число.

Кривая однополупериодной формы (рисунок 1.2, г):

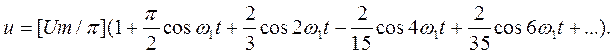
        (1.11)