Исследование негармонических колебаний. Анализ негармонических колебаний с использованием теоремы Фурье, страница 7

                                                                                                                   (1.15)

Но отношение периода Т к длительности импульса t_и есть скважность S. Таким образом, «первый нуль» численно равен скважности импульса, так как синус выражения (1.13) становится равным нулю при всех значениях, кратных 180^о, то амплитуды всех гармоник, номера которых кратны номеру «первого нуля», также имеют нулевые значения. Следовательно,  при , где n – любое целое число. Из выражения (1.10) видно, что ряд сигналов прямоугольной формы со скважностью S = 2 состоит только из нечетных гармоник. Разберем, почему так получается.

Если скважность сигнала S = 2, то, следовательно, «первый нуль» приходится на вторую гармонику. Но нулевыми будут также коэффициенты всех гармоник, номера которых кратны двум. Аналогично, при скважности S = 3 нулевые амплитуды будут у 3, 6, 9, 12,…гармоник, при S = 4 не будет 4, 8, 12, 16,…гармоник и так далее. По мере увеличения скважности «первый нуль» перемещается в область гармоник с большими номерами и, следовательно, скорость убывания амплитуд гармоник уменьшается.

Пример 1.1 Рассчитать спектры сигналов прямоугольной формы со скважностями S = 2, 3, 4, 5, 10 для первых десяти гармоник, если амплитуда сигнала Um = 100 B.

Решение. Амплитуды составляющих для сигналов прямоугольной формы определяются из выражения  где k – номер гармоники.

Результаты занесем в таблицу 1.1:

Таблица 1.1 – Расчет гармонических составляющих, при изменяющейся скважности

Для S = 2 .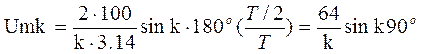

При k = 1 .

При k = 2 .

При k=3 и так далее.

Для S = 3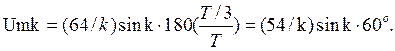

Для S = 4

Для S = 5

Для S = 10

Построим спектры для S =2, S =5, S =10 (рисунок 1.8).

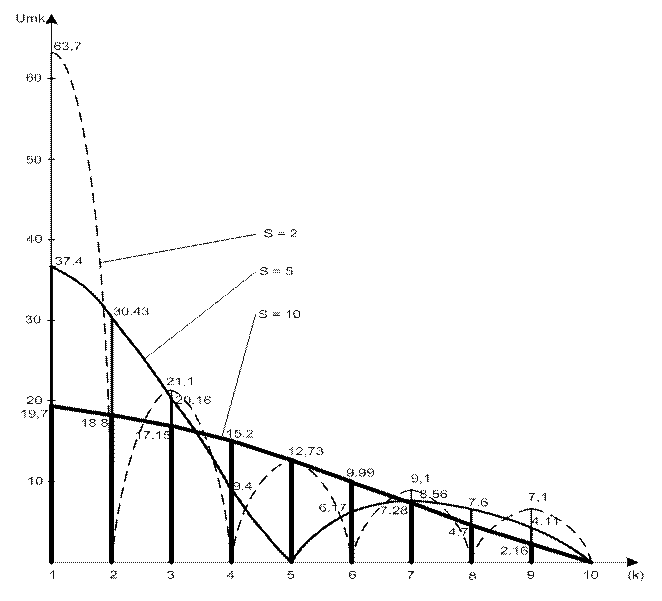
Рисунок 1.8 – Спектры сигналов со скважностями 2, 5 и 10

Из данного расчета видно, что чем больше скважность прямоугольного сигнала, тем меньше абсолютное значение имеет амплитуда напряжения первой гармоники, но тем медленнее уменьшаются амплитуды гармонических составляющих, то есть тем равномернее становится спектр. Например, при скважности S = 2 ряд имеет вид:

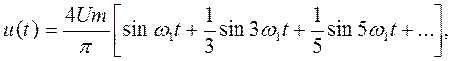
из которого видно, что отношение амплитуды пятой гармоники Um₅ к амплитуде первой гармоники Um₁ равно 0,2. При скважности S = 10 ряд описывается выражением:

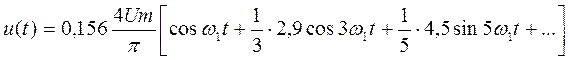
и отношение Um₅/Um₁ в этом случае становится 0,9, то есть скорость затухания для пятой гармоники уменьшается в 4,5 раза и так далее.  

1.5 Спектры при изменении длительности импульса сигнала

Скважность 5 = T/t_иможно регулировать двумя способами: либо изменением длительности импульса t_и при постоянном периоде Т, либо изменением периода Т при постоянной длительности импульса t_и. В обоих случаях спектры получаются различными. Рассмотрим сначала вариант Т = const, t_и = var. Здесь частота первой гармоники f_tи расстояния между гармониками  остаются неизменными, равными 1/Т. «Первый нуль» равен Т/t_и и по мере укорочения импульса t_и передвигается в сторону гармоник с большими номерами. При "первый нуль" стремится  в бесконечность, спектр получается дискретным с частотой дискретизации f₁ = 1/Т, бесконечно широкий с бесконечно малыми амплитудами.