






























1 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
1.1.1 Обыкновенным дифференциальным уравнением называется равенство, в которое входят независимая переменная, неизвестная функция этой переменной и её производные ( или дифференциалы). Общий вид:
![]()
или:
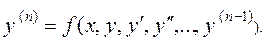
В дальнейшем слово «обыкновенные» будем опускать, слово «дифференциальные» будем писать как «диф.».
1.1.2 Порядком диф. уравнения называется порядок старшей производной, входящей в него. Например, уравнение:
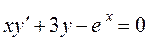 - уравнение 1-го порядка;
- уравнение 1-го порядка;
![]() -
уравнение 2-го порядка.
-
уравнение 2-го порядка.
1.1.3 Степенью
диф. уравнения называется показатель степени старшей производной, входящей в
уравнение. Например, уравнение: 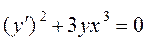 -
уравнение 1-го порядка, 2-ой степени.
-
уравнение 1-го порядка, 2-ой степени.
Диф. уравнения степенью выше единицы вначале решают алгебраически относительно старшей производной, а затем рассматривают диф. уравнения 1-ой степени относительно старшей производной. В дальнейшем будем рассматривать диф. уравнения только 1-ой степени.
1.1.4 Решением диф. уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
1.1.5 решение диф. уравнения, записанное в неявной форме называется интегралом диф. уравнения. Решения (интегралы) диф. уравнений разделяют на общие, частные и особые.
1.1.6 Общее решение содержит чаще всего всё многообразие решений и помимо независимой переменной всегда содержит столько произвольных постоянных, каков порядок диф. уравнения.
1.1.7 Частные решения находят из общего решения при конкретных численных значениях произвольных постоянных, входящих в него. Для выделения частного решения из общего диф. уравнению задают дополнительные условия в количестве равном порядку уравнения.
1.1.8 Дополнительные условия к диф. уравнению «n» порядка, заданные в виде значений функции и её производных до «n-1» порядка включительно при одном и том же значении аргумента называются начальными условиями или условиями Коши.
1.1.9 Задача нахождения частного решения диф. уравнения удовлетворяющего начальным условиям, называется задачей Коши.
1.1.10 Решения диф. уравнения, которые не содержатся в общем решении, называются особыми решениями.
1.1.11 Вместо термина «решить диф. уравнение» часто употребляется термин «проинтегрировать диф. уравнение».
1.1.12 Если решение диф. уравнения можно записать через неопределённые (или определённые) интегралы, то употребляется термин «диф. уравнение интегрируемо в квадратурах».
1.2 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Рассмотрим диф.
уравнение: ![]() .
Начальное условие Коши к нему имеет вид: y(x0) = y0 (т.е. y = y0 при x = x0) (рисунок 1.1).
.
Начальное условие Коши к нему имеет вид: y(x0) = y0 (т.е. y = y0 при x = x0) (рисунок 1.1).
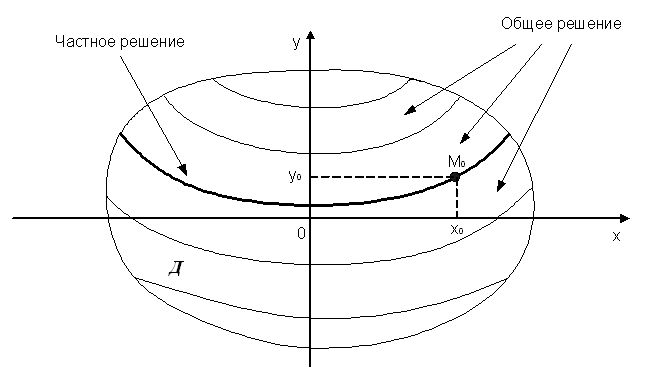
Рисунок 1.1
Обозначим область определения функции f(x,y) на плоскости Оху как область Д. С геометрической точки зрения диф. уравнение в области Д определяет «поле направлений»: в каждой точке этой области можно построить элемент касательной к неизвестной кривой, решению диф. уравнения, проходящей через эту точку. Начальное условие задаёт в этой области одну конкретную точку (М0). Графически решения диф. уравнения изображаются линиями, которые называются интегральными кривыми.
Общее решение
диф. уравнения ![]() имеет
вид y=φ (x,c), где с – произвольная
постоянная. Оно определяет семейство интегральных кривых, проходя через точки
поля, имеют элементы касательных своими касательными. Частное решение – это
одна интегральная кривая, проходящая через точку, заданную начальным условием.
В некоторых случаях общее решение диф. уравнения определяет такое семейство
интегральных кривых, которые имеют огибающую, т.е. линию, которая касается всех
линий семейства, огибающая и будет особым решением уравнения. Особые решения
могут быть только у некоторых типов уравнений, мы им отдельного внимания
уделять не будем. Если поставлена задача Коши для диф. уравнения 1-го порядка:
найти решение уравнения
имеет
вид y=φ (x,c), где с – произвольная
постоянная. Оно определяет семейство интегральных кривых, проходя через точки
поля, имеют элементы касательных своими касательными. Частное решение – это
одна интегральная кривая, проходящая через точку, заданную начальным условием.
В некоторых случаях общее решение диф. уравнения определяет такое семейство
интегральных кривых, которые имеют огибающую, т.е. линию, которая касается всех
линий семейства, огибающая и будет особым решением уравнения. Особые решения
могут быть только у некоторых типов уравнений, мы им отдельного внимания
уделять не будем. Если поставлена задача Коши для диф. уравнения 1-го порядка:
найти решение уравнения ![]() при
условии y(x0) = y0 , то важно знать, имеется ли такое
решение, если да, то как его найти. Ответ на первую часть этого вопроса
содержится в теореме.
при
условии y(x0) = y0 , то важно знать, имеется ли такое
решение, если да, то как его найти. Ответ на первую часть этого вопроса
содержится в теореме.
Теорема (существования и единственности решения).
Если поставлена
задача Коши: ![]() ;
y(x0) = y0, и функция f(x,y) - непрерывна в области, содержащей
точку (х0;у0) , то уравнение имеет решение. Если
при этом в той же области непрерывна и
;
y(x0) = y0, и функция f(x,y) - непрерывна в области, содержащей
точку (х0;у0) , то уравнение имеет решение. Если
при этом в той же области непрерывна и ![]() ,
то это решение единственное.
,
то это решение единственное.
Ответ на вторую часть вопроса дан в п.п.3, 4, 5.
1.3 ДИФ. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ.
Если в диф.
уравнении ![]() функция
функция
![]() может
быть представлена в виде:
может
быть представлена в виде: ![]() ,
то уравнение называется уравнением с разделяющимися переменными. Его решение
(интегрирование) проводится по следующему алгоритму:
,
то уравнение называется уравнением с разделяющимися переменными. Его решение
(интегрирование) проводится по следующему алгоритму:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.