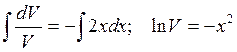 ,
здесь С = 0, т.е. рассматривается
частное решение. Откуда:
,
здесь С = 0, т.е. рассматривается
частное решение. Откуда: ![]()
Подставим в уравнение (2) и найдём его общее решение:
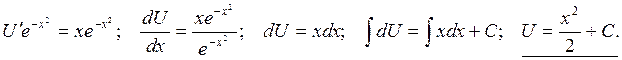
Общее решение
линейного уравнения: 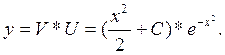
Примеры для самостоятельного решения
I. Решить уравнения с разделяющимися переменными
1. ![]()
2. 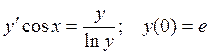
3. ![]()
4. ![]()
5. ![]()
Ответы:
1. ![]()
2. 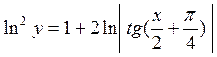
3. 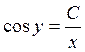
4. ![]()
5. 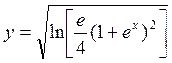
II. Решить однородные уравнения
6. ![]() 9.
9.
![]()
7. 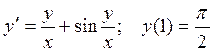 10.
10.
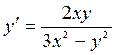
8. 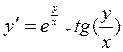
Ответы:
6. 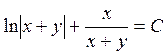 9.
9.
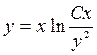
7. ![]() 10.
10.
![]()
8. ![]()
III. Решить линейные уравнения
11. 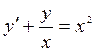 14.
14.
![]()
12. ![]() 15.
15.
![]()
13. ![]()
Ответы:
11. 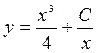 14.
14.
![]()
12. ![]() 15.
15.
![]()
13. 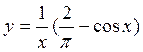
IV. Решить диф. уравнения 1-го порядка
16. 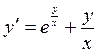 19.
19.
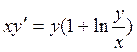
17. ![]() 20.
20.
![]()
18. ![]() 21.
21.
![]()
22. ![]()
Ответы:
16. ![]() 20.
20.
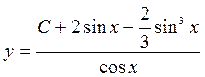
17. 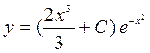 21.
21.
![]()
18. ![]() 22.
22.
![]()
19. ![]()
1.6 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Общий вид записи
диф. уравнения 2-го порядка: ![]() или
или
![]() .
Общее решение (общий интеграл) будет содержать две произвольные постоянные:
.
Общее решение (общий интеграл) будет содержать две произвольные постоянные: ![]() .
Начальные условия Коши для выделения частного решения из общего запишутся в
виде:
.
Начальные условия Коши для выделения частного решения из общего запишутся в
виде:
![]()
где α и β – действительные числа. Если в уравнении 2-го порядка не содержатся явно х или у, то уравнение называется неполным. Неполные уравнения решаются методом понижения порядка уравнения. Рассмотрим 2 случая:
I.В диф. уравнении нет явно у.
Уравнение имеет
вид: ![]() .
Вводим новую функцию:
.
Вводим новую функцию: ![]() тогда
тогда
![]() .
.
Подставляя в
уравнение, получим ![]() -
диф. уравнение 1-го порядка относительно функции z. Решив уравнение, получим
-
диф. уравнение 1-го порядка относительно функции z. Решив уравнение, получим ![]() -
первый интеграл уравнения. Интегрируя
-
первый интеграл уравнения. Интегрируя ![]() -
получим общее решение диф. уравнения 2-го порядка.
-
получим общее решение диф. уравнения 2-го порядка.
Пример 5. Проинтегрировать уравнение 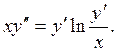
Решение: Это –
диф. уравнение 2-го порядка, неполное, т.к. в уравнении нет у. Положим: ![]()
![]() ,
подставляем в уравнение:
,
подставляем в уравнение: 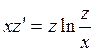 или
или
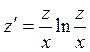 .
Это – однородное уравнение 1-го порядка, решаем его:
.
Это – однородное уравнение 1-го порядка, решаем его: 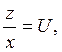 где
где
![]() .
.
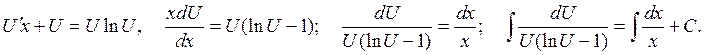
Интегрируем: ![]() .
Принимаем
.
Принимаем ![]() для
дальнейших преобразований.
для
дальнейших преобразований. 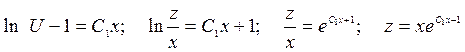 .
.
![]() -
первый интеграл уравнения.
-
первый интеграл уравнения.
Откуда 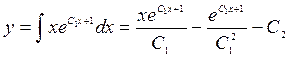 -
это общее решение уравнения, интегрирование проводилось методом «по частям».
-
это общее решение уравнения, интегрирование проводилось методом «по частям».
II. В диф. уравнении 2-го порядка нет
явно х. Уравнение имеет вид: ![]() .
Вводим новую функцию
.
Вводим новую функцию ![]() тогда
тогда
![]() Подставляем
в уравнение:
Подставляем
в уравнение: ![]() -
уравнение 1-го порядка. Решив его, найдём
-
уравнение 1-го порядка. Решив его, найдём ![]() -
первый интеграл уравнения, это уравнение с разделяющимися переменными. Так как
-
первый интеграл уравнения, это уравнение с разделяющимися переменными. Так как  то
то
 .
.
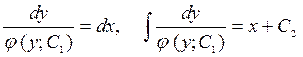 -
общий интеграл уравнения.
-
общий интеграл уравнения.
Пример 6. Проинтегрировать уравнение
![]()
Решение: Найдём
общее решение уравнения. Так как в уравнении нет х, то положим ![]() тогда
тогда
![]() Подставляем
в уравнение:
Подставляем
в уравнение: ![]() так
как
так
как 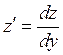 ,
получаем:
,
получаем: 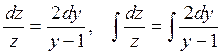 или
или
![]()
![]() т.е.
т.е.
![]() -
первый интеграл уравнения.
-
первый интеграл уравнения.
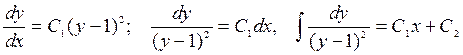 ,
т.е.
,
т.е. 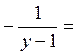
![]() .
.
После
преобразований: 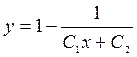 -
общее решение уравнения. Так как к уравнению заданы начальные условия, то
выделим из общего решения частное, для этого используем общее решение уравнения
и первый интеграл. Подставляя в них начальные условия:
-
общее решение уравнения. Так как к уравнению заданы начальные условия, то
выделим из общего решения частное, для этого используем общее решение уравнения
и первый интеграл. Подставляя в них начальные условия: ![]() получим:
получим:
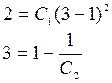 ,
откуда
,
откуда 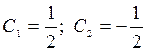 .
.
Частное решение
уравнения: 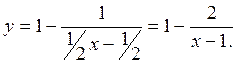 .
.
Примеры для самостоятельного решения
Найти общее решение уравнений 2-го порядка.
1. ![]() 5.
5.
![]()
2. ![]() 6.
6.
![]()
3. ![]() 7.
7.![]()
4. ![]()
Ответы:
1. ![]() 5.
5.
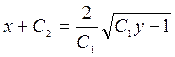
2. 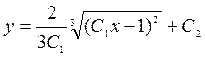 6.
6.
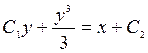
3. ![]() 7.
7.
![]()
4. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.