Характеристическое
уравнение ![]() корни
корни
![]()
Находим частное
решение неоднородного уравнения: ![]() при
этом
при
этом ![]()
![]()
Дальнейшее решение ведём по той же схеме:
![]()
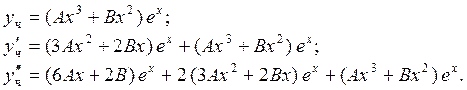
![]()
![]() т.е.
т.е.
![]() ,
откуда
,
откуда ![]() ;
;
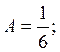
![]()
![]()
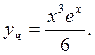
Общее решение
линейного неоднородного уравнения 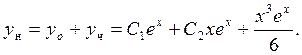
III. ![]() где
где ![]() -
действительные числа.
-
действительные числа.
Обозначим корни
характеристического уравнения через ![]() .
При записи вида частного решения линейного неоднородного уравнения проводится
сравнение с корнями характеристического уравнения комплексного числа
.
При записи вида частного решения линейного неоднородного уравнения проводится
сравнение с корнями характеристического уравнения комплексного числа ![]() где
где
![]()
![]() не корень характеристического уравнения, корень характеристического уравнения.
не корень характеристического уравнения, корень характеристического уравнения.
Коэффициенты ![]() находятся
из системы, получаемой после подстановки частного решения в уравнение
приравниванием коэффициентов при
находятся
из системы, получаемой после подстановки частного решения в уравнение
приравниванием коэффициентов при ![]() слева
и справа.
слева
и справа.
Заметим, что вид частного решения
сохранится и в том случае, если одно из чисел ![]() будет
равно нулю.
будет
равно нулю.
Пример 13. Найти общее решение
уравнения ![]()
Решение: Решим соответствующее однородное уравнение:
![]()
![]()
Найдём частное решение неоднородного уравнения:
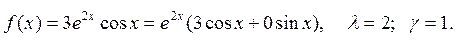
Так как число ![]() =
=
![]() не
корень характеристического уравнения, то запишем частное решение в виде:
не
корень характеристического уравнения, то запишем частное решение в виде: ![]()
Дальнейшее решение проведём по схеме:
![]()
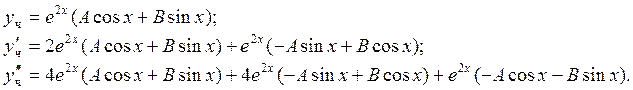
![]()
![]()
![]()
Коэффициенты при ![]() :
:
![]() =3
=3
Коэффициенты при ![]() :
:
![]() =0
=0
Откуда: 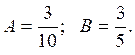
Частное решение
уравнения: 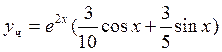 .
.
IV. Общий случай: ![]() - действительные числа,
- действительные числа, ![]() -
многочлены степеней
-
многочлены степеней ![]() .
.
Обозначим
наибольшее из чисел ![]() через
через
![]() .
.
Частное решение однородного уравнения определяется так:
1) ![]() если число
если число ![]() не
является корнем характеристического уравнения.
не
является корнем характеристического уравнения.
2) ![]() если число
если число ![]() является
корнем характеристического уравнения.
является
корнем характеристического уравнения.
Здесь ![]() -
многочлены степени
-
многочлены степени ![]() с
неопределёнными коэффициентами, которые определяются теми же приёмами, что
изложено ранее.
с
неопределёнными коэффициентами, которые определяются теми же приёмами, что
изложено ранее.
V. ![]() , где функции
, где функции ![]() соответствуют выше
разобранным случаям. Частное решение уравнения следует находить с учётом
теоремы 5.
соответствуют выше
разобранным случаям. Частное решение уравнения следует находить с учётом
теоремы 5.
Пример 14. Решить уравнение 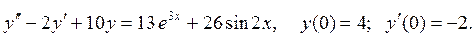
Решение:
1) Находим общее
решение соответствующего однородного уравнения: ![]() ,
,
Характеристическое
уравнение: ![]()
Корни уравнения ![]()
2) Находим
частное решение неоднородного уравнения. Так как ![]() т.е.
сумма двух функций
т.е.
сумма двух функций ![]() то
то
![]()
где ![]() -
частное решение уравнения
-
частное решение уравнения ![]()
![]() -
частное решение уравнения
-
частное решение уравнения ![]()
а) Рассмотрим
уравнение ![]()
![]() корни
характеристического уравнения найдены ранее:
корни
характеристического уравнения найдены ранее: ![]() т.к.
λ не является корнем характеристического уравнения, тогда
т.к.
λ не является корнем характеристического уравнения, тогда
![]()
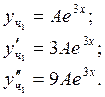
![]()
б) Рассмотрим
уравнение ![]()
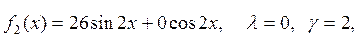
![]() -
не является корнем характеристического уравнения.
-
не является корнем характеристического уравнения.
![]()
![]()
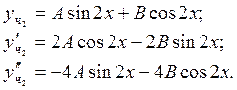
![]()
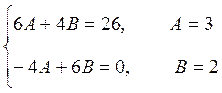
![]()
Следовательно, ![]()
3) Находим общее решение неоднородного уравнения:
![]()
4) Находим
частное решение неоднородного уравнения в соответствии с начальными условиями.
Запишем общее решение: ![]()
Найдём ![]()
Подставим в ![]() начальные
условия:
начальные
условия: ![]() получим
систему:
получим
систему:
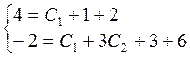
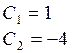
Частное решение: ![]()
Задачи для самостоятельного решения
Решить уравнения:
1.
![]() Ответ:
Ответ:
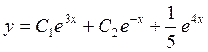
2.
![]() Ответ:
Ответ:
![]()
3.
![]() Ответ:
Ответ:
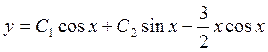
4.
![]() Ответ:
Ответ:
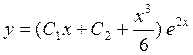
5.
![]() Ответ:
Ответ:
![]()
6.
![]() Ответ:
Ответ:
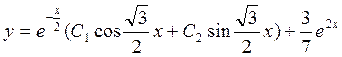
7.
![]() Ответ:
Ответ:
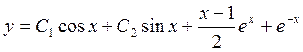
8.
![]() Ответ:
Ответ:
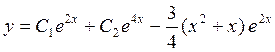
Найти частное решение, удовлетворяющее данным условиям:
1.
![]() Ответ:
Ответ:

2.
![]() Ответ:
Ответ:
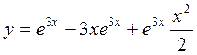
3.
![]() Ответ:
Ответ:
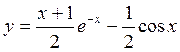
4.
![]() Ответ:
Ответ:
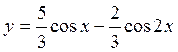
5.
![]() Ответ:
Ответ:
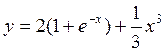
6.
![]() Ответ:
Ответ:
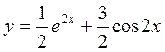
7.
![]() Ответ:
Ответ:
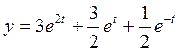
8.
![]() Ответ:
Ответ:
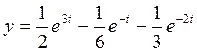
9.
![]() Ответ:
Ответ:
![]()
10. ![]()
Ответ: ![]()
11. ![]()
Ответ: ![]()
12. ![]() Ответ:
Ответ:
![]()
13. ![]() Ответ:
Ответ:
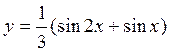
14. ![]()
Ответ: ![]()
15. ![]() Ответ:
Ответ:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.