2 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА
2.1 ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФ. УРАВНЕНИЯ 2-ГО ПОРЯДКА
Диф. уравнение
вида: ![]() называется
линейным однородным диф. уравнением 2-го порядка. Здесь
называется
линейным однородным диф. уравнением 2-го порядка. Здесь ![]() -
коэффициенты уравнения, непрерывные функции.
-
коэффициенты уравнения, непрерывные функции.
Заметим,
однородное линейное уравнение всегда имеет решение ![]() ,
это решение называется тривиальным, в дальнейшем оно рассматриваться не будет.
,
это решение называется тривиальным, в дальнейшем оно рассматриваться не будет.
Определение: Два решения уравнения ![]() называются
линейно-независимыми, если
называются
линейно-независимыми, если 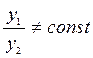 .
Если
.
Если 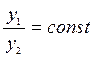 ,
то они называются линейно-зависимыми (в этом случае одно решение получается из
другого умножением на постоянную величину).
,
то они называются линейно-зависимыми (в этом случае одно решение получается из
другого умножением на постоянную величину).
Теорема 1: (Структура общего решения линейного однородного диф. уравнения 2-го порядка).
Если известны два
линейно-независимых решения уравнения ![]() ,
,
![]() ,
то общее решение уравнения определяется по формуле:
,
то общее решение уравнения определяется по формуле: ![]() где
где
![]() -
произвольные постоянные.
-
произвольные постоянные.
Определение: Два линейно-независимых решения линейного однородного диф. уравнения 2-го порядка составляют фундаментальную систему решений.
Таким образом, если каким-либо методом найти фундаментальную систему решений линейного однородного диф. уравнения, то по теореме 1 можно найти общее решение этого уравнения.
Теорема 2. Если ![]() есть
решение линейного однородного уравнения, то второе линейно-независимое решение
можно найти по формуле:
есть
решение линейного однородного уравнения, то второе линейно-независимое решение
можно найти по формуле: 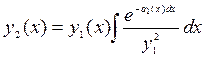 .
.
Пример 7. Рассмотрим уравнение ![]()
Решение: Можно
убедиться подстановкой в уравнение, что ![]() есть
решение уравнения. Тогда:
есть
решение уравнения. Тогда: 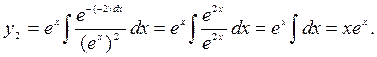
По теореме 1
общее решение уравнения: ![]()
2.2 ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим
уравнение ![]() ,
где
,
где ![]() -
числа. Согласно теореме о структуре решения необходимо найти фундаментальную
систему решений. Будем искать решение уравнения в виде
-
числа. Согласно теореме о структуре решения необходимо найти фундаментальную
систему решений. Будем искать решение уравнения в виде ![]() -
неизвестное число,
-
неизвестное число, ![]() подставляя
в уравнение
подставляя
в уравнение ![]() .
.
Так как ![]() ,
то для нахождения k получаем уравнение:
,
то для нахождения k получаем уравнение: ![]() Это
уравнение называется характеристическим. Корни этого квадратного уравнения:
Это
уравнение называется характеристическим. Корни этого квадратного уравнения: ![]()
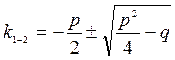 .
.
В зависимости от величины
дискриминанта 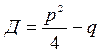 возможны
3 случая:
возможны
3 случая:
1. Д >0, тогда ![]()
В этом случае
можно сразу записать фундаментальную систему решений линейного однородного диф.
уравнения: ![]() .
И по теореме 1 найти общее решение уравнения:
.
И по теореме 1 найти общее решение уравнения: ![]() .
.
2. Д = 0, тогда 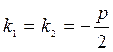 .
.
В этом случае
можно найти одно решение диф. уравнения: ![]() .
Второе решение можно найти по теореме 2:
.
Второе решение можно найти по теореме 2: 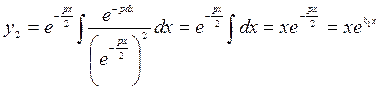 .
Общее решение линейного однородного диф. уравнения запишется в виде:
.
Общее решение линейного однородного диф. уравнения запишется в виде: ![]() .
.
3. Д < 0, корни характеристического уравнения комплексно-сопряжённые:
![]() ,
где
,
где 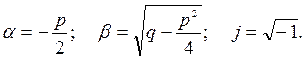
Фундаментальная
система решений линейного однородного диф. уравнения в этом случае имеет вид: ![]() а
общее решение уравнения:
а
общее решение уравнения: ![]()
Пример 8. Решить уравнение ![]()
Решение: Запишем
характеристическое уравнение ![]() .
Его корни
.
Его корни 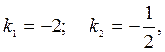 т.е.
т.е.
![]() .
Общее решение уравнения:
.
Общее решение уравнения: ![]()
Пример 9. Решить уравнение ![]()
Решение: Характеристическое уравнение
![]() его
корни
его
корни ![]() Общее
решение уравнения:
Общее
решение уравнения: ![]()
![]()
Пример 10. Решить уравнение ![]()
Решение:
Характеристическое уравнение ![]() его
корни
его
корни ![]()
Общее решение
уравнения ![]()
2.3 ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА
Рассмотрим уравнение:
![]()
где ![]() -
правая часть уравнения,
-
правая часть уравнения,
![]() -
непрерывные функции.
-
непрерывные функции.
Уравнение
![]()
называется соответствующим однородным уравнением.
Теорема 3. (Структура общего решения линейного неоднородного диф. уравнения).
Общее решение линейного
неоднородного диф. уравнения состоит из суммы двух решений: общего решения
соответствующего однородного линейного диф. уравнения и любого частного решения
неоднородного уравнения: ![]() ,
где
,
где ![]() -
общее решение соответствующего однородного диф. уравнения,
-
общее решение соответствующего однородного диф. уравнения, ![]() -
частное решение неоднородного уравнения.
-
частное решение неоднородного уравнения.
Так как вопрос нахождения ![]() рассмотрен
ранее, то необходимо выяснить, как находить частное решение неоднородного
линейного диф. уравнения.
рассмотрен
ранее, то необходимо выяснить, как находить частное решение неоднородного
линейного диф. уравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.