Теорема 4. (Нахождение частного решения линейного неоднородного диф. уравнения методом вариации произвольных постоянных).
Если дано уравнение
![]()
и известно общее решение соответствующего однородного уравнения
![]()
то частное решение неоднородного уравнения можно искать в виде:
![]()
где функции ![]() находятся
интегрированием решений системы:
находятся
интегрированием решений системы: 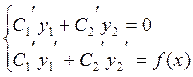 .
.
Пример 11. Найти общее решение
уравнения ![]()
Решение: Запишем
соответствующее однородное уравнение: ![]() и
решим его.
и
решим его.
Характеристическое
уравнение ![]() ,
корни
,
корни ![]() ,
фундаментальная система решений
,
фундаментальная система решений 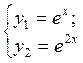 ,
общее решение
,
общее решение ![]()
Частное решение
неоднородного уравнения находим в виде: ![]()
На основе теоремы
4 запишем систему для нахождения функций ![]() :
:
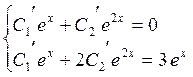 или
или 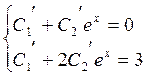 .
.
Решая систему,
найдём ![]() тогда
тогда
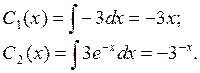
Частное решение
линейного неоднородного уравнения: ![]()
По теореме 3
запишем общее решение линейного неоднородного диф. уравнения: ![]()
Таким образом, для решения линейного неоднородного диф. уравнения необходимо вначале решить соответствующее однородное диф. уравнение, затем найти частное решение неоднородного уравнения и по теореме 3 найти общее решение неоднородного линейного диф. уравнения. При этом, если правая часть неоднородного уравнения имеет сложный вид и равна сумме функций, то для нахождения частного решения можно воспользоваться теоремой 5.
Теорема 5. Частное решение уравнения
![]()
имеет вид:
![]()
где ![]() -
частное решение уравнения
-
частное решение уравнения ![]()
![]() -
частное решение уравнения
-
частное решение уравнения ![]()
2.4 ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим уравнение
![]() , где
, где ![]() -
действительные числа.
-
действительные числа.
Общий метод
нахождения частного решения линейного неоднородного уравнения рассмотрен в п.
2.3. Однако, в уравнении с постоянными коэффициентами иногда его можно найти
более просто, не прибегая к интегрированию. Этот метод нахождения частного
решения называется методом неопределённых коэффициентов и применяется в
зависимости от вида функции ![]() .
Рассмотрим несколько случаев:
.
Рассмотрим несколько случаев:
I. ![]()
Правая часть
уравнения – многочлен ![]() -ой
степени, при этом часть коэффициентов уравнения может быть равной нулю.
Обозначим корни характеристического уравнения через
-ой
степени, при этом часть коэффициентов уравнения может быть равной нулю.
Обозначим корни характеристического уравнения через ![]() .
Частное решение уравнения в этом случае нужно искать в виде:
.
Частное решение уравнения в этом случае нужно искать в виде:
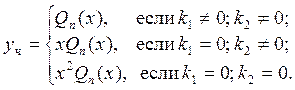
Здесь ![]() -
полный многочлен
-
полный многочлен ![]() -ой
степени с неопределёнными коэффициентами:
-ой
степени с неопределёнными коэффициентами: ![]()
Для определения
коэффициентов ![]() частное
решение подставляется в уравнение и составляется система путём приравнивания
коэффициентов справа и слева при одинаковых степенях
частное
решение подставляется в уравнение и составляется система путём приравнивания
коэффициентов справа и слева при одинаковых степенях ![]()
Пример 12. Найти общее решение
уравнения ![]()
Решение: Исходя
из теоремы 3 решим вначале соответствующее однородное уравнение: ![]() Характеристическое
уравнение
Характеристическое
уравнение ![]() его
корни
его
корни ![]() общее
решение однородного уравнения:
общее
решение однородного уравнения: ![]()
Для нахождения частного решения неоднородного уравнения применим метод неопределённых коэффициентов.
Так как ![]() ,
то форма частного решения:
,
то форма частного решения: ![]()
Дальнейшее
решение лучше вести по такой схеме. Слева за чертой записываются коэффициенты
уравнения при ![]() Умножая
на них равенства складывают с одновременным приведением подобных членов,
результат приравнивают к правой части уравнения.
Умножая
на них равенства складывают с одновременным приведением подобных членов,
результат приравнивают к правой части уравнения.
![]()
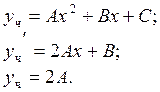
![]()
![]()
Приравнивая
коэффициенты при одинаковых степенях ![]() слева
и справа, получим систему для нахождения коэффициентов: коэффициенты при
слева
и справа, получим систему для нахождения коэффициентов: коэффициенты при ![]()
коэффициенты при ![]()
свободные члены: ![]() , решение системы:
, решение системы: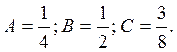
Следовательно,
частное решение неоднородного уравнения 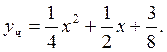
II. ![]() где
где
![]() -
многочлен
-
многочлен ![]() -ой
степени; λ – действительное число.
-ой
степени; λ – действительное число.
Обозначим корни
характеристического уравнения через ![]() .
Частное решение неоднородного уравнения в этом случае надо искать в виде:
.
Частное решение неоднородного уравнения в этом случае надо искать в виде:
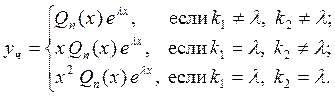
![]() -
полный многочлен
-
полный многочлен ![]() -ой
степени с неопределёнными коэффициентами, которые находятся тем же приёмом, как
и в первом случае.
-ой
степени с неопределёнными коэффициентами, которые находятся тем же приёмом, как
и в первом случае.
Пример 13. Решить уравнение ![]()
Решение: Найдём
общее решение соответствующего однородного уравнения: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.