Представим 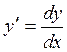 ,
тогда уравнение запишется:
,
тогда уравнение запишется: 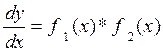 .
.
Умножим на dx : ![]() .
.
Исключив из рассмотрения точки, где f2 (y) = 0, разделим на f2 (y) :
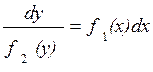 .
.
Это уравнение называется уравнением с разделёнными переменными.
Интегрируя равенство, получим:
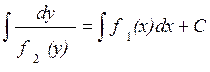 , где С –
произвольная постоянная.
, где С –
произвольная постоянная.
Это – общий интеграл уравнения, входящие в него неопределённые интегралы находятся методами, рассматриваемыми в интегральном исчислении. Если диф. уравнение записано в виде:
P(x,y)dx + Q(x,y)dy = 0, то это уравнение с разделяющимися переменными, если
P(x,y) = P1(x)*P2(y) ; Q(x,y) = Q1(x)*Q2(y)
Интегрирование уравнения проводится так:
P1(x)*P2(y) + Q1(x)*Q2(y) = 0
Считая ![]() ,
,
![]() ,
разделим на
,
разделим на ![]() :
:
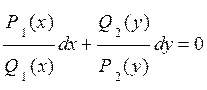 ;
;
Интегрируя:
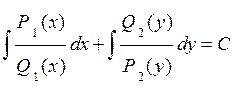
- общий интеграл уравнения.
Заметим, при разделении переменных могут быть «потерянные» решения, которые в некоторых случаях будут особыми решениями.
Пример 1. Проинтегрировать уравнение: 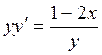 .
.
Решение: Так как уравнение можно записать в виде:
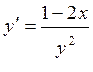 ,
то это уравнение с разделяющимися переменными. Решаем его:
,
то это уравнение с разделяющимися переменными. Решаем его:
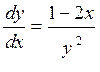 ;
;
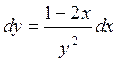 ;
;![]() ;
;
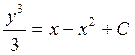 -
общий интеграл уравнения. При необходимости можно найти общее решение
уравнения:
-
общий интеграл уравнения. При необходимости можно найти общее решение
уравнения: ![]() .
.
Пример 2. Решить задачу Коши: ![]() .
.
Решение: Это –
уравнение с разделяющимися переменными. Найдём сначала общее решение уравнения,
а затем выделим частное по начальному условию. Разделим уравнение на ![]() :
:
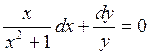 ;
;
Интегрируя: 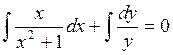 ,
получаем
,
получаем 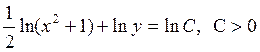 .
.
При решении диф. уравнений произвольную постоянную лучше записывать после вычисления интегралов в форме, удобной для дальнейших преобразований. Потенцируя:
![]() или
или
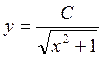 -
общее решение уравнения.
-
общее решение уравнения.
Найдём С, используя начальное условие: y=2 при х=0, тогда С=2.
Частное решение
уравнения: 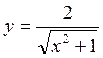 .
.
1.4 ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Если в диф.
уравнении ![]() функцию
функцию![]() можно
преобразовать к виду
можно
преобразовать к виду 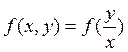 ,
то диф. уравнение называется однородным уравнением относительно х и у
(или просто однородным). Однородное уравнение решается подстановкой
,
то диф. уравнение называется однородным уравнением относительно х и у
(или просто однородным). Однородное уравнение решается подстановкой
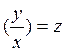 , где z=z(x) –
новая функция, приводится к диф. уравнению с разделяющимися переменными.
, где z=z(x) –
новая функция, приводится к диф. уравнению с разделяющимися переменными.
Алгоритм решения:
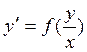 ;
;
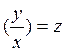 ;
y=zx ;
;
y=zx ; ![]() . Подставляя в уравнение:
. Подставляя в уравнение: ![]() ;
;
![]() ;
;
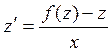 .
.
Это – уравнение с разделяющимися переменными:
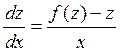 ;
;
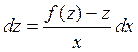 ;
;
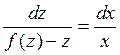 .
После интегрирования, заменив
.
После интегрирования, заменив 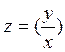 ,
получаем общий интеграл уравнения.
,
получаем общий интеграл уравнения.
Если уравнение записано в виде P(x,y)dx + Q(x,y)dy = 0, то оно будет однородным, если функции P(x,y) и Q(x,y) однородные функции одного измерения, т.е. P(tx,ty)=tn*P(x,y);
Q(tx,ty)=tn*Q(x,y).
Где n=1; 2; 3;……
Пример 3. Проинтегрировать уравнение ![]() .
.
Решение: Запишем
уравнение в виде: 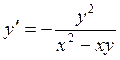 или
или
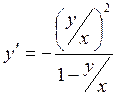 .
Это однородное уравнение относительно х и у. Замена:
.
Это однородное уравнение относительно х и у. Замена: 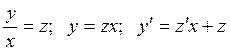 .
Подставляем в уравнение:
.
Подставляем в уравнение:
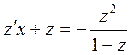 ;
;
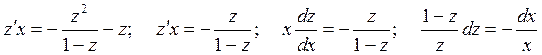 ;
;
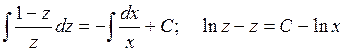 .
.
Заменяем: 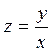 :
:
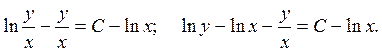
![]() -
общий интеграл уравнения.
-
общий интеграл уравнения.
1.5 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Диф. уравнение вида:
![]() , где
, где ![]() -
непрерывные функции, называется линейным однородным, если
-
непрерывные функции, называется линейным однородным, если ![]() ,
то линейным неоднородным.
,
то линейным неоднородным.
Линейное
однородное уравнение ![]() решается
как уравнение с разделяющимися переменными. В линейном неоднородном уравнении
переменные не разделяются.
решается
как уравнение с разделяющимися переменными. В линейном неоднородном уравнении
переменные не разделяются.
Заменой 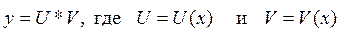 -
новые функции, оно приводится к двум уравнениям с разделяющимися переменными.
-
новые функции, оно приводится к двум уравнениям с разделяющимися переменными.
Алгоритм
решения: ![]() ;
;
![]() ;
;
![]() Подставляем
в уравнение:
Подставляем
в уравнение:
![]()
Для нахождения функций U и V запишем систему:
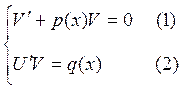
Решив уравнение
(1) (это уравнение с разделяющимися переменными), за функцию V берётся не общее решение, а любое
частное, не равное 0. Подставляя затем его в уравнение (2), находим общее
решение этого уравнения: y=φ (x,c). Общее решение линейного
неоднородного уравнения запишется в виде: ![]() .
.
Пример 4. Проинтегрировать уравнение: ![]() .
.
Решение: Это –
линейное неоднородное уравнение 1-го порядка. Заменим ![]() ;
;
![]() Подставляем
в уравнение:
Подставляем
в уравнение:
![]()
Запишем систему: 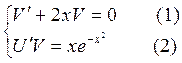 .
.
Решаем уравнение (1): 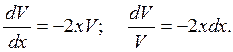
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.