Интегральное исчисление. Неопределенный интеграл. Преобразование подынтегральной функции к сумме функций

Министерство Российской Федерации

по связи и информатизации

Сибирский государственный университет телекоммуникаций и информатики

Хабаровский филиал

Методическая разработка

к тестовым заданиям по курсу «Высшая математика»

 (для студентов I курса (2 семестр) заочного факультета)

Хабаровск

2003

УДК 517

: Методическая разработка к тестовым заданиям по курсу « Высшая математика» (для студентов I курса (2 семестр) заочного         факультета).

Хабаровский филиал СибГУТИ. 2003 г.

Методическое пособие предназначено для студентов факультета заочного обучения и рассматривает вопросы по темам: интегральное исчисление, дифференциальные уравнения, элементы операционного исчисления. Приведено решение примеров по тестовым  заданиям.

Кафедра математики и физики.

Рецензент:

Утверждено Советом факультета дневного отделения от 26.03.03.

Протокол № 19 (дополнительный).

СОДЕРЖАНИЕ

                                                                                                                                  Стр.

1    Интегральное исчисление………………………………………………..………..4

1.1  Неопределенный интеграл………………………………………………………..4

1.1 .1 Преобразование подынтегральной функции к сумме функций………………5

1.1.2  Вычисление интегралов с применением компенсирующего множителя……………………………………………………………………….5

1.1.3  Вычисления интегралов путем введения функции под дифференциал…….……………………………………….…………………….7

1.1.4  Вычисление интегралов с применением формулы

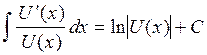…………..…………………………………………………7

1.2  Определенный интеграл…………………………………………………………..8

1.3  Интеграл с бесконечными пределами……………………………………………9

2  Дифференциальные уравнения……………..…………………………………...11

2.1  Дифференциальные уравнения первого порядка с разделяющимися переменными……………………………………………………………………..11

2.2  Однородные дифференциальные уравнения первого порядка………………..12

2.3  Линейные дифференциальные уравнения первого порядка…………………..13

2.4  Дифференциальные уравнения второго порядка, допускающие понижение порядка……………………………………………………………………………14

2.5  Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами…………………………………………………16

2.6  Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами…………………………………………………18

3  Элементы операционного исчисления……………………………………….…21

Список литературы……..……………………………………………………………..24

1 ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

1.1  Неопределенный интеграл

Определение: Функция F(x) называется первообразной функцией функции f(x), определенной на [a, b], если в каждой точке этого отрезка F’(x)=f(x).

Процесс нахождения первообразной для заданной функции f(x) называется интегрированием.

Определение: Выражение F(x)+C, где F(x) – первообразная функции f(x), С- постоянная, называется неопределенным интегралом от функции f(x) и обозначается .

Таким образом, по определению:

.

Таблица основных интегралов

1		14
2		15
3	, при n¹-1	16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

Правила интегрирования:

1 ,

2 , где С-const,

3

При интегрировании функции различными методами, в итоге, интегралы будут сводиться к одному или нескольким табличным. Рассмотрим методы интегрирования функций, которые применяются при решении текстовых заданий.

1.1.1 Преобразование подынтегральной функции к сумме функций

Пример 1.

Вычислить интеграл .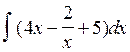

Решение:

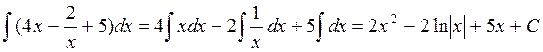
При решении использовались табличные интегралы, произвольные постоянные объединены в одну.

Пример 2.

Вычислить интеграл.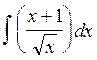

Решение:

       

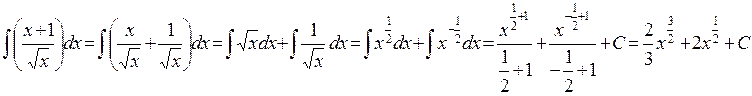
1.1.2 Вычисление интегралов с применением компенсирующего множителя

Если , то

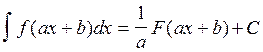, где a,b,C – const (a¹0).

Множитель  называется компенсирующим множителем.

Пример 1.

Вычислить интеграл

Решение:

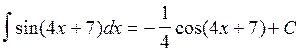, здесь а=4.

Пример 2.

Вычислить интеграл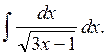      

Решение:

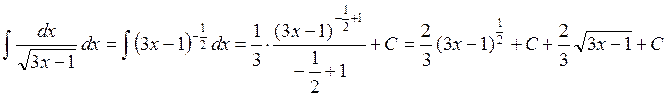
Пример 3.

Вычислить интеграл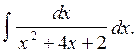 

Решение:

Легко видеть, что , следовательно

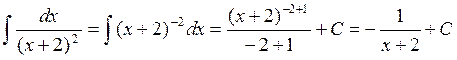
Пример 4.

Вычислить интеграл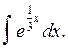 

Решение:

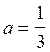
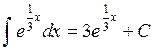
Пример 5.

Вычислить интеграл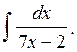

Решение:

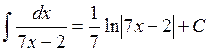
1.1.3 Вычисление интегралов путем введения функции под дифференциал

Если интеграл можно записать в виде:

 , то с учетом того, что , получим:

Если принять , и полученный интеграл совпадет с табличным интегралом, то применяется третье правило интегрирования.

Пример 1.

Вычислить интеграл

Решение:

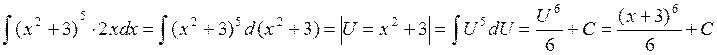
Пример 2.

Вычислить интеграл

Решение:

Здесь, поэтому, умножим и разделим интеграл на 3.

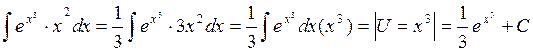
1.1.4 Вычисление интегралов с применением формулы      

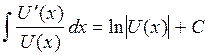
Пример 1.

Вычислить интеграл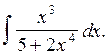

Решение:

В числителе должна стоять производная от знаменателя.

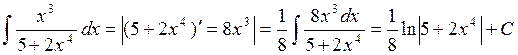
Пример 2.

Вычислить интеграл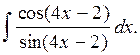

Решение:

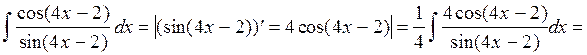½в числителе стоит производная от знаменателя½=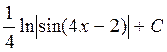

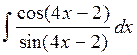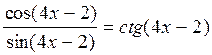Интеграл  можно вычислить еще одним способом: легко видеть, что  , следовательно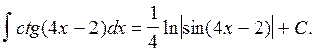

В данном примере применяли табличный интеграл (10).

1.2  Определенный интеграл

Для определенного интеграла применяется формула Ньютона – Лейбница:

Пример 1.

Вычислить интеграл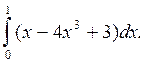  

Решение:

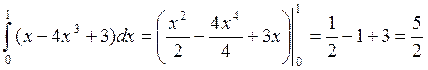
Пример 2.

Вычислить интеграл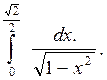

Решение:

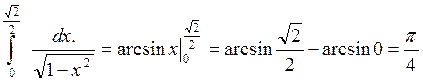
Пример 3.

Вычислить интеграл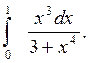

Решение:

В числителе стоит производная знаменателя, поэтому

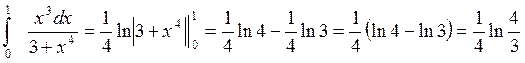
Пример 4.

Вычислить интеграл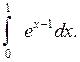

Решение:

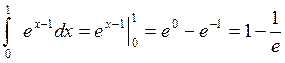
1.3  Интеграл с бесконечными пределами

Определение: Несобственным интегралом первого рода от функции f(x)

называется предел интеграла  при t®+¥ :

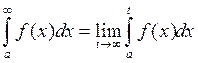
Если предел существует и конечен, то интеграл сходится. Если предел не существует или равен бесконечности, то интеграл расходится.

Аналогично определяются несобственные интегралы и для других бесконечных интервалов.

,

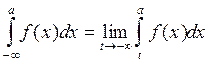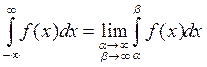
Пример 1.

Вычислить интеграл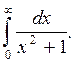

Решение:

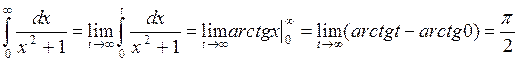
Пример 2.

Вычислить интеграл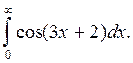

Решение:

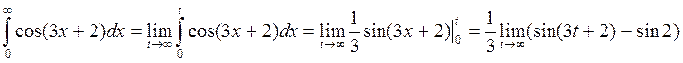
 не существует, следовательно, интеграл расходится (не существует).

Пример 3.

Вычислить интеграл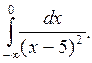 

Решение:

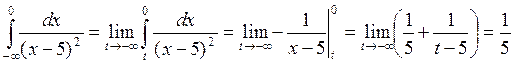
Пример 4.

Вычислить интеграл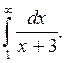

Решение:

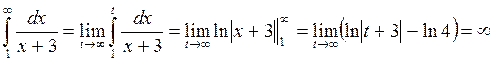
Пример 5.

Вычислить интеграл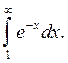

Решение:

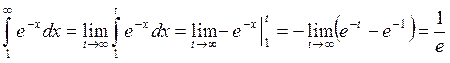
2 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

2.1 Дифференциальные уравнения первого порядка с разделяющимися             

переменными

Дифференциальные уравнения первого порядка с разделяющимися переменными имеют общий вид:

.

Интегрирование уравнения проводится следующим образом:

1)представим 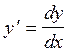, тогда уравнение запишется 

;

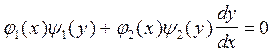2) умножим на dx, получим ,

3) разделим на : .

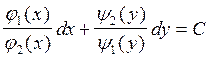Примеры дифференциальных уравнений с разделяющимися переменными:

Пример 1.

Делим обе части уравнения на xy¹0:

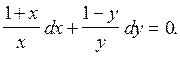 Далее интегрируем.

Пример 2.

Преобразуем уравнение:

.

Делим обе части уравнения на :

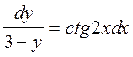
Пример 3.

Разделим на :

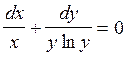
Пример 4.

Преобразуем обе части уравнения:

Разделим на 1+e^x  обе части уравнения:

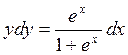
2.2 Однородные дифференциальные уравнения первого порядка

Если в дифференциальном уравнении  функцию f(x,y) можно преобразовать к виду 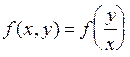, то дифференциальное уравнение называется однородным.

Однородное уравнение задается в дифференциальной форме:

.

Функции P(x,y) и Q(x,y) – однородные одинакового порядка