Интегральное исчисление функции одной переменной. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла

Министерство связи РФ

Сибирский Государственный Университет

телекоммуникаций и информатики

Хабаровский филиал

,

Интегральное исчисление функции одной переменной

(методическое пособие к контрольной работе по высшей математике)

Для студентов-заочников первого курса.

Хабаровск, 2001

УДК 517

А.А., Интегральное исчисление функции одной переменной (методическое пособие к контрольной работе по высшей математике). Для студентов-заочников первого курса. На правах рукописи.

Методическое пособие написано в соответствии с программой курса Высшая математика для студентов-заочников всех специальностей ХФ СибГУТИ. Пособие содержит основной теоретический материал, образцы решения задач, задачи для самостоятельного решения с ответами. Для углубленного изучения приведен список учебной литературы. Первая часть пособия написана А.А. , вторая часть А.Н. .

Рецензент старший преподаватель

Утверждено Советом заочного факультета протокол №_____ от _____

Хабаровский филиал СибГУТИ

Хабаровск, 2001

Перед изучением данной темы необходимо повторить правила и формулы дифференцирования функции одной переменной

Часть I. Неопределенный интеграл

§ 1.1 Первообразная и неопределенный интеграл

В дифференциальном исчислении основной задачей является нахождение от заданной функции  ее производной  или дифференциала

Обратная задача, состоящая в определении функции  по ее известной производной  или дифференциалу , представляет собой основную задачу интегрального исчисления.

Определение. Функция  называется первообразной функцией функции , определенной на отрезке , если в каждой точке этого отрезка  или .

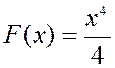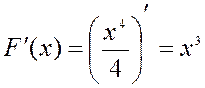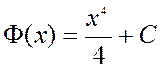Процесс нахождения первообразной для заданной функции  называется интегрированием. Очевидно, что действия дифференцирование и интегрирование являются взаимно обратными. Заметим, если, например, , то ее первообразная , так как . В то же время функция , где  - произвольная постоянная, так же является первообразной для , так как 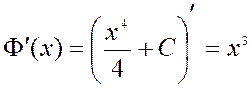. Это свойство имеет место и в общем случае.

Теорема. Если  и  две первообразные функции  на отрезке , то во всех точках этого отрезка , где  – произвольная постоянная величина.

Из теоремы следует, что если известна одна первообразная функция  для данной функции , то все множество первообразных функции  запишется в виде , где  – произвольная постоянная.

Определение. Выражение ,  – первообразная функции ,  - произвольная постоянная, называется неопределенным интегралом от функции  и обозначается символом .

Здесь знак  – знак интеграла,  – подынтегральная функция,  – подынтегральное выражение,  – переменная интегрирования.

Таким образом, по определению:

=, где

Наличие произвольной постоянной величины  объясняет, почему  называется неопределенным. Заметим, подынтегральное выражение есть дифференциал первообразной функции, т.е. .

Любая ли функция  имеет первообразную?

Ответ на этот вопрос дает основная теорема интегрального исчисления (теорема Коши).

Теорема. Если функция  непрерывна на отрезке, она имеет непрерывную первообразную функцию.

§ 1.2 Свойства неопределенного интеграла. Таблица интегралов

Из определения неопределенного интеграла следуют два его свойства:

1. 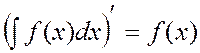 или

2.  или

3. Интеграл от суммы (первое правило интегрирования):

4. О вынесении постоянного множителя (второе правило интегрирования):

=, где

5. Третье правило интегрирования: формула интегрирования сохраняет свой вид при замене переменной интегрирования любой дифференцируемой функцией от нее: если =,  - дифференцируемая функция, то справедливо равенство =.

Запишем таблицу основных интегралов. Так как действия дифференцирования и интегрирования являются взаимно обратными, то простейшую таблицу интегралов можно получить обращением таблицы производных. Дополним эту таблицу интегралами, наиболее часто встречающимися на практике. Заметим, результат интегрирования всегда можно проверить дифференцированием: если =, то .

Таблица 1.1 Таблица основных интегралов

№ п/п	Интеграл	№ п/п	Интеграл
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

Приведенные в таблице интегралы назовем табличными, их необходимо знать наизусть. При интегрировании функций разными методами в конечном итоге интегралы всегда будут приводиться к одному или нескольким табличным. Рассмотрим методы интегрирования функций.

§1.3 Метод непосредственного интегрирования

Под таким названием объединяются способы приведения интеграла к одному или нескольким табличным с помощью тождественных преобразований подынтегральной функции. Рассмотрим несколько таких преобразований на примерах.

1.3.1 Преобразование подынтегральной функции к сумме функций

Задача 1. Найдите интегралы:

1.

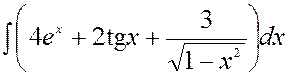
2.

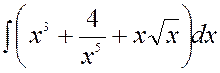
Решение. l В этих примерах подынтегральные функции записаны в виде алгебраических сумм функций, поэтому для нахождения интегралов применим первое и второе правило интегрирования и табличные интегралы.

1. == =––.

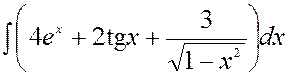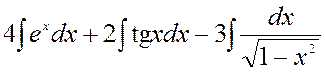Применялись (5), (8), (21) табличные интегралы, произвольные постоянные объединены в одну.

2. ==++ ++=–

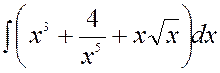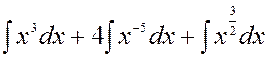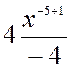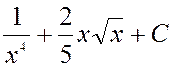
Применялся (2) табличный интеграл при значениях