Глава 2.
Функции многих переменных.
2.1. Векторная функция скалярного аргумента.
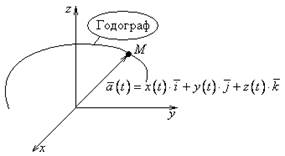 Определение:
Определение:
![]()
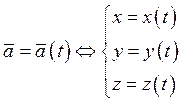
Определение предела:
![]()
![]()
![]()
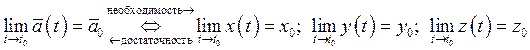
Необходимость:
![]()
Достаточность:
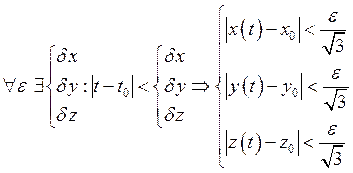
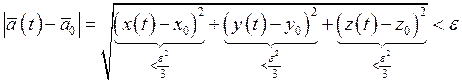
Непрерывность:
![]() непрерывна в точке
непрерывна в точке ![]()
![]()
![]()
![]() непрерывна в точке
непрерывна в точке 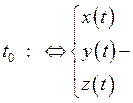 непрерывны
в точке
непрерывны
в точке ![]()
СДЕЛАТЬ ДОМА
Производная вектора функций.
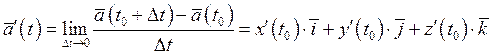
Геометрический смысл производной вектора функций.
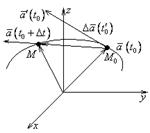
![]()
Уравнение касательной:
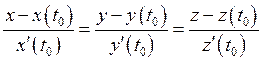
Уравнение нормали:
![]()
Правила дифференцирования вектора функций.
![]() скалярная форма.
скалярная форма.
![]() векторная форма.
векторная форма.
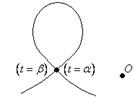
![]()
![]()
![]()
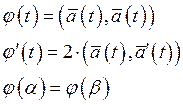
По теореме Ролля: ![]()
Тогда ![]()
Обобщение на n-мерное пространство.
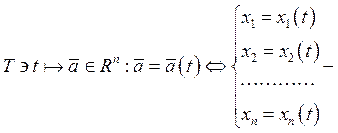 линия в
линия в ![]() мерном
пространстве.
мерном
пространстве.
Уравнение прямой в![]()
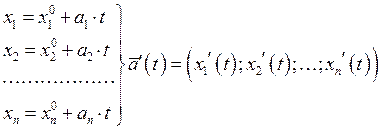
2.2. n-мерное Евклидово пространство. ![]()
![]() точка
точка
![]() вектор
вектор
![]()
![]()
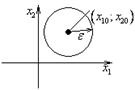
Окрестность в n-мерном пространстве.
![]()
![]()
![]()
![]()
![]()
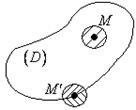
![]() область.
область.
Точка ![]() называется
внутренней точкой области если она принадлежит области, вместе со своей
окрестностью.
называется
внутренней точкой области если она принадлежит области, вместе со своей
окрестностью.
Точка ![]() называется
граничной точкой области если в любой её окрестности есть, точки, которые
принадлежат области и не принадлежат области.
называется
граничной точкой области если в любой её окрестности есть, точки, которые
принадлежат области и не принадлежат области.
Область состоящая из внутренних точек называется открытой, из граничных называется закрытой.
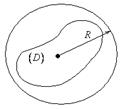
![]() ограничена,
если внутри которой содержаться все точки области.
ограничена,
если внутри которой содержаться все точки области.
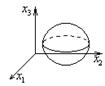
![]() сфера
радиуса
сфера
радиуса ![]()
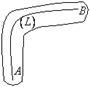
Область ![]() называется
связной, если любые две точки этой области можно соединить непрерывной кривой
целиком принадлежащей этой области, в противном случае называется не связная.
называется
связной, если любые две точки этой области можно соединить непрерывной кривой
целиком принадлежащей этой области, в противном случае называется не связная.
2.3. Функция многих (n) переменных.
![]()
![]()
![]()
Геометрический смысл функции 2-ух переменных.
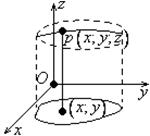
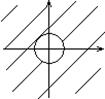
Пример:
![]()
![]()
Неограниченная, связанная, открытая.
Предел.
![]()
![]()
![]()
По Гейне: ![]()
Пример:
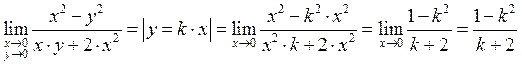
Непрерывность:
![]() непрерывна
в точке
непрерывна
в точке ![]()
![]()
На языке приращений: ![]()
![]()
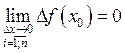
Непрерывность сложной функции многих переменных.
![]()
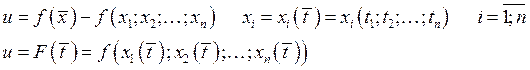
Теорема о непрерывности сложных функций.
![]() непрерывна
в точке
непрерывна
в точке ![]()
![]() непрерывна
в точке
непрерывна
в точке ![]()
![]() непрерывна
в точке
непрерывна
в точке ![]()
![]()
![]()
2.4. Свойства функций непрерывных в области.
![]() Первая теорема Вейерштрасса.
Первая теорема Вейерштрасса.
![]() непрерывна
в замкнутой ограниченной области
непрерывна
в замкнутой ограниченной области ![]()
Вторая теорема Вейерштрасса.![]()
![]()
![]() непрерывна
в замкнутой ограниченной области
непрерывна
в замкнутой ограниченной области ![]() она достигает в этой
области своих наибольших и наименьших значений.
она достигает в этой
области своих наибольших и наименьших значений.
СДЕЛАТЬ ДОМА
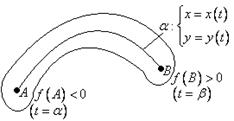
![]() Первая теорема Больцано-Коши.
Первая теорема Больцано-Коши.
![]()
![]() непрерывна
в связной области
непрерывна
в связной области ![]()
![]()
![]() точки области
точки области ![]()
![]()
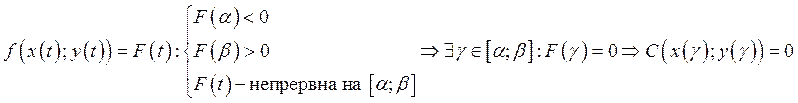 Вторая
теорема Больцано-Коши.
Вторая
теорема Больцано-Коши.
СДЕЛАТЬ ДОМА
2.5. Частная производная.
Для одной переменной.
![]() полное
приращение функции
полное
приращение функции ![]() в точке
в точке ![]()
![]()
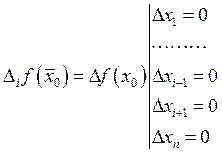
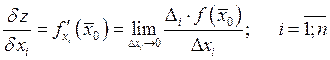
Для двух переменных.
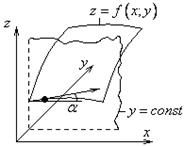
![]()
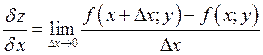
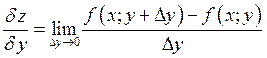
![]()
Пример:
![]()
2.6. Дифференцируемость функций многих переменных.
![]() дифференцируема
в точке
дифференцируема
в точке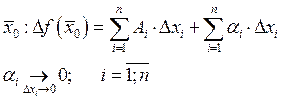
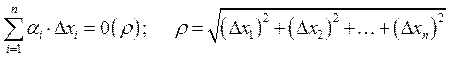
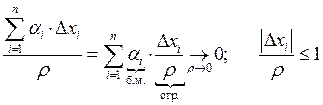
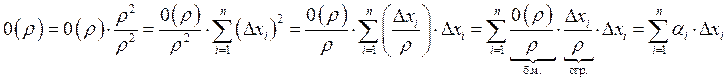
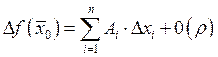
Свойства дифференцируемости функций.
![]()
![]()
![]() дифференцируема в точке
дифференцируема в точке ![]() непрерывна в точке
непрерывна в точке ![]()
СДЕЛАТЬ ДОМА
![]() Необходимое условие
дифференцирования.
Необходимое условие
дифференцирования.
![]()
![]() дифференцируема
в точке
дифференцируема
в точке ![]()
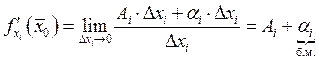
Следствие:
![]()
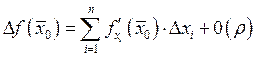
Достаточное условие дифференцируемости.
![]()
![]() непрерывна
в точке
непрерывна
в точке ![]() дифференцируема в точке
дифференцируема в точке ![]()
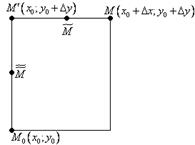 Для
двух переменных:
Для
двух переменных:
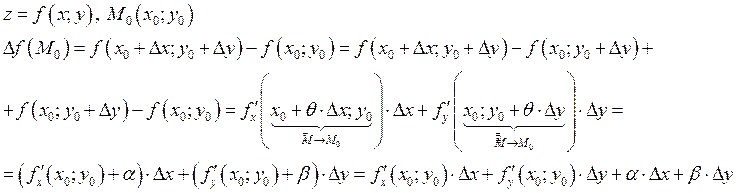
![]()
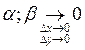
Дифференциал сложной функции.
![]()
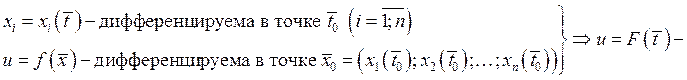 дифференцируема
в точке
дифференцируема
в точке ![]()
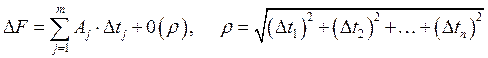
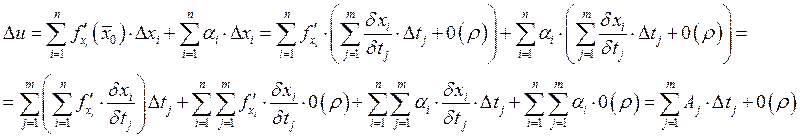
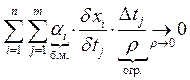
Следствие:
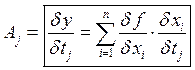
Пример:
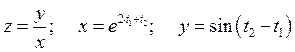
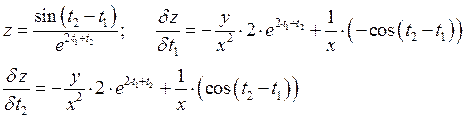
Полная производная.
![]()
![]()
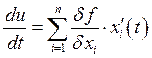
Производная определителя.
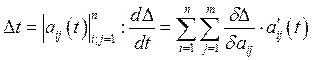
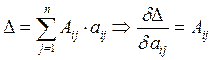
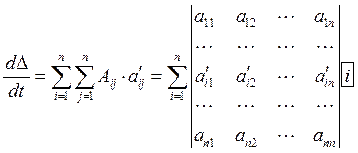
Пример:
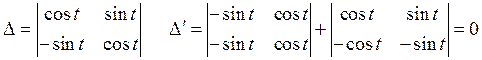
Производная неявной функции.
![]()
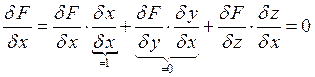
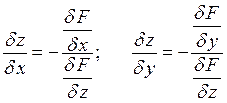
Пример:
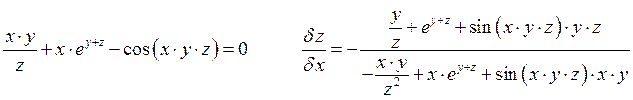
2.7. Дифференциал.
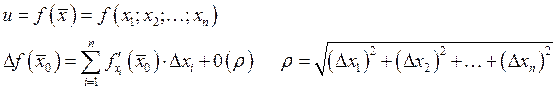
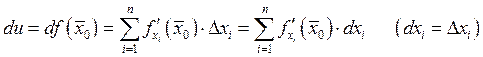
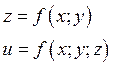 Написать
дифференциал СДЕЛАТЬ ДОМА
Написать
дифференциал СДЕЛАТЬ ДОМА
Свойства полного дифференциала.
![]()
![]()
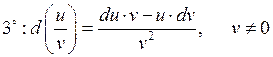
Дифференциал сложной функции. Инвариантность формы первого дифференциала.
![]()
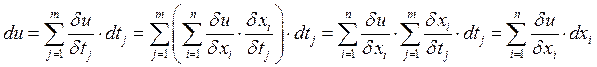
Приложение полного дифференциала.
А) Приближенное вычисление.
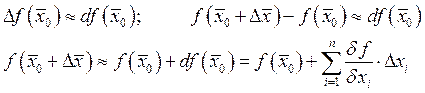
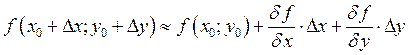
Пример:
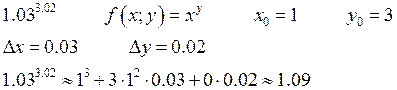
Б) Оценка погрешности.
![]()
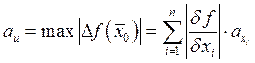
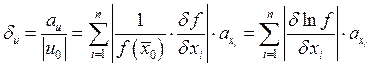
2.8. Уравнение касательной плоскости и нормали поверхности.
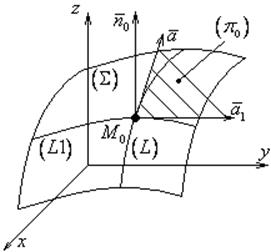
![]()
![]()
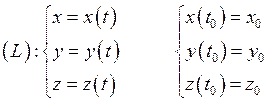
![]()
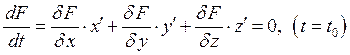
![]()
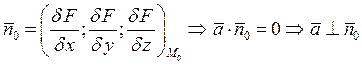
Уравнение касательной:
![]()
Уравнение нормали:
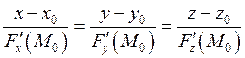
![]()
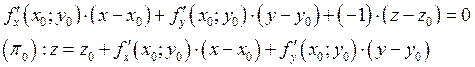
Пример:
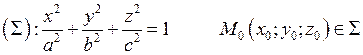
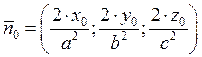
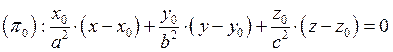
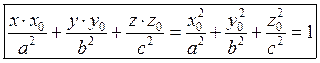
Геометрический смысл полного дифференциала функции 2-ух переменных.
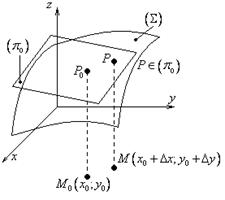
![]()

2.9. Частные производные и дифференциалы высших порядков.
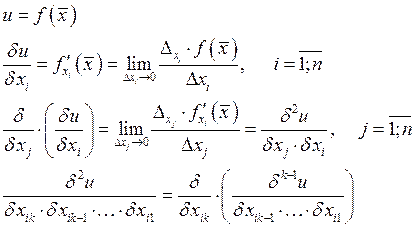
Пример:
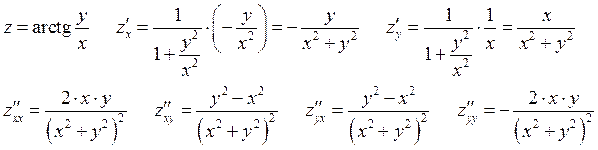
Теорема о равенствах смешанных производных.
![]() В
В ![]()
![]() непрерывны в точке
непрерывны в точке ![]()
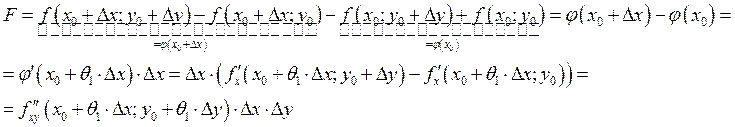
![]()
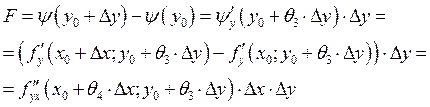
![]()
Пусть ![]()
Рассмотрим:
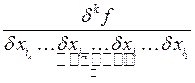
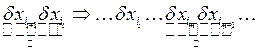
Дифференциал высших порядков.
![]()
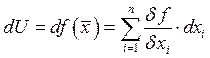
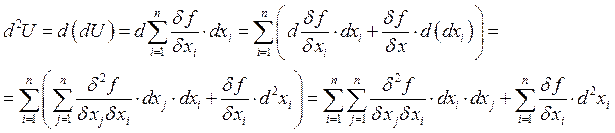
![]() неизвестная переменная:
неизвестная переменная: ![]()
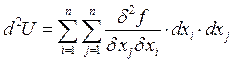
Исключение:
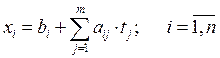
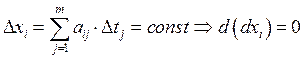
Оператор дифференцирования для функций n-переменных.
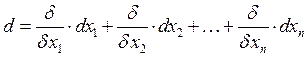
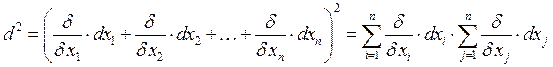
![]() независимая переменная:
независимая переменная: 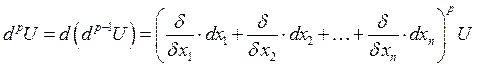
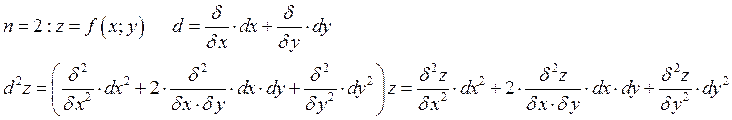
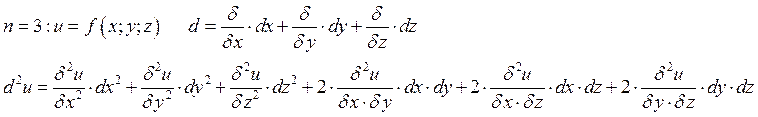
2.10. Формула Тейлора функции n-переменных.
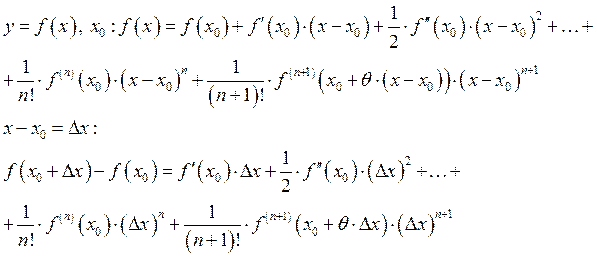
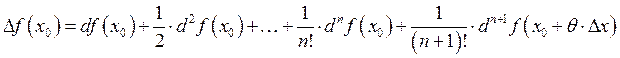
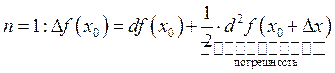
Функции n-переменных.
![]()
![]() дифференцируется
дифференцируется ![]() раз в
раз в ![]()
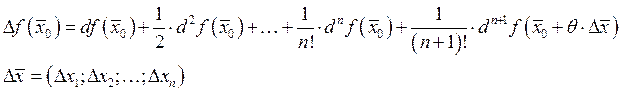
![]()
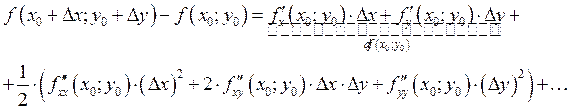
2.11. Локальный экстремум функции многих переменных.
![]()
Определение:
![]() точка локального
точка локального ![]() строгий экстремум.
строгий экстремум.
Пример:
![]() точка локального
точка локального ![]()
![]() Необходимое условие
локального экстремума.
Необходимое условие
локального экстремума.
![]()
![]() дифференцируема в точке
дифференцируема в точке ![]() локальный экстремум
локальный экстремум ![]()
![]() локальный
локальный ![]()
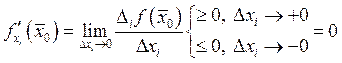
Следствие: ![]()
![]() Достаточное условие
локального экстремума.
Достаточное условие
локального экстремума.
![]()
![]() дифференцируема
2 раза в
дифференцируема
2 раза в ![]() точка локального
точка локального ![]()
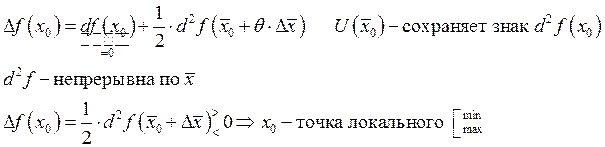
2.12. Исследование знака 2-ого дифференциала.
Критерии Сильвестра.
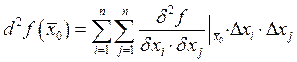
Квадратичная форма: 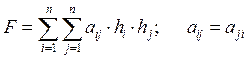
![]()
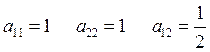
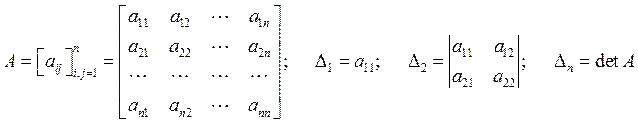
Критерий Сильвестра: ![]() главные
миноры.
главные
миноры.
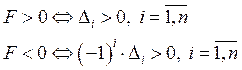
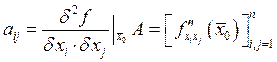
![]()
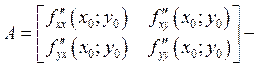 матрица вторых производных.
матрица вторых производных.
![]() точка
точка ![]()
![]() точка
точка ![]()
Пример:
![]()
![]() Необходимое условие:
Необходимое условие:
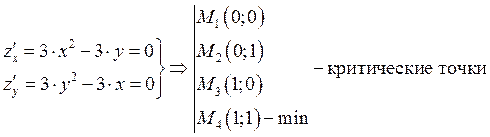
![]() Достаточное условие:
Достаточное условие:
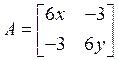
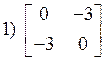
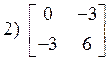
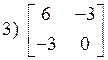
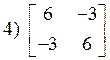
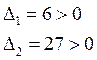
2.13. Условный экстремум функции многих переменных.
![]()
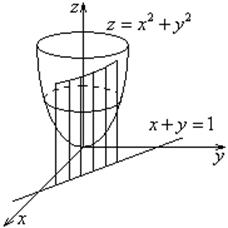 Пример:
Пример:
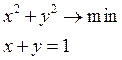
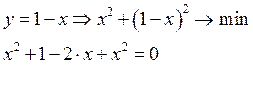
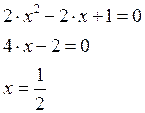
Метод неопределённого множителя Лагранжа.
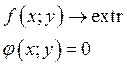
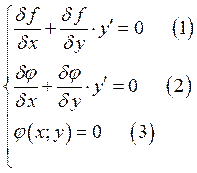
Домножим ![]() на
на ![]() и сложим
и сложим ![]() и
и ![]()
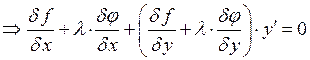
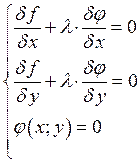 , Введём
, Введём ![]()
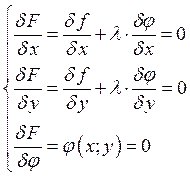
Метод неопределённых множителей Лагранжа для функций n-переменных.
Задача:
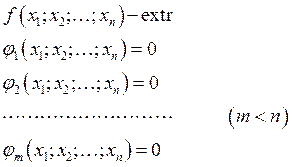
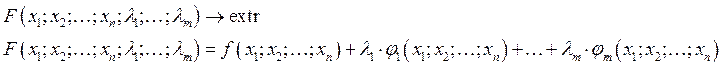
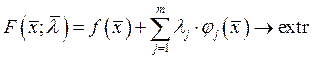
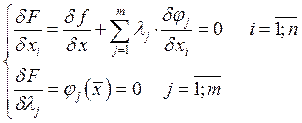
Пример 1:
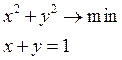
![]()
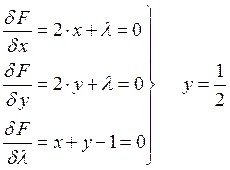
Пример 2:
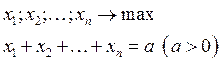
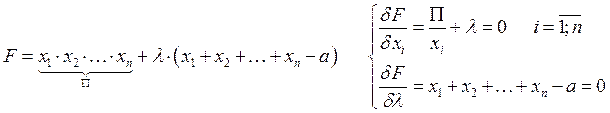
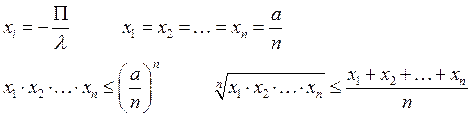
Наибольшее и наименьшее значение функции в области 2-ух переменных.
![]()
![]() замкнутая
и ограниченная область.
замкнутая
и ограниченная область.
![]() Критические точки
Критические точки ![]()
![]() Поведение функции на границе.
Поведение функции на границе.
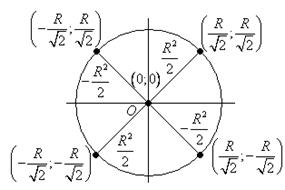 Пример:
Пример:
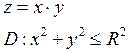
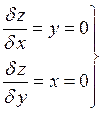
![]()
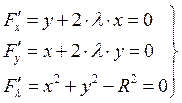 исключив
исключив ![]() из 1-ого и 2-ого уравнения,
подставим его в 3-ее.
из 1-ого и 2-ого уравнения,
подставим его в 3-ее.
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.