Свойства дискретных функций Уолша. Свойство мультипликативности. Дискретное прямое и обратное преобразование Уолша

Свойства дискретных функций Уолша

1)  Свойство мультипликативности

2)  Свойство симметрии:

3)  Свойство ортогональности:

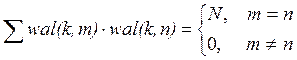
4)  Дискретное прямое и обратное преобразование Уолша

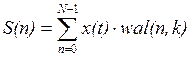
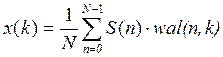
5)  Свойство периодичности:

6)  Теорема запаздывания

Для Фурье:

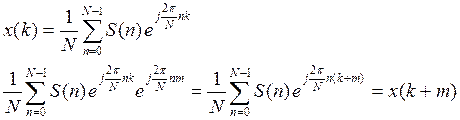
Для Уолша:

  

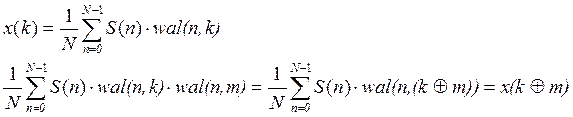
7)  Сдвиг идет на  этот сдвиг называется диадным.

С понятие сдвига функции сталкиваемся тогда, когда вычисляем КФ, а с теоремой запаздывания, когда вычисляем свертку двух функций.

Для Фурье преобразования имеет место арифметический сдвиг – параллельный перенос сигналов по оси времени. Для преобразования Уолша сдвиг уже оказывается неарифметическим, а диадным.

Диадный сдвиг характерен если  , это приводит к перестановке отсчетов внутри последовательности, а арифметический сдвиг выводит частоту отсчетов за пределы рассматриваемой области. Основное преимущество ДПУ по сравнению с ДПФ заключается в том, что при этих вычислениях отсчеты сигнала  на  , исключаются операции умножения. Для ДПФ надо  на комплексное число (а это два числа причем каждое число представляется большим количеством разрядов), а все это замедляет процесс обработки.

По аналогии с БПФ можно построить БПУ – это способ организации вычислений, их уравнения похожи. Нужно вычислить всего  операций суммирования.

Невыполнение т. Запаздывания ведет к тому, что спектральное преобразование Уолша не удается использовать при согласованной фильтрации, т. к. нет инвариантности к сдвигу сигнала во времени, но преимущества в скорости и удобстве вычислений способствует широкому испоьзованию преобразований Уолша:

ü  Обработка и передача изображений

ü  Распознавание образов

ü  Сжатие данных

Обработка сигналов во временной области. Цифровая фильтрация.

Линейные дискретные и цифровые фильтры

Дискретный фильтр – устройство выполняющее следующую операцию:

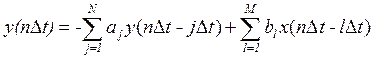 или

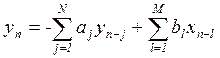 - (1)                           разностное уравнение.

- выходной сигнал

 - входной сигнал.

Разностное уравнение описывает алгоритм работы ЦФ. Если  и  зависят от текущего индекса  , но не зависит от значений  и  то фильтр и разностное уравнение линейны, если вдобавок  и  = const, то фильтр инвариантен во времени, а разностное уравнение является уравнением с постоянными коэффициентами. Для вычисления   в соответствии с формулой надо задать начальные условия:

, а для  начальные условия могут быть нулевыми.

Из (1) видно, что для вычисления надо выполнить:

ü  Задержку (запоминание)

ü  Операцию умножения

ü  Операцию алгебраического сложения

Реализация выражения (1) с малыми ошибками не зависящими от температуры, влажности, времени и т.д. возможна с помощью цифрового устройства.

В ЦФ входной и выходной сигналы цифровые (представлены двоичным кодом) и коэффициенты  и  тоже цифровые. Но т.к. цифровое представление выполняется с помощью ограниченного числа разрядов, то вычисления проводятся с погрешностью, ЦФ – нелинейные устройства и к ним не применимы методы анализа и синтеза линейных систем, но обычно число разрядов велико и погрешностью представления можно пренебречь, т.е. считают, что все числа представляются точно. Неточность учитывается только при оценивании точности цифровых фильтров.

Фильтры бывают рекурсивными и не рекурсивными.

Если в разностном уравнении хотя бы один , то это рекурсивный фильтр, если все , то это не рекурсивный фильтр. Рекурсивный фильтр – устройство с обратной связью, а не рекурсивный без нее. Иногда не рекурсивный фильтр называют КИХ-фильтром, а рекурсивный – БИХ-фильтром.

Анализ свойств дискретных фильтров ведется с помощью - преобразования. Это аналог аналог преобразования Лапласа в теории аналоговых фильтров.

Свойства Z-преобразования:

1) 

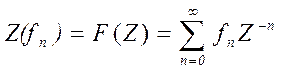
РИСУНОК СИГНАЛА

    

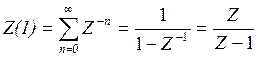
2)  Свойство линейности:

3)  Теорема сдвига:

4)  Обратное Z-преобразование:

  

Передаточные функции фильтров

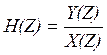
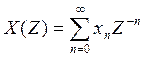 - Z-преобразование входного сигнала

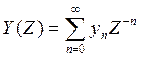 - Z-преобазование выходного сигнала

Если к разностному уравнению применить Z-преобазование, то в общем виде для рекурсивного фильтра получим:

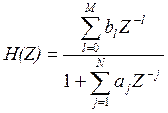, для не рекурсивного фильтра все

Использование передаточных функций облегчает анализ и синтез структурных схем фильтров.

Структурные схемы дискретных фильтров  

Данные схемы существуют в двух формах, которые описываются одним и тем же разностным уравнением:

1)  Прямая форма реализации рекурсивного фильтра (на основе разностного уравнения)

РИСУНОК ФИЛЬТРА

В схемах присутствуют элементы трех типов:

ü  N+M – элементов задержки (представляющие собой регистр)

ü  N+M+1 – умножителей

ü  N+M+1 – сумматоров

Период следования входных и выходных отсчетов  равен , т.е. интервалу дискретизации синала.

2)  Каноническая форма рекурсивного фильтра:

 где

                                         

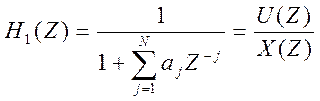
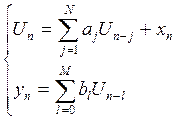
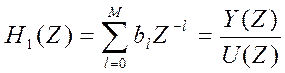
РИСУНОК ФИЛЬТРА

Здесь меньше элементов задержки: .