Глава 1.
Интегралы.
1.1. Первообразная и неопределённый интеграл.
![]() называется первообразной функции
называется первообразной функции ![]() на интервале
на интервале ![]() если:
если: ![]()
Свойства.
![]()
![]() первообразная
от
первообразная
от ![]()
![]()
![]()
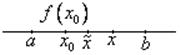 По теореме Лагранжа:
По теореме Лагранжа: 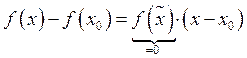
Следствие: ![]()
![]()
![]() первообразной
от
первообразной
от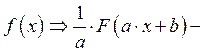 первообразная от
первообразная от ![]()
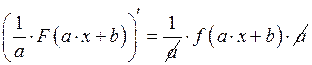
Неопределённый интеграл.
![]()
![]() подынтегральная функция.
подынтегральная функция.
![]() подынтегральное выражение.
подынтегральное выражение.
Свойства.
![]()
![]()
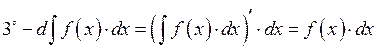
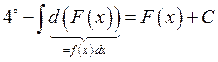
1.2. Таблица интегралов.
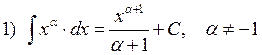
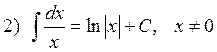
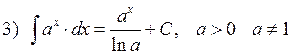
![]()
![]()
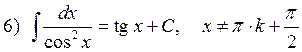
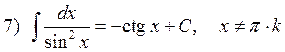
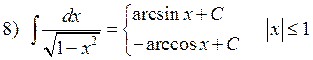
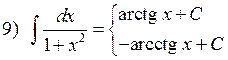
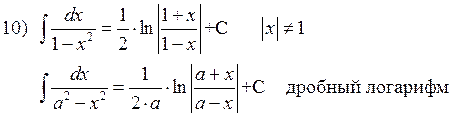
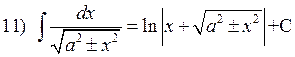
![]()
![]()
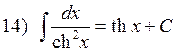
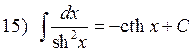
1.3. Методы интегрирования.
А. Метод замены переменной.
![]()
![]()
Пример 1: 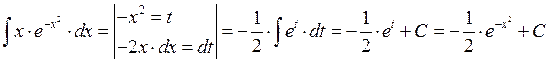
Пример 2: 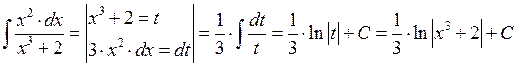
Пример 3: 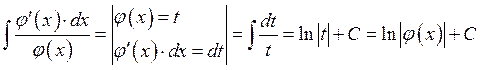
Пример 4: 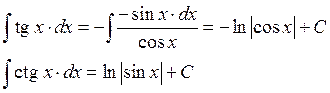
Б. Интегрирование по частям.
![]()
![]()
![]()
Пример 1: 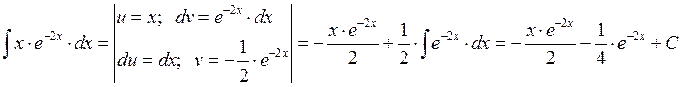
Пример 2: 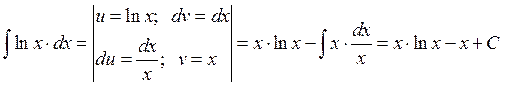
Пример 3: 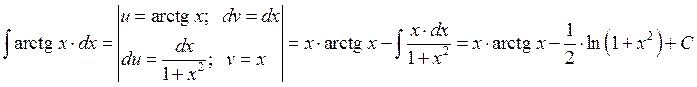
Пример 4: 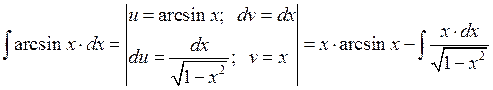
В. Метод неопределённых коэффициентов.
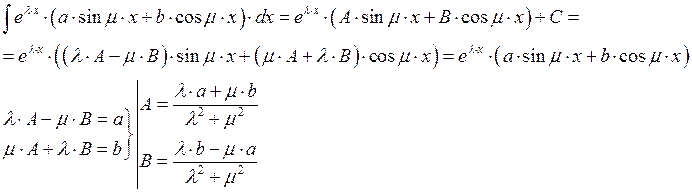
1.4. Комплексные числа и действия над ними.
![]()
![]()
![]()
![]()
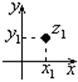
![]()
![]()
![]()
![]()
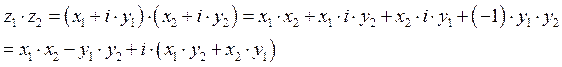
![]()
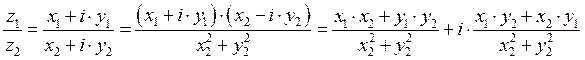
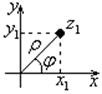
Тригонометрическая форма комплексного числа.
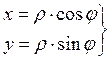
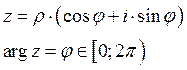
![]()
![]()
![]()
![]()
![]()
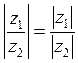
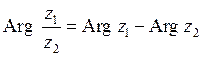
Показательная форма комплексного числа.
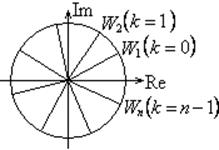
![]()
![]()
![]()
![]()
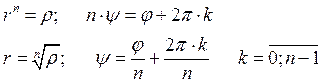
![]()
![]()
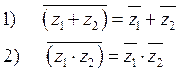
СДЕЛАТЬ ДОМА
Следствие: ![]()
1.5. Многочлен. Разложение многочлена на множители.
![]()
![]() корень
корень ![]()
Любой многочлен степени не ниже первой имеет один корень действительный или мнимый.
![]()
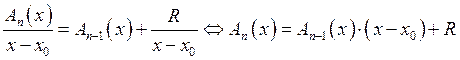
(Безу) ![]() корень
корень ![]()
Любой многочлен ![]() степени имеет ровно
степени имеет ровно ![]() корней (действительных, комплексных…)
корней (действительных, комплексных…)
![]()
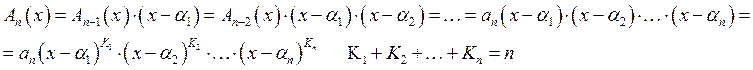
![]() корень
корень ![]()
![]() корень
корень ![]()
![]()
![]()
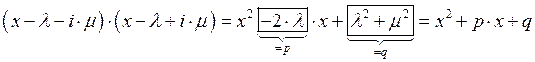
![]()
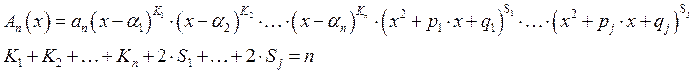
![]() корень
корень ![]() кратности
кратности ![]()
![]()
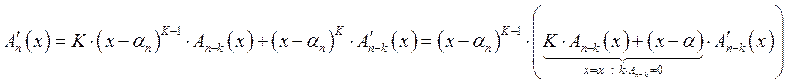
![]() корень
корень ![]() кратности
кратности
![]()
1.6. Рациональные дроби. Разложение на простейшие.
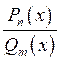
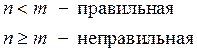
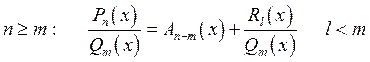
Пример: 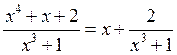
Разложение правильной рациональной дроби на простейшие.
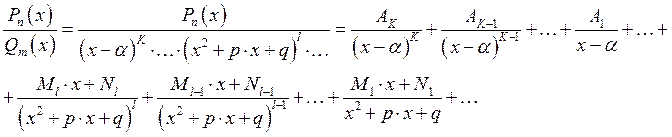
![]()
Пример 1:
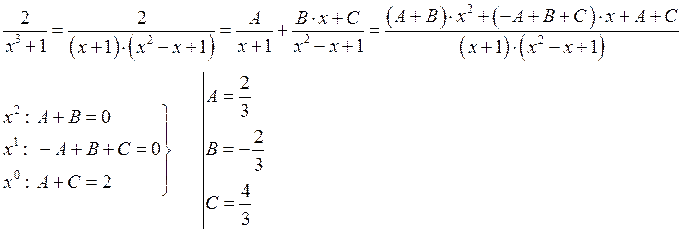
Пример 2:
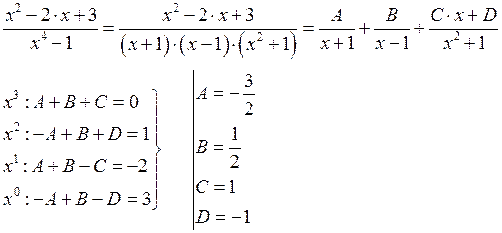
Интегрирование простейших дробей.
![]()
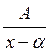
![]()
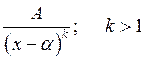
![]()
![]()
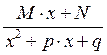
![]()
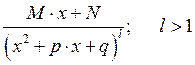
Любая дробно-рациональная функция (рациональная дробь), интегрируема в элементарных функциях.
![]()
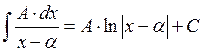
![]()
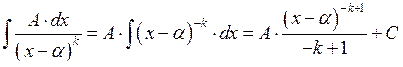
![]()
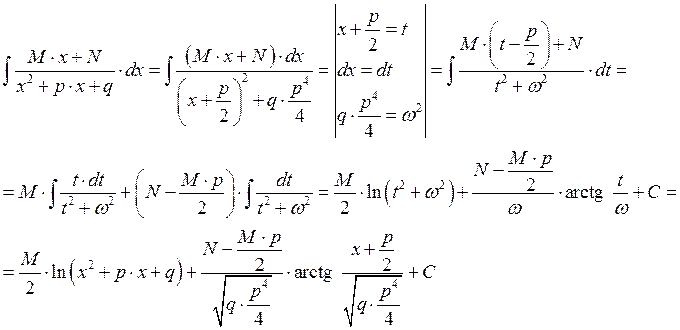
![]()
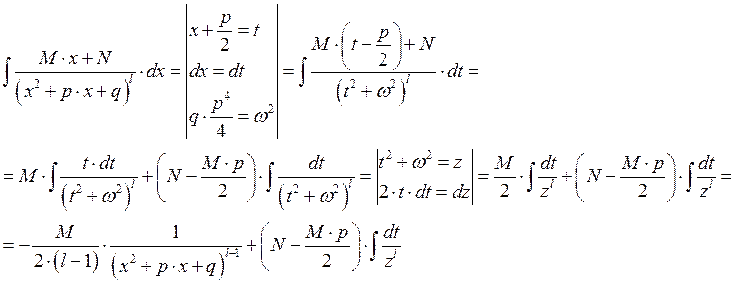
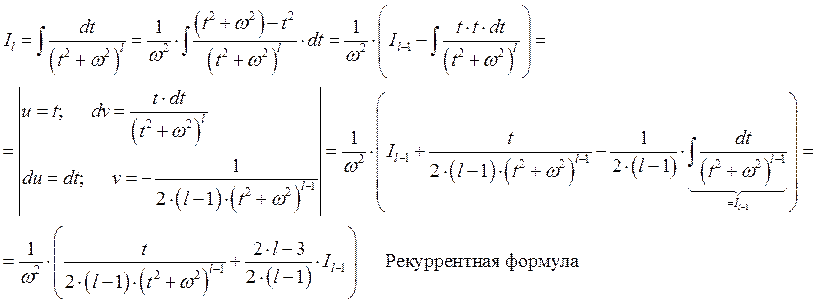 Пример:
Пример:
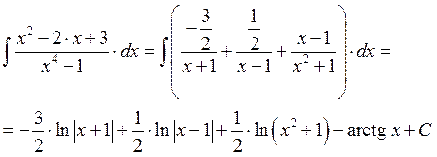
1.7. Интегрирование тригонометрических выражений.
A) ![]() а)
Пусть
а)
Пусть ![]() или
или ![]() нечётно:
нечётно:
![]()
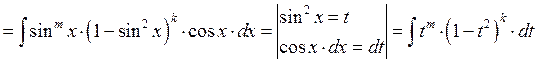
![]()
СДЕЛАТЬ ДОМА
б) Пусть ![]() или
или
![]() чётно:
чётно: ![]()
![]()
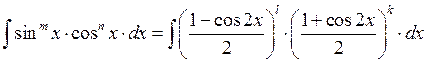
Пример:
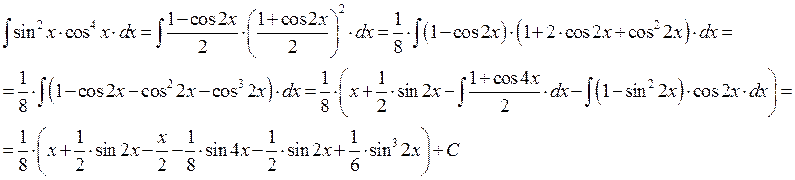 Б) Рекуррентные
формулы интегрирования.
Б) Рекуррентные
формулы интегрирования.
а) ![]()
![]()
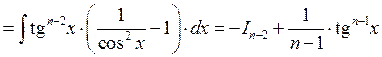
б) ![]() СДЕЛАТЬ
ДОМА
СДЕЛАТЬ
ДОМА
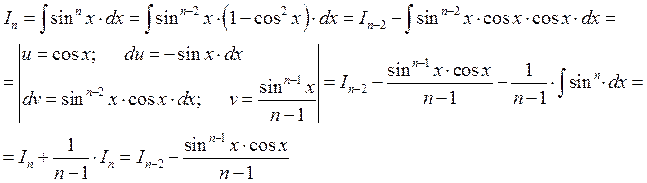
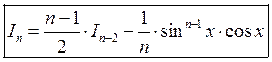
г) ![]() СДЕЛАТЬ
ДОМА
СДЕЛАТЬ
ДОМА
Пример:
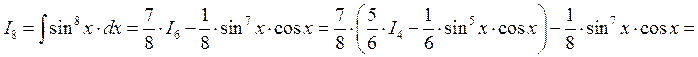 СДЕЛАТЬ
ДОМА
СДЕЛАТЬ
ДОМА
В)
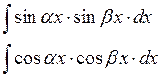
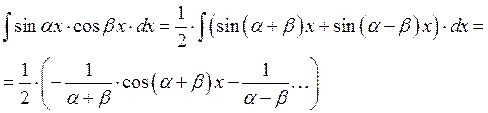
Г) Универсальная тригонометрическая подстановка.
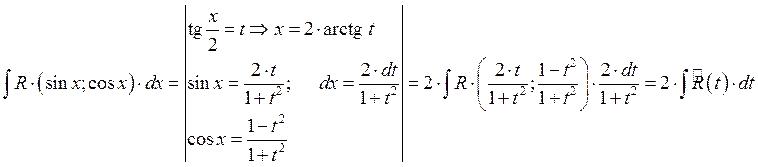
![]() рациональная функция.
рациональная функция.
Пример:
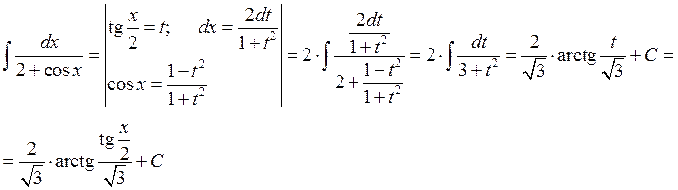
Д) Частный случай универсальной тригонометрической подстановки.
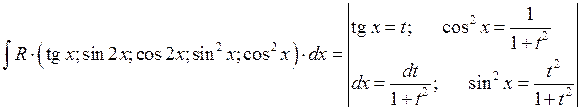
1.8. Интегрирование иррациональных выражений.
А) Приведение к рациональным функциям.
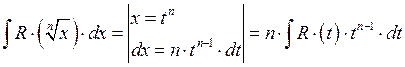
Пример:
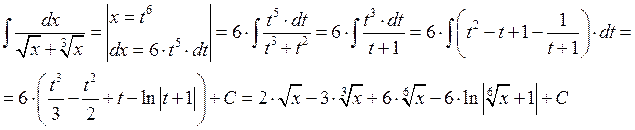
Б) Интегрирование дробно-линейной иррациональности.
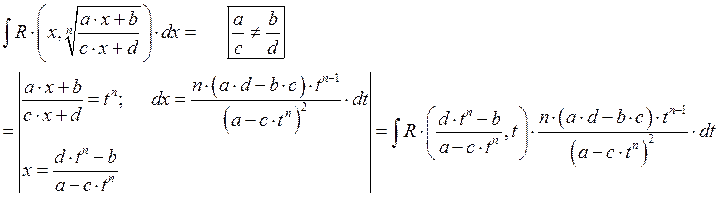
Пример:
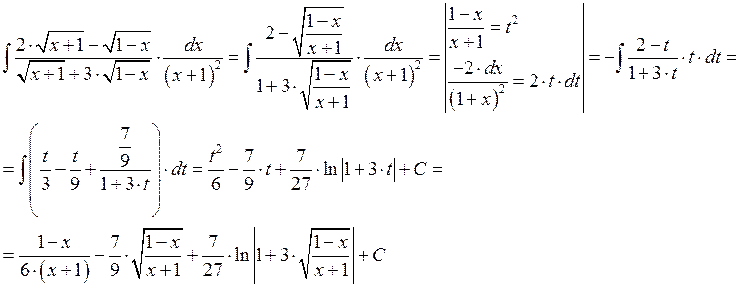
В) Интегрирование иррационального многочлена.
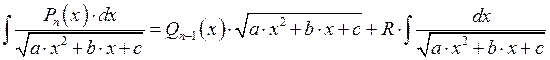
Возьмём производную от обеих частей:
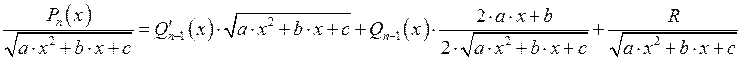
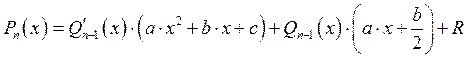
Пример:
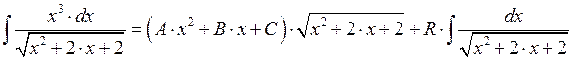
Найдём производную и помножим на знаменатель обе части:
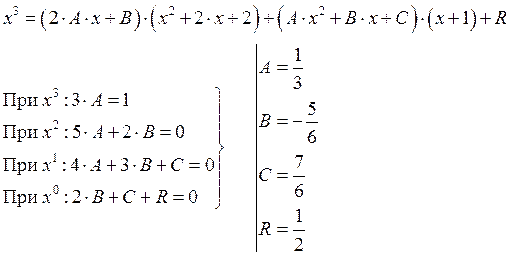
Тогда:
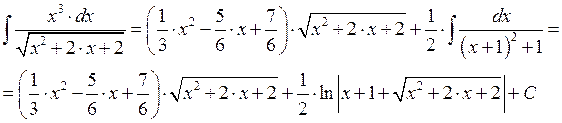
Г)
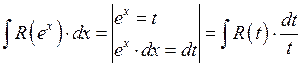
1.9. Задача, приводящая к понятию определённого интеграла (Интегралу Римана).
Задача: Площадь криволинейной трапеции.
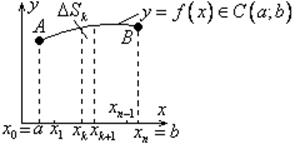
![]()
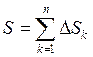
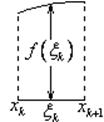
![]()
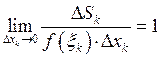
![]()
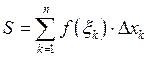
![]()
Предел не зависит от выбора ![]() и не
зависит от
и не
зависит от ![]() :
:
![]()
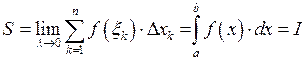
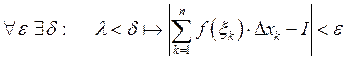
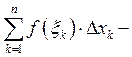 интегральная сумма.
интегральная сумма.
![]() интегральная функция.
интегральная функция.
Теорема существования определённого интеграла.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то интеграл от неё на этом отрезке
существует.
, то интеграл от неё на этом отрезке
существует.
Пример:
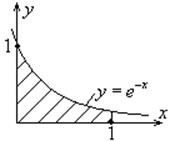
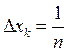
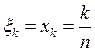
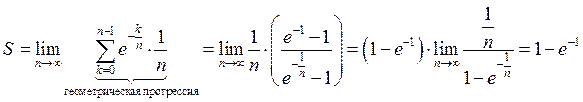
1.10. Свойства определённого интеграла.
![]()
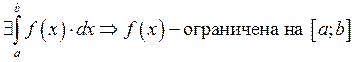
![]()
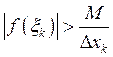
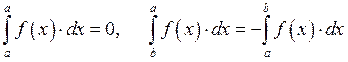
Свойства определённого интеграла.
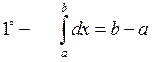
![]() Свойство линейности
Свойство линейности
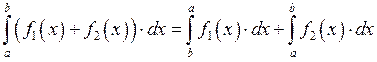
![]() Свойство линейности
Свойство линейности
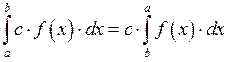
![]() Свойство монотонности
Свойство монотонности
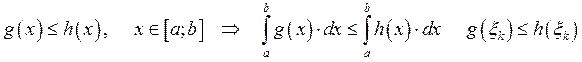
![]() Свойство аддитивности
интеграла Римана
Свойство аддитивности
интеграла Римана
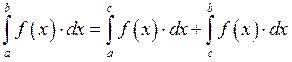
![]() Оценка интеграла мо модулю
Оценка интеграла мо модулю
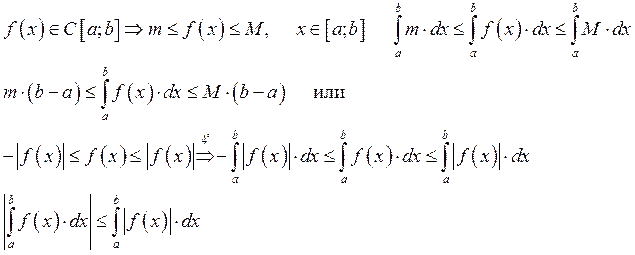
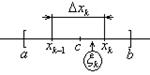
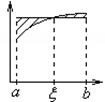
![]() Теорема о среднем
Теорема о среднем
![]()
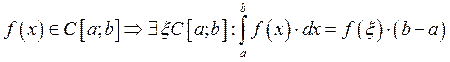
![]()
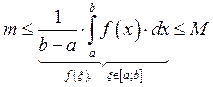
СДЕЛАТЬ ДОМА
1.11. Интеграл с переменным верхним пределом.
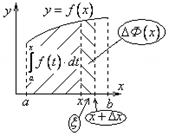
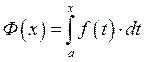
![]()
![]()
![]() интегрируема (ограничена) на
интегрируема (ограничена) на ![]() непрерывна на
непрерывна на ![]()
СДЕЛАТЬ ДОМА
![]()
![]()
![]() непрерывна на
непрерывна на ![]()
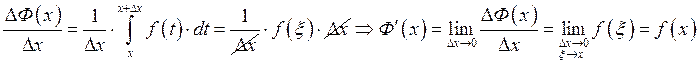
Следствие: Формула Ньютона-Лейбница.
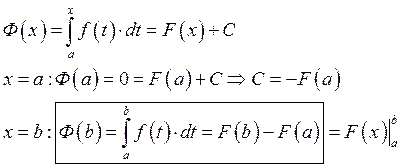
Пример: 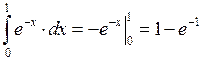
1.12. Методы интегрирования при вычислении определённого интеграла.
А) Замена переменной.
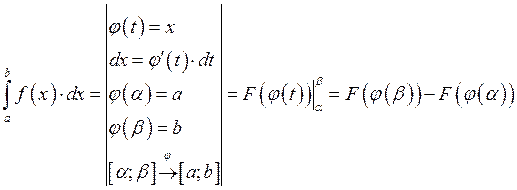
Пример: 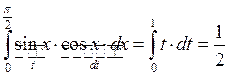
Б) Интегрирование по частям.
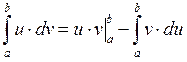
Пример:
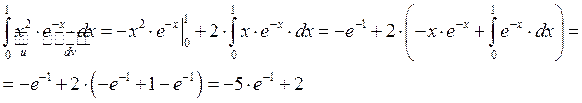
1.13. Вычисление площадей.
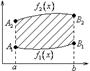 А)
А)
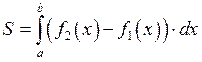
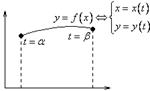 Б)
Б)
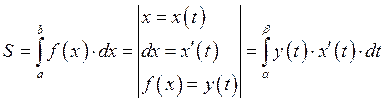
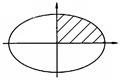 Пример:
Пример:
Элипс:
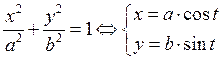
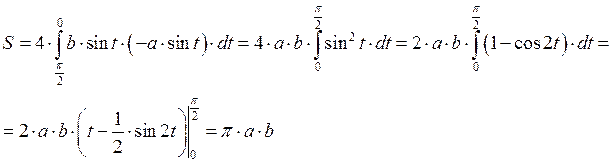
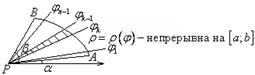 В) Площадь криволинейного сектора.
В) Площадь криволинейного сектора.
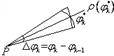
или
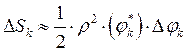
![]()
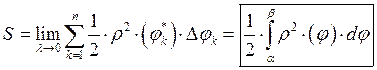
Пример:
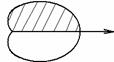
![]()
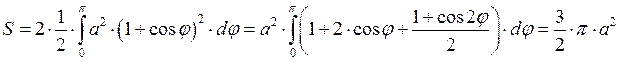
1.14. Вычисление объёмов.
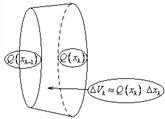
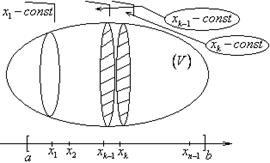 А) Метод паралельных сечений.
А) Метод паралельных сечений.
![]()
![]()
![]() непреравна на
непреравна на ![]()
![]()
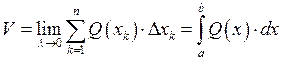
Пример: Объём 3-х осного элипсоида.
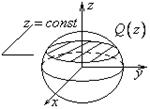
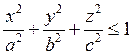
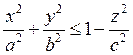
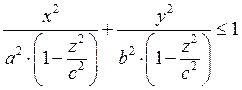
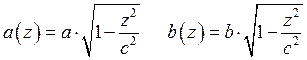
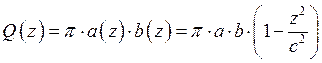
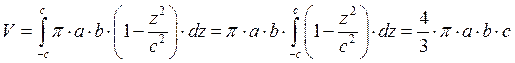
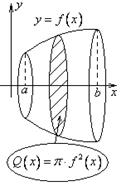 Б) Объём тела вращения.
Б) Объём тела вращения.
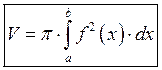
Пример:
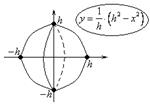 Лимон Ковалье.
Лимон Ковалье.
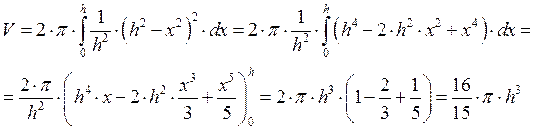
Интеграл от симметричных функций.
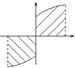
![]() Чётная:
Чётная: 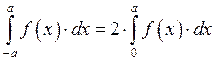
Нечётная: 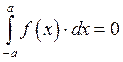
1.15. Длина кривой. (Длина линии).
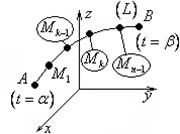
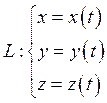
![]()
![]()

![]()
![]() длина отрезка.
длина отрезка. ![]()
![]()
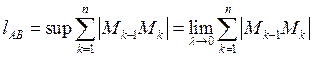
Достаточное условие спрямляемости кривой,
![]() непрерывна на
непрерывна на ![]()

![]()
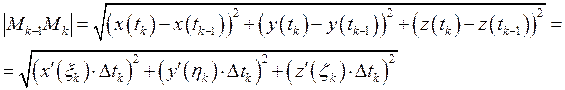
По теореме Лагранжа следует: ![]()
Тогда: ![]()
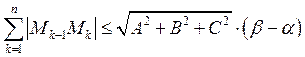 , Что и требовалось доказать.
, Что и требовалось доказать.
![]()
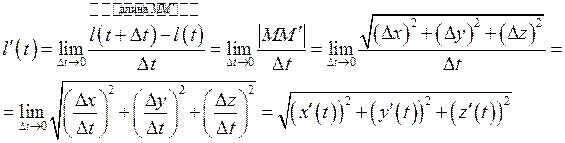
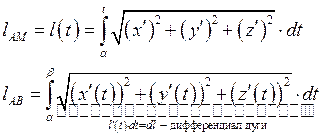
 Пример:
Пример:
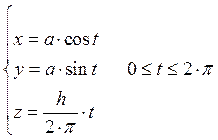
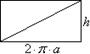
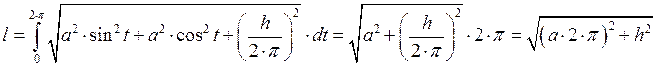
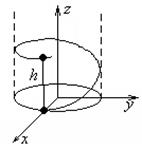
А) Плоская кривая.
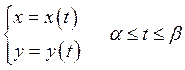

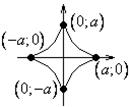 Пример:
Пример:
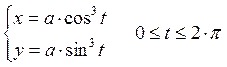
Астроида
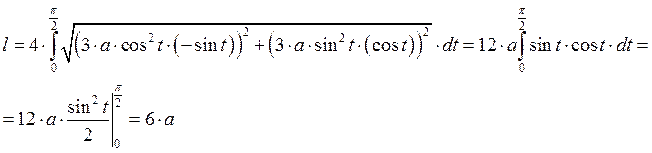
Б) Задание кривой.
![]()
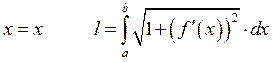
Пример: ![]()
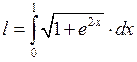
СДЕЛАТЬ ДОМА
В) Длина кривой в полярных координатах.
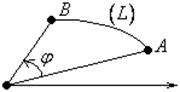
![]()
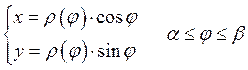
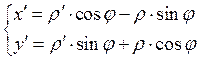
![]()
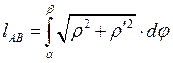
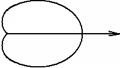 Пример:
Пример:
![]()
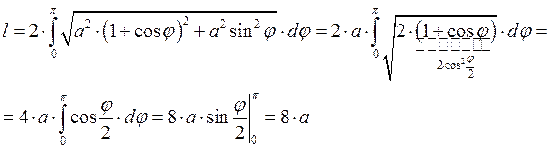
1.16. Несобственный интеграл I-ого рода.
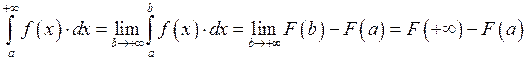
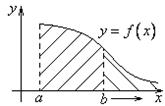 Если существует конечное значение
Если существует конечное значение ![]() ,
то интеграл сходится, иначе расходится.
,
то интеграл сходится, иначе расходится.
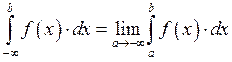
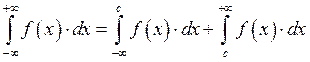
Пример 1:
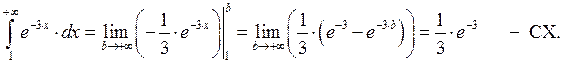
Пример 2:
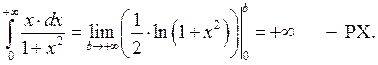
Пример 3:
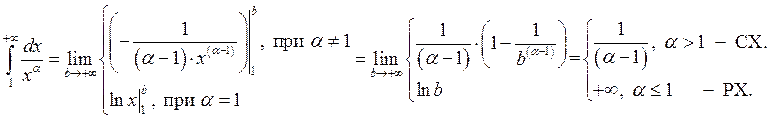
Пример 4:
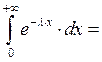 СДЕЛАТЬ
ДОМА
СДЕЛАТЬ
ДОМА 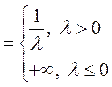
Простейшие свойства несобственного интеграла I-ого рода.
![]() Свойство линейности.
Свойство линейности.
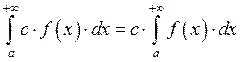
![]() Свойство линейности.
Свойство линейности.
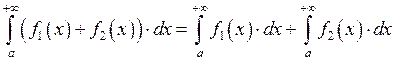
Эти интегралы должны сходиться.
Несобственные интегралы I-ого рода от неотрицательных функций.
![]()
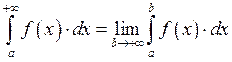
Для того чтобы интеграл сходился необходимо, чтобы 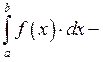 был ограниченным.
был ограниченным.
![]() ограничено
сверху.
ограничено
сверху.
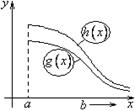
![]() (I-ая
теорема сравнения).
(I-ая
теорема сравнения).
![]()
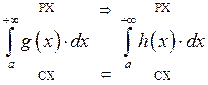
![]() (II-ая
теорема сравнения).
(II-ая
теорема сравнения).
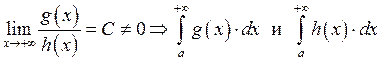
Если сходится один, то сходится и другой.
Пример 1:
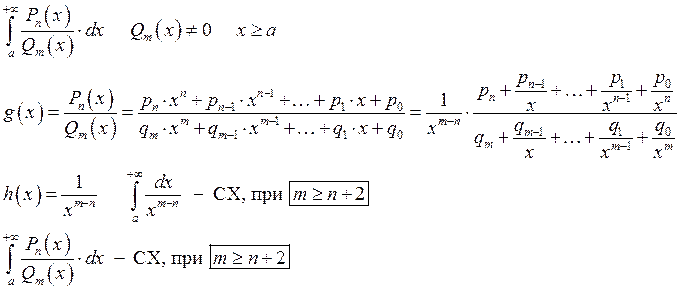
Пример 2:
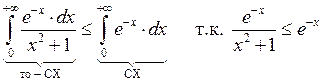
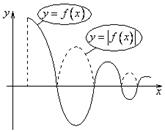
Абсолютная сходимость.
![]()
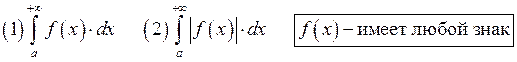
(Теорема о абсолютной сходимости).
![]()
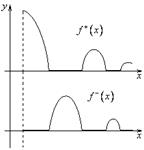
![]()
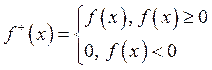
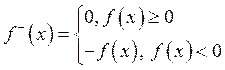
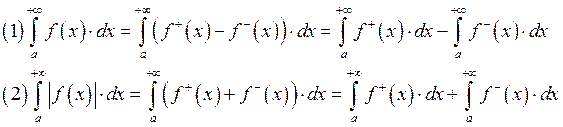
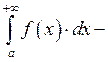 абсолютно
сходящийся, если
абсолютно
сходящийся, если 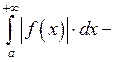 сходится.
сходится.
Если 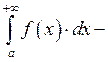 сходится,
а
сходится,
а 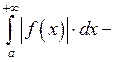 расходится, то
расходится, то 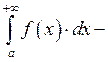 условно
сходящийся.
условно
сходящийся.
Главное значение несобственного интеграла I-ого рода.
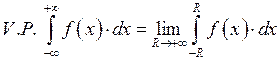
![]() Value principal
(главное значение).
Value principal
(главное значение).
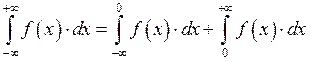
Пример:
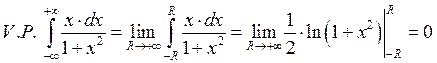
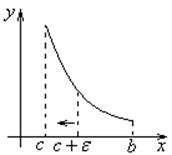
1.17. Несобственный интеграл II-ого рода.
![]() неограничен в окрестности точки
неограничен в окрестности точки ![]()
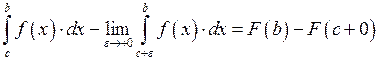
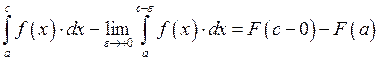
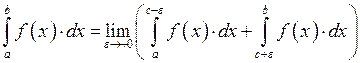
Пример:
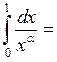 СДЕЛАТЬ
ДОМА
СДЕЛАТЬ
ДОМА 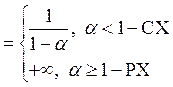
Несобственные интегралы II-ого рода от неотрицательных функций.
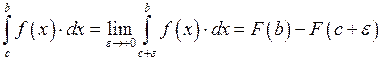
![]() (I-ая
теорема сравнения).
(I-ая
теорема сравнения).
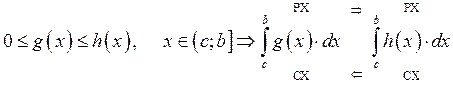
![]() (II-ая
теорема сравнения).
(II-ая
теорема сравнения).
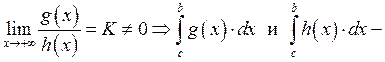 сходятся
и расходятся одновременно.
сходятся
и расходятся одновременно.
![]() (Теорема о абсолютной сходимости).
(Теорема о абсолютной сходимости).
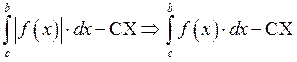
Пример 1:
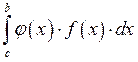
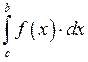
![]() непрерывна на
непрерывна на![]()
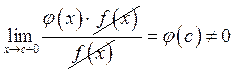
Пример 2:
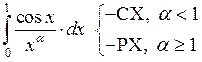
1.18. Интегралы, зависящие от параметра.
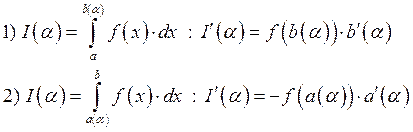
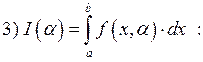 В ситуациях имеющих практическое
значение может быть вычислен по:
В ситуациях имеющих практическое
значение может быть вычислен по: 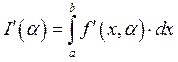
Пример:
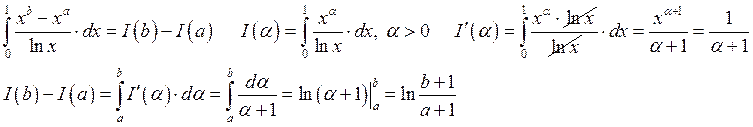
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.